2018-03-13 19:02:13
在图论中,网络流(英语:Network flow)是指在一个每条边都有容量(capacity)的有向图分配流,使一条边的流量不会超过它的容量。通常在运筹学中,有向图称为网络。顶点称为节点(node)而边称为弧(arc)。一道流必须匹配一个结点的进出的流量相同的限制,除非这是一个源点(source)──有较多向外的流,或是一个汇点(sink)──有较多向内的流。一个网络可以用来模拟道路系统的交通量、管中的液体、电路中的电流或类似一些东西在一个结点的网络中游动的任何事物。
一、最大流最小割定理
最大流最小割定理提供了对于一个网络流,从源点到目标点的最大的流量等于最小割的每一条边的和。
这个定理说明,当网络达到最大流时,会有一个割集,这个割集中的所有边都达到饱和状态。
这等价于在网络中再也找不到一个从s到t的增广路径。
因为只要能找到一条增广路径,这条增广路径肯定要经过最小割集中的一条边,否则这个割集就不能称之为割集了。
既然这个割集中所有的边都饱和了,因此也就不会存在这样的增广路径了。
这个定理的意义在于给我们指明了方向:
任何算法,只要最后能达到“再也找不到一条增广路径”,就可以说明这个算法最后达到了最大流。
二、最大流问题
在优化理论中,最大流问题涉及到在一个单源点、单汇点的网络流中找到一条最大的流。
最大流问题可以被看作是一个更复杂的网络流问题(如循环问题(circulation problem))的特殊情况,。s-t流(从源点s到汇点t)的最大值等于s-t割的最小容量,这被称为最大流最小割定理。
下面举例来说明这个问题:
问题描述:
给定一个有向图G=(V,E),把图中的边看作管道,每条边上有一个权值,表示该管道的流量上限。给定源点s和汇点t,现在假设在s处有一个水源,t处有一个蓄水池,问从s到t的最大水流量是多少。
这个问题有如下的一些限制:
- 容量限制:也就是在每条通路上的流量都不能超过其capacity。
- 平衡条件:除了源点和汇点,其他的点的流入量需要等于流出量。
- 反对称:v到u的净流量等于u到v的净流量的相反。
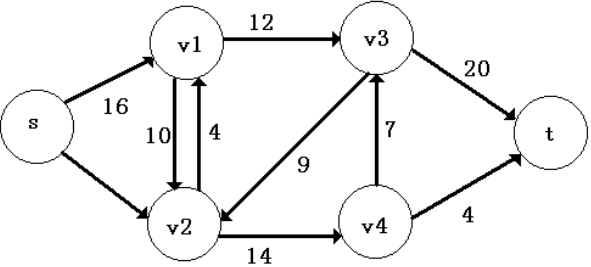
问题求解:
方法一、朴素dfs
一种非常朴素的思路是,使用dfs每次寻找s->t的一条通路,然后将这条路上的流量值定义为其中最小的容量值,完成这次运输后,将通路上的所有边的容量值减去流量值,开始下一次的寻找,直到没有通路,完成算法。
这个算法看上去是没有什么问题的,因为每次都在增加流量直到不能增加为止,可是真的是这样么?
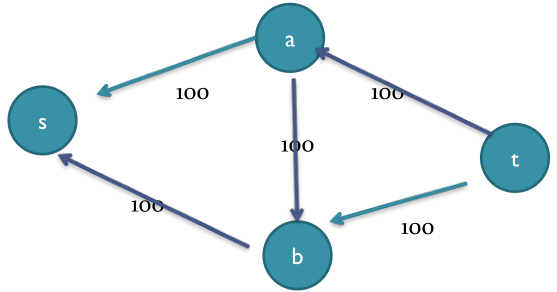
我们看下面的这个例子:

如果第一次dfs到的通路是s - > a - > b - > t,那么这次之后,网络中就再也没有从s - > t的通路了,按照算法的思路,这个网络的最大流就是100,然而,很明显的,这个网络的最大流是200。
因此,简单的使用dfs是不能很好的解决这个问题的,下面的Ford-Fulkerson算法解决了这个问题,而成为了网络流算法中的经典。
方法二、Ford-Fulkerson算法
在上面的例子中出错的原因是a - > b 的实际流量应该是0,但是我们过早的认为他们之间是有流量的,因此封锁了我们最大流继续增大的可能。
一个改进的思路:应能够修改已建立的流网络,使得“不合理”的流量被删掉。
一种实现:对上次dfs 时找到的流量路径上的边,添加一条“反向”边,反向边上的容量等于上次dfs 时找到的该边上的流量,然后再利用“反向”的容量和其他边上剩余的容量寻找路径。
下面我们重新对上面的例子进行分析:
1、第一次dfs依然是s - > a - > b - > t,与上次不同的是,这次我们会添加上反向边。
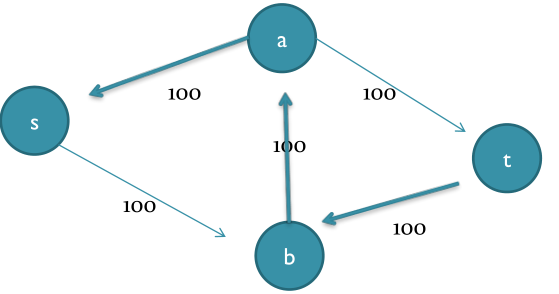
2、继续在新图上找可能通路,我们这次可以找到另一条流量为100的通路s - > b - > a - > t,从宏观上来看,反向边起到了“取消流”的功能,也可以看成是两条通路的合并。 
3、对第二次找到的路径添加反向边,我们发现图中已经没有从s - > t的通路了,于是该网络的最大流就是200。
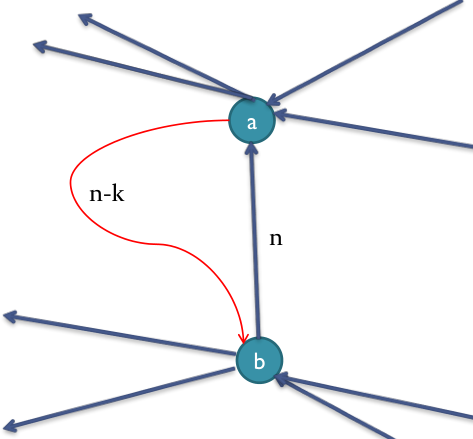
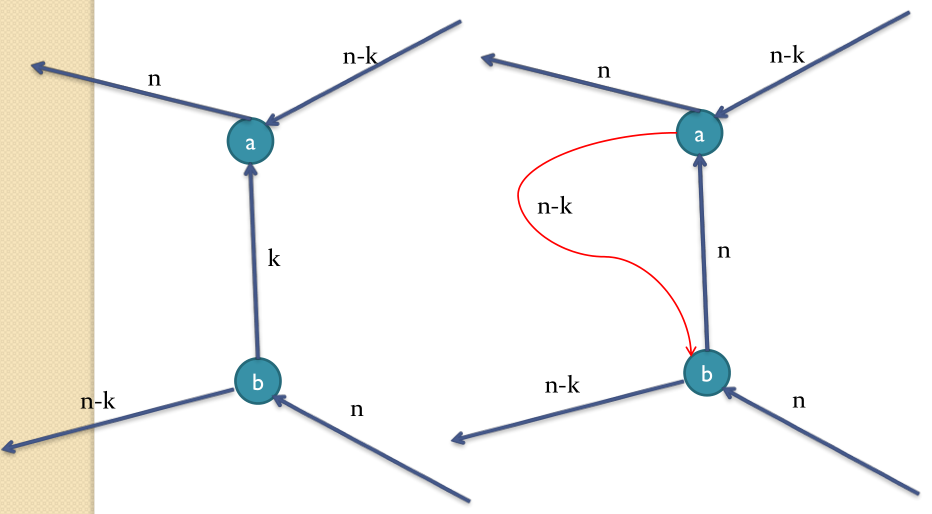
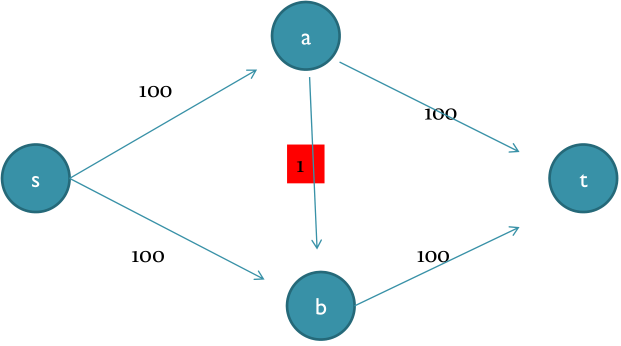
添加反向边的证明:
构建残余网络时添加反向边a->b,容量是n,增广的时候发现了流量n-k,即新增了n-k的流量。这n-k的流量,从a进,b出,最终流到汇。
现要证明这2n-k的从流量,在原图上确实是可以从源流到汇的。
在原图上可以如下分配流量,则能有2n-k从源流到汇点:
三、Ford-Fulkerson算法
Ford-Fulkerson算法:求最大流的过程,就是不断找到一条源到汇的路径,然后构建残余网络,再在残余网络上寻找新的路径,使 总流量增加,然后形成新的残余网络,再寻找新路径….. 直到某个残余网络上找不到从源到汇的路径为止,最大流就算出来了。
残余网络 (Residual Network):在一个网络流图上,找到一条源到汇的路径(即找到了一个流量)后,对路径上所有的边,其容量都减去此次找到的流量,对路径上所有的边,都添加一条反向边,其容量也等于此次找到的流量,这样得到的新图,就称为原图的“残余网络”。
增广路径: 每次寻找新流量并构造新残余网络的过程,就叫做寻找流量的“增广路径”,也叫“增广”。
算法时间复杂度分析:现在假设每条边 的容量都是整数,这个算法每次都能将流至少增加1。由于整个网络的流量最多不超过 图中所有的边的容量和C,从而算法会结束现在来看复杂度找增广路径的算法可以用dfs,复杂度为O(V + E)。dfs最多运行C次所以时间复杂度为C*(V + E) =C * V ^ 2。
四、Edmonds-Karp算法
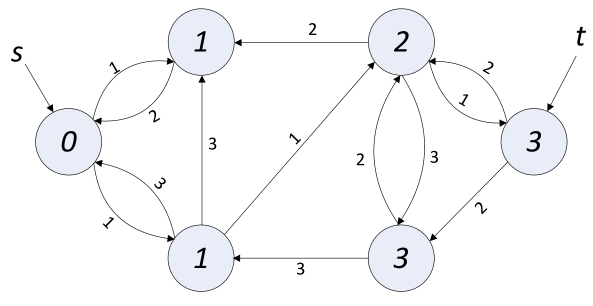
这个算法实现很简单但是注意到在图中C可能很大很大,比如说下面这张图,如果运气不好 这种图会让你的程序执行200次dfs,虽然实际上最少只要2次我们就能得到最大流。为了避免这个问题,我们每次在寻找增广路径的时候都按照bfs进行寻找,而不是按照dfs进行寻找,这就是Edmonds-Karp最短增广路算法。
时间复杂度:已经证明这种算法的复杂度上限为O(V*E^2)。
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
// POJ 1273
public class EdmondsKarp {
static int[][] G = new int[300][300];
static boolean[] visited = new boolean[300];
static int[] pre = new int[300];
static int v;
static int e;
static int augmentRoute() {
Arrays.fill(visited, false);
Arrays.fill(pre, 0);
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(1);
boolean flag = false;
while (!queue.isEmpty()) {
int cur = queue.poll();
visited[cur] = true;
for (int i = 1; i <= v; i++) {
if (i == cur) continue;
if (G[cur][i] != 0 && !visited[i]) {
pre[i] = cur;
if (i == v) {
flag = true;
queue.clear();
break;
}
else queue.add(i);
}
}
}
if (!flag) return 0;
int minFlow = Integer.MAX_VALUE;
int tmp = v;
while (pre[tmp] != 0) {
minFlow = Math.min(minFlow, G[pre[tmp]][tmp]);
tmp = pre[tmp];
}
tmp = v;
while (pre[tmp] != 0) {
G[pre[tmp]][tmp] -= minFlow;
G[tmp][pre[tmp]] += minFlow;
tmp = pre[tmp];
}
return minFlow;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int res = 0;
for (int i = 0; i < G.length; i++) {
Arrays.fill(G[i], 0);
}
e = sc.nextInt();
v = sc.nextInt();
int s, t, c;
for (int i = 0; i < e; i++) {
s = sc.nextInt();
t = sc.nextInt();
c = sc.nextInt();
G[s][t] += c;
}
int aug;
while ((aug = augmentRoute()) != 0) {
res += aug;
}
System.out.println(res);
}
}
}
五、Dinic算法
Edmonds-Karp已经是一种很不错的改进方案了,但是每次生成一条增广路径都需要对s到t调用BFS,如果能在一次增广的过程中,寻找到多条增广路径,就可以进一步提高算法的运行效率。
Dinic算法就是使用了BFS + DFS达到了以上的思路,完成了算法复杂度的进一步下降。
时间复杂度:O(V^2 * E)
算法流程:
1、使用BFS对残余网络进行分层,在分层时,只要进行到汇点的层次数被算出即可停止,因为按照该DFS的规则,和汇点同层或更下一层的节点,是不可能走到汇点的。

2、分完层后,从源点开始,用DFS从前一层向后一层反复寻找增广路(即要求DFS的每一步都必须要走到下一层的节点)。
3、DFS过程中,要是碰到了汇点,则说明找到了一条增广路径。此时要增加总流量的值,消减路径上各边的容量,并添加反向边,即所谓的进行增广。
4、DFS找到一条增广路径后,并不立即结束,而是回溯后继续DFS寻找下一个增广路径。回溯到的结点满足以下的条件:
1) DFS搜索树的树边(u,v)上的容量已经变成0。即刚刚找到的增广路径上所增加的流量,等于(u,v)本次增广前的容量。(DFS的过程中,是从u走到更下层的v的)
2) u是满足条件 1)的最上层的节点。
5、如果回溯到源点而且无法继续往下走了,DFS结束。因此,一次DFS过程中,可以找到多条增广路径。
6、DFS结束后,对残余网络再次进行分层,然后再进行DFS当残余网络的分层操作无法算出汇点的层次(即BFS到达不了汇点)时,算法结束,最大流求出。
一般用栈实现DFS,这样就能从栈中提取出增广路径。
// POJ 1273
public class Dinic { static int[][] G = new int[300][300]; static boolean[] visited = new boolean[300]; static int[] layer = new int[300]; static int v; static int e; static boolean countLayer() { int depth = 0; Arrays.fill(layer, -1); layer[1] = 0; Queue<Integer> queue = new LinkedList<Integer>(); queue.add(1); while (!queue.isEmpty()) { int cur = queue.poll(); for (int i = 1; i <= v; i++) { if (G[cur][i] > 0 && layer[i] == -1) { layer[i] = layer[cur] + 1; if (i == v) { queue.clear(); return true; } queue.add(i); } } } return false; } static int dinic() { int res = 0; List<Integer> stack = new ArrayList<Integer>(); while (countLayer()) { stack.add(1); Arrays.fill(visited, false); visited[1] = true; while (!stack.isEmpty()) { int cur = stack.get(stack.size() - 1); if (cur == v) { int minFlow = Integer.MAX_VALUE; int minS = Integer.MAX_VALUE; for (int i = 1; i < stack.size(); i++) { int tmps = stack.get(i - 1); int tmpe = stack.get(i); if (minFlow > G[tmps][tmpe]) { minFlow = G[tmps][tmpe]; minS = tmps; } } // 生成残余网络 for (int i = 1; i < stack.size(); i++) { int tmps = stack.get(i - 1); int tmpe = stack.get(i); G[tmps][tmpe] -= minFlow; G[tmpe][tmps] += minFlow; } // 退栈到minS while (!stack.isEmpty() && stack.get(stack.size() - 1) != minS) { stack.remove(stack.size() - 1); } res += minFlow; } else { int i; for (i = 1; i <= v; i++) { if (G[cur][i] > 0 && layer[i] == layer[cur] + 1 && !visited[i]) { visited[i] = true; stack.add(i); break; } } if (i > v) { stack.remove(stack.size() - 1); } } } } return res; } public static void main(String[] args) { Scanner sc = new Scanner(System.in); while (sc.hasNext()) { for (int i = 0; i < G.length; i++) { Arrays.fill(G[i], 0); } e = sc.nextInt(); v = sc.nextInt(); int s, t, c; for (int i = 0; i < e; i++) { s = sc.nextInt(); t = sc.nextInt(); c = sc.nextInt(); G[s][t] += c; } System.out.println(dinic()); } } }
六、最小费用最大流
问题描述:
设有一个网络图 G(V,E) , V={s,a,b,c,…,s ’},E 中的每条边 (i,j) 对应一个容量 c(i,j) 与输送单位流量所需费用a(i,j) 。如有一个运输方案(可行流),流量为 f(i, j) ,则最小费用最大流问题就是这样一个求极值问题:
![]()
其中 F 为 G 的最大流的集合,即在最大流中寻找一个费用最小的最大流。
算法流程:

反复用spfa算法做源到汇的最短路进行增广,边权值为边上单位费用。反向边上的单位费用是负的。直到无法增广,即为找到最小费用最大流。
成立原因:每次增广时,每增加1个流量,所增加的费用都是最小的。