动态规划题目特点
1.计数
有多少种方式走到右下角
有多少种方法选出K个数使得和是sum
2.求最大最小值
从左上角到右下角路径的最大数字和
最长上升子序列长度
3.求存在性
取石子游戏,先手是否取胜
能不能选出k个数使得和是sum
例题:
你有三种硬币,面值分别是2元、5元和7元,每种硬币都足够多。
买一本书要27元,如何用最少的硬币组合正好付清,不需要对方找钱。
动态规划组成部分一:确定状态
状态在动态规划中的作用属于定海神针
简单的说,解动态规划的时候需要开一个数组,数组的每一个元素f[i]或者f[i][j]代表什么。这类似于接数学题中,X,Y,Z代表什么。
由于刚开始拿到题目时,我们往往不知道这些数组中的元素代表什么,所以就要确定状态。
确定状态需要两个意识:
-最后一步
-子问题
最后一步:我们肯定知道我们的目标是什么,我们把实现我们的目标的策略称为最优策略。而最后一步就是我们最优策略中的最后一步决策。
在本题中,我们的目标是求一种硬币数量最少的硬币组合。我们把这种硬币组合称为最优策略。我们不知道最优策略,也就是这个组合是什么样子的,但是最优策略一定是K枚硬币a1, a2, ....., ak面值加起来是27。最后一步就是最后的一枚硬币ak.
那么除去最后最后一步硬币ak,前面的硬币面值加起来就是27-ak。

关键点1
我们不关心前面的k-1枚硬币是怎么拼出27-ak的(可能有1种拼法,也可能有100种拼法),而且现在我们甚至还不知道ak和k,但是我们确定前面的硬币拼出了27-ak。
关键点2
因为这个是最优策略,所以拼出27-ak的硬币数也一定要最少,否则就不是最优策略了。
可以用反证法来证明。设现在拼出27-ak的硬币数为a。如果存在一种硬币组合方式使得拼出27-ak的硬币数更少,设硬币数为b。所以由b < a。则可得,我们的最优策略的总的硬币数为a+1,前面假设的组合硬币数为b+1。显然可得 a+1 >b + 1。这就与我们的最有策略相矛盾。所以拼出27-ak的硬币数也一定是最少的。否则就不再是最优策略。
也就是,最优策略中把最后一步去掉之后拼出27-ak的组合仍然是最优的。
子问题
所以我们就要求:最少用多少枚硬币可以拼出27-ak
原问题是最少用多少枚硬币拼出27,现在我们将原问题转换成了一个子问题,而且规模更小:27-ak。
为了简化定义,我们设状态f(x)=最少用多少枚硬币可以拼出X。
那么我们原来是要求f(27),现在则是转换成为了f(27-ak)。
但是现在我们还不知道最后那枚硬币ak是多少,但是最后最后那枚硬币只可能是2、5或7.
如果ak是2, 那么f(27)应该是f(27-2) +1
如果ak是5, 那么f(27)应该是f(27-5) +1
如果ak是7, 那么f(27)应该是f(27-7) +1
除此之外没有其他的可能了
需要求最少的硬币数。所以

使用递归方式来求解此问题,程序如下
//递归解法 //f(x)是最少用多少枚硬币拼出x //返回值res就是拼出x用的最少硬币数 int f(int x){ //0元钱只要0枚硬币 if (x == 0) return 0; //把结果res初始化为无穷大。发现有比res小的值则进行进一步更新 int res = MAX_VALUE; //如果要拼凑出3块钱,也就是f(3),我们肯定不会使用5块钱来拼凑,只会用小于3块钱的来拼凑 //注意,这里的if语句是平行关系,并不会上面的满足条件后就跳过后面的if语句。 //而是从上往下依次执行.当x>=7时,实现res = min(f(x - 2) + 1, f(x - 5) + 1, f(x - 7) + 1, res) //最后一枚硬币是2元 if(x >= 2) res = Math.min(f(x - 2) + 1, res); //最后一枚硬币是5元 if(x >= 5) res = Math.min(f(x - 5) + 1, res); //最后一枚硬币是7元 if(x >= 7) res = Math.min(f(x - 7) + 1, res); return res; }
递归解法中的问题
我们在求解f(27)时,程序要去递归f(25),f(22),f(20)。然后再进一步求解f(25)时就会进一步递归求解,从而形成下面的树
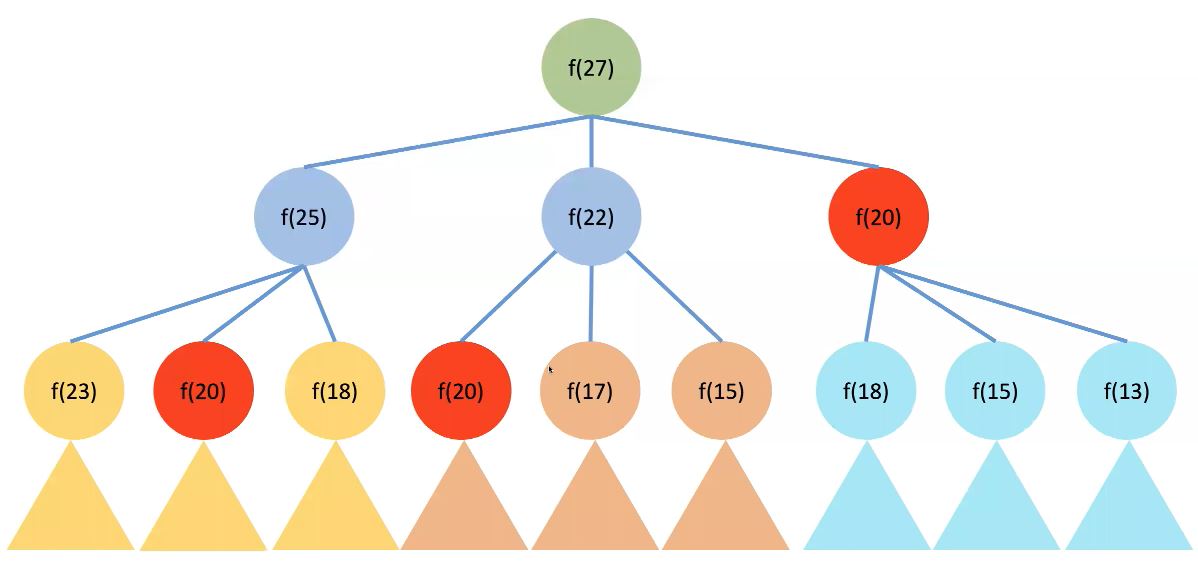
我们会发现,出现大量的重复计算。如f(20)出现了3次,这里不是仅仅f(20)出现了3次,而是计算f(20)下面的递归,就是以f(20)为根节点的整棵树都计算了3次。当递归数值较大的时候计算量就是天文数字。所以递归解法做了很多的重复计算,使得效率低下。
那么动态规划是如何来实现呢?它是通过将计算结果保存下来,并改变计算顺序来实现的。
动态规划组成部分二:转移方程
设状态f[x] = 最少用多少枚硬币拼出x
那么对于任意x, 均有
f[x] = min{f[x - 2] + 1, f[x - 5] + 1, f[x - 7] + 1}
动态规划组成部分三:初始条件和边界情况
f[x] = min{f[x - 2] + 1, f[x - 5] + 1, f[x - 7] + 1}
两个问题:
一:x - 2, x - 5, 或者x - 7小于0怎么办?
二:什么时候停下来?
如果不能拼出Y,就定义f[Y] = 正无穷
例如f[-1] = f[-2] = ... = 正无穷
对于1块钱,我们也是无法拼出来的,所以f[1] = min{f[-1] + 1, f[-4] + 1, f[-6] + 1} = 正无穷,表示拼不出来1。
初始条件:f[0] = 0。0块钱用0个硬币来拼凑。这是一个很经常用的初始条件
初始条件其实是用状态方程算不出来,但是需要的条件,这就需要手工来定义。
动态规划组成部分四:计算顺序
拼出x所需要的最少硬币数:f[x] = min{f[x - 2] + 1, f[x - 5] + 1, f[x - 7] + 1}
初始条件:f[0] = 0
然后计算f[1], f[2], ..., f[27]
大部分动态规划的计算顺序都是从小到大,二维的计算则是从上到下,从左到右
我们计算顺序的确定只有一个原则,就是当计算方程左边的f[x]时,方程右边的式子中的整式都已经计算过了,或者说都是已知量了。在本题中,我们计算式f[x] = min{f[x - 2] + 1, f[x - 5] + 1, f[x - 7] + 1},要计算方程左边的f[x], 等式右边的f[x - 2] , f[x - 5] , f[x - 7] 都已经有计算结果了。所以计算顺序是从小到大。
则本题的计算顺序为
计算f[1], f[1]无法拼凑出来

计算f[2]
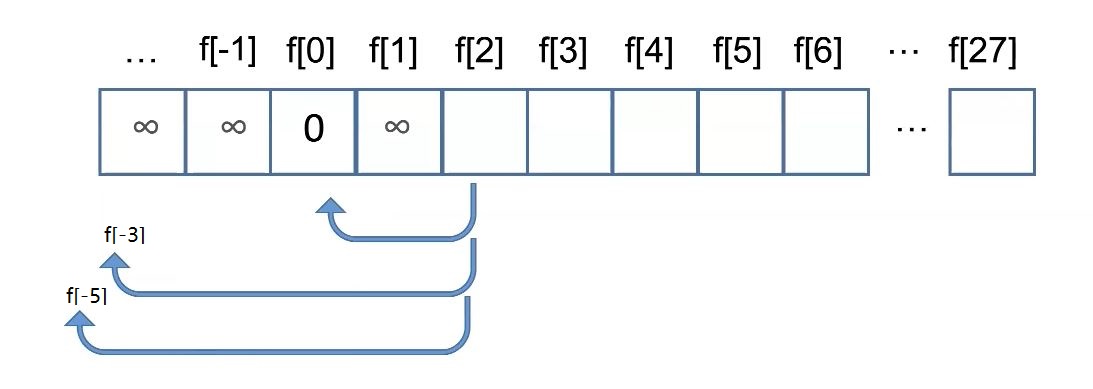
f[3]使用了f[1], f[-2], f[-4]拼不出来
f[4]使用了f[2], f[-1], f[-3],通过两个f[2]拼凑出来

最后计算出f[27]

每一步都尝试计算三种硬币,一共27步(计算f(0), f(1), ....., f(27))。
与递归算法相比,没有任何重复计算
算法时间复杂度(即需要进行的步数):27 * 3
小结
求最值型动态规划
动态规划组成部分
1.确定状态
最后一步(最优策略中使用的最后一枚硬币ak)
化成子问题(最少的硬币拼出更小的面值27 - ak)
2.转移方程
f[x] = min{f[x - 2] + 1, f[x - 5] + 1, f[x - 7] + 1}
3.初始条件和边界情况
f[0] = 0,如果不能拼出Y,则f[Y] = 正无穷
初始条件其实是用状态方程算不出来,但是需要的条件,这就需要手工来定义。并且意义很清晰,能够明确得出
4.计算顺序
我们计算顺序的确定只有一个原则,就是当计算方程左边的f[x]时,方程右边的式子中的整式都已经计算过了,或者说都是已知量了。
大部分都是从小到大计算,在二维中则多是从上到下,从左到右计算。
消除冗余,加速计算。
本题代码
public class Solution{ public: //硬币放在数组A里面, //M代表要拼出的钱数 int coinchange(int A[], int M){ //在c++语言中,数组下标从0开始,我们要计算到M,那么开辟的内存空间大小应该是M+1 int f[M + 1]; //硬币种类的数量 int n = sizeof(A) / sizeof(int); //定义一个非常大的不可能的数当作无穷大 very_large = 100000; //initialization //指定初始条件 f[0] = 0; int i, j; //f[1], f[2], ... , f[27] for(i = 1; i <= M;++i) { //把初始值设置为无穷大,有情况比它好就去更改 f[i] = very_large; //这里是最后一步。也就是我们要拼出i块钱,最后一枚硬币A[j]的值 //f[i] = min(f[i - A[0]] + 1, ..., f[i - A[n - 1]] + 1) for(j = 0; j < n; j++) { //由于i - A[j]可能是负数 //在数学上,无穷大加一还是无穷大,但是在编程中,则就会出现溢出问题 //所以如果是其它语言,在if语句内还要加个判断f[i - A[j]] != Interger.MAX_VALUE if(i >= A[j]) { f[i] = min(f[i - A[j]] + 1, f[i]); } } } if(f[M] >= 99000) f[M] = -1; return f[M] } }
(二)
题意:
给定m行n列的网格,有一个机器人从左上角(0,0)出发,每一步可以向下或者向右走一步,问有多少种不同的方式走到右下角。
注意:不管什么样的动态规划都可以使用前面介绍的四个部分来求解。
动态规划组成部分一:确定状态
最后一步:无论机器人用何种方式到大右下角,总有最后挪动的一步:向下 或者向右。
右下角坐标设为(m - 1, n - 1)
那么前一步机器人一定是在(m - 2, n - 1)或者在(m - 1, n - 2)
那么,如果机器人右x中方式从左上角走到(m - 2, n - 1),有y种方式走到(m - 1, n - 2), 则机器人有x + y 种方式走到(m - 1, n - 1).
这里为什么是x + y呢?就是加法原理得到的。
问题转化为:机器人有多少种方式从左上角走到(m - 2, n - 1)和(m - 1, n - 2)
原题要求有多少种方式从左上角走到(m - 1, n - 1)
子问题
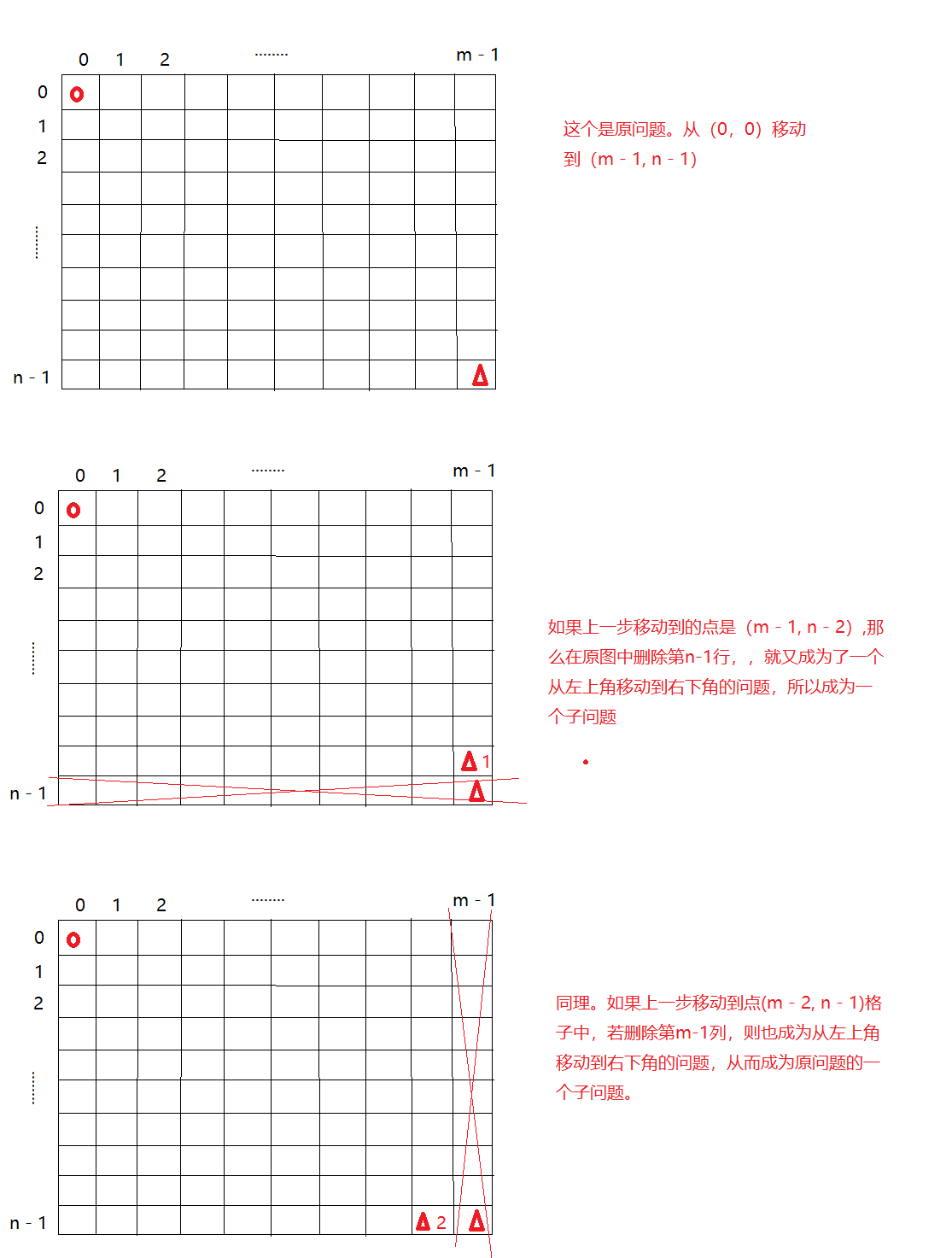
状态:设f[i][j]为机器人有多少种方式从左上角走到(i,j).。数组下标[i][j]就是网格(i,j)
注:至于数组为几维,则应按照原问题种有几个变量来设置。原问题中有几个变量,则设置为几维。在本题中有m-1, n-1两个变量,则开二维数组。
动态规划组成部分二:转移方程

动态规划组成部分三:初始条件和边界情况
初始条件:f[0][0] = 1, 因为机器人只有一种方式到左上角。
边界情况:i = 0或j = 0时,则前一步只能由一个方向过来,所以f[i][j] = 1
动态规划组成部分四:计算顺序
f[0][0] = 1
计算第0行: f[0][0], f[0][1], ... , f[0][n-1]
计算第1行: f[1][0], f[1][1], ... , f[1][n-1]
.....
计算第m - 1行: f[m - 1][0], f[m - 1][1], ... , f[m - 1][n-1]
这样的计算顺序是为了保证在计算(i,j)格子时,前面的问题都已经计算过。
答案是f[m - 1][n - 1]
时间复杂度(计算步数):O(MN),空间复杂度(数组大小):O(MN)
本题代码
class Solution{ public: int uniquePaths(int m, int n){ int f[][] = new int[m][n]; int i, j; for(i = 0; i < m; i++){ //row: up to down for(j = 0; j < n; j++){ //column: left to right if(i == 0 || j == 0) { //这里也包含了初始条件f[0][0] = 1 f[i][j] = 1; } else { f[i][j] = f[i - 1][j] + f[i][j - 1]; } } } return f[m - 1][n - 1]; } }
(三):存在型动态规划
有n块石头分别摆在x轴的0, 1, ... , n-1位置,如果一只青蛙在石头0,想要跳到石头n-1, 如果青蛙在第i块石头,它最多可以向右跳跃距离ai
问题:青蛙能否跳到石头n - 1
例子:输入:a = [2, 3, 1, 1, 4] 输出:True 输入:a = [3, 2, 1, 0, 4] 输出:False
组成部分一:确定状态
最后一步:如果青蛙能够到最后一块石头n-1, 我们考虑他的最后一步
这一步时从石头i跳过来, i < n - 1
这需要同时满足两个条件:
青蛙可以跳到石头i
最后一步不超过跳跃的最大距离: n - 1 - i <= ai
两个条件中第二个条件很容易判断。那么剩下的就是第一个条件:我们需要知道青蛙能不能跳到石头i(i < n-1)
而我们原来要求青蛙能不能跳到石头n - 1。这就成为一个子问题
状态:设f[j]表示青蛙能不能跳到石头j
组成部分二:转移方程
设f[j]表示青蛙能不能跳到石头j
f[j] = ORo<=i<j(f[i] AND i + a[i] > = j)
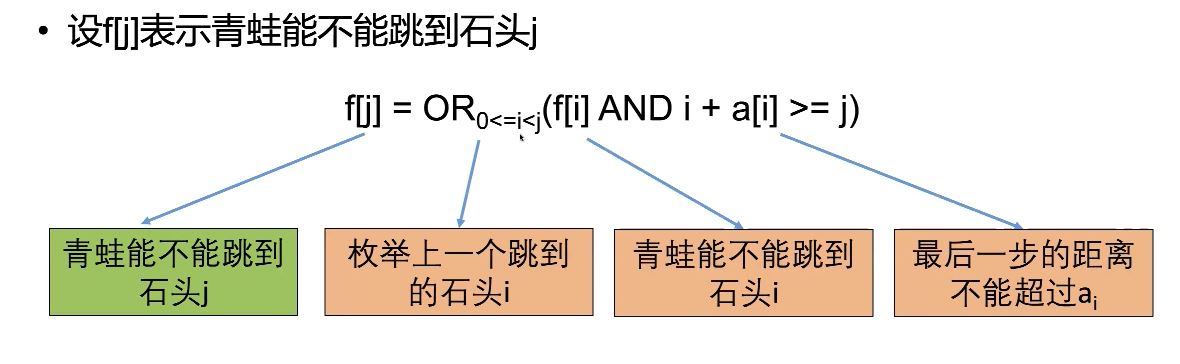
式中:OR表示进行for循环的时候只要有一个满足,就输出True,否则就输出False
组成部分三:初始条件和边界情况
设f[j]表示青蛙能不能跳到石头j
初始条件: f[0] = True, 因为青蛙一开始就在石头0
没有边界情况
计算顺序
设f[j]表示青蛙能不能跳到石头j
f[j] = ORo<=i<j(f[i] AND i + a[i] > = j)
初始化f[0] = True
计算f[1], f[2], ... , f[n - 1]
答案是f[n - 1]
class Solution{ public: boolean canjump(int A[]){ int n = sizeof(A) / sizeof(int); bool f[] = new bool[n]; f[0] = true; for(int j = 1; j < n; j++) { f[j] = false; //previous stone i //last jump is from i to j for(int i = 0; i < j; i++) { if(f[i] && i + A[i] >= j) { f[j] = true; break; } } } return f[n - 1] } }
(三)
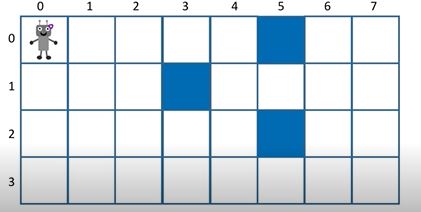
给定m行n列的网格,有一个机器人从左上角(0,0)出发,每一步可以向下或者想右走一步
网格中有一些障碍,机器人不能通过障碍
问有多少种不同的方式走到右下角
组成部分一:确定状态
机器人最后到达右下角(m - 1, n - 1)处,那么上个位置一定是在(m - 2, n - 1)或者(m - 1, n - 2)处。那么机器人到达右下角(m - 1, n - 1)的方式数量为到达(m - 2, n - 1)方式数量和到达(m - 1, n - 2)的方式数量之和。
原问题为:有多少种不同方式到达右下角
子问题为:有多少种方式到达位置(m - 2, n - 1)和位置(m - 1, n - 2)
组成部分二:状态方程
设f[i][j]为走到网格[i][j]处的方式数目。那么有f(m-1)(n-1)为到达位置(m - 1, n - 1)处的方式数量,那么到达(m - 2, n - 1)和(m - 1, n - 2)处的方式数量分别为f(m - 2)(n - 1)和f(m - 1)( n -2)
则状态方程为
f(i)(j) = f(i-1)(j) + f(i)(j-1)
组成部分三:初始条件和边界情况
当机器人位于点(0, 0 )处时,方式数数目为1。也就是机器人只有一种方式到达点(0,0),即f(0)(0) = 1
如果左上角和右下角有障碍,那么机器人永远无法到达,直接输出零
如果(i, j)处右障碍,则f[i][j] = 0,表示机器人无法到达此网格。
那么转移方程为

组成部分四:计算顺序
计算顺序按照从上到下,从左到右的顺序计算进行
class Solution{ public: int uniquepathswithobstacles(int A[][]) { if(A == NULL) { return 0; } int m = sizeof(A) / sizeof(A[0]); int n = sizeof(A[0]) / sizeof(A[0][0]); int f[][] = new int[m][n]; //做一个数组,下标为[i][j]的数组就是到达网格(i,j)处的方式数量。 //而且按照从上到下、从左到右的顺序计算,在进行计算(i,j)处的值时, //前j - 1行中的值全部计算完成,并且第j行前i-1个元素也已经计算完成。 //在计算第(i, j)处的值时可通过下标来使用计算过的值 for(int i = 0; i < m; i++) //行从左到右 { for(int j = 0; j < n; j++) //列从上到下 { //一票否决 //如果A[i][j] = 1表示此处有障碍,将f[i][j]置为0, //同时使用continue语句进行下轮循环进行下一个网格的计算 if(A[i][j] = 1) { f[i][j] = 0; continue; } if( i == 0 && j == 0) { f[i][j] = 0; continue; } //计算f[i][j]时先将f[i][j]置为0,然后再更新 f[i][j] = 0; //如果j=0,表示在第1列,不执行此语句。此时f[i][j] = 0 + f[i - 1][j] //如果i=0,表示在第1行,不执行下一个if语句,此时f[i][j] = f[i][j - 1] //如果i,j都大于0,则两个if语句同时执行,有f[i][j] = f[i][j - 1] + f[i - 1][j] if( j >0) { f[i][j] += f[i][j - 1]; } if( i > 0) { f[i][j] += f[i - 1][j]; } } } return f[m - 1][n - 1] } }
序列型规划
题目:
有一排N栋房子,每栋房子要漆成三种颜色中的一种:红、蓝、绿
任何两栋相邻的房子不能漆成同样的颜色
第i栋房子漆成红色、蓝色、绿色的花费分别时cost[i][0], cost[i][1], cost[i][2]
问最少需要花多少钱漆完这些房子
例子:
输入:
N = 3
cost = [[14, 2, 11], [11, 14, 5], [14, 3, 10]]
输出
-10 (第0栋房子蓝色,第1栋房子绿色,第2栋房子蓝色。 2 + 5 + 3 = 10)
为了便于理解,首先统一一下编号问题。
前N栋房子,是指房子共有N栋。是生活中习惯用语,前1栋就只有一栋,前2栋就是两栋房子。
而在java和c++中,数组下标是从0开始,所以房子N-1指的是第N栋房子(前N栋房子的最后一栋)。
综上所述:前N栋房子并且房子N-1是红色、蓝色、绿色的最小花费是指把前N栋房子都油漆完并且将第N栋(前N栋中的最后一栋)漆成红色、蓝色、绿色的花费。
组成部分一:确定状态
最优策略时花费最小的策略
在这里,第一栋房子编号为0,所以,前N栋房子的最后一栋房子编号为N-1。
最后一步:最优策略中房子N-1一定染成了红、蓝、绿中的一种。
但是相邻两栋房子不能漆成一种颜色
所以如果最优策略中房子N-1是红色,房子N-2只能是蓝色或绿色
所以如果最优策略中房子N-1是蓝色,房子N-2只能是红色或绿色
所以如果最优策略中房子N-1是绿色,房子N-2只能是蓝色或红色
如果直接套用以前的思路,记录油漆前N栋房子的最小花费
根据套路,也需要记录油漆前N-1栋房子的最小花费。
但是,前N-1栋房子的最小花费的最优策略中,不知道房子N-2(所有房子的倒数第二栋房子)是什么颜色,所以房子N-2有可能与房子N-1撞色。
为解决这个问题,所以有
不知道房子N-2是什么颜色,就把它记录下来。就是在状态里面增加一个维度,用来记录房子N-2的颜色。
分别记录油漆前N-1栋房子并且房子N-2(倒数第二栋)是红色、蓝色、绿色的最小花费。这个过程中,我们需要记录三个数值。就是我们记录油漆前N-1栋房子并且N-2栋房子是红色的最小花费、记录油漆前N-1栋房子并且N-2栋房子是蓝色的最小花费、记录油漆前N-1栋房子并且N-2栋房子是绿色的最小花费。
如果N-1栋房子是红色,那么在N-2栋房子我们只需看蓝色和绿色

如果N-1栋房子是蓝色,那么在N-2栋房子我们只需看红色和绿色
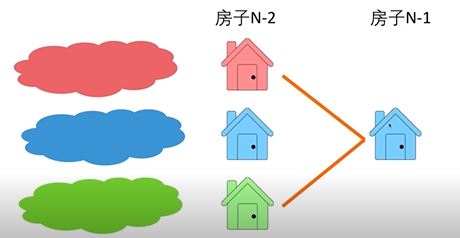
如果N-1栋房子是绿色,那么在N-2栋房子我们只需看红色和蓝色
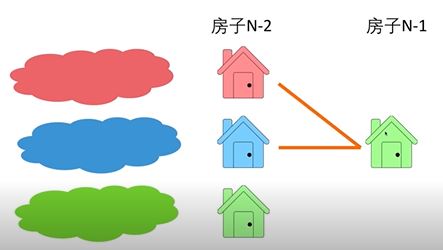
原问题:
求油漆前N栋房子且房子N-1(最后一栋)是红色、蓝色、绿色的最小花费。
子问题:
需要知道求油漆前N-1栋房子且房子N-2(倒数第二栋)是红色、蓝色、绿色的最小花费。
状态:
设油漆前i栋房子并且房子i-1是红色、蓝色、绿色的最小花费分别为f[i][0]、f[i][1]、f[i][2]
组成部分二:转移方程
设油漆前i栋房子并且房子i-1是红色、蓝色、绿色的最小花费分别为f[i][0]、f[i][1]、f[i][2]

以第一个式子为例来理解这个等式
下标的第二个维度是颜色的标记,0,1,2分别代表三种颜色。
f[i][0]表示油漆前i栋房子,并且i-1(前i栋房子的最后一栋)房子是颜色0的最小花费。
在这里,如果不考虑颜色冲突问题,那么油漆前i栋房子的费用等于油漆前i-1栋房子的费用加上油漆房子i-1的费用。
f[i-1][1]表示油漆前i-1栋房子,并且将房子i-2油漆成颜色1的最小花费
cost[i-1][0]:表示将房子i-1油漆成颜色0的费用。
整个式子的意思为:
油漆前i栋房子并且房子i-1油漆成颜色0的最小费用 = 油漆前i-1栋房子并且房子i-2油漆成颜色1的费用 + 将房子i-1油漆成颜色0的费用。
组成部分三:初始条件和边界情况
设油漆前i栋房子并且房子i-1是红色、蓝色、绿色的最小花费分别为f[i][0]、f[i][1]、f[i][2]
初始条件:f[0][0] = f[0][1] = f[0][2] = 0。即不油漆任何房子的花费。
无边界情况
组成部分四:计算顺序
设油漆前i栋房子并且房子i-1是红色、蓝色、绿色的最小花费分别为f[i][0]、f[i][1]、f[i][2]
初始化f[0][0]、f[0][1]、f[0][2]
计算f[1][0]、f[1][1]、f[1][2]
.。。。。
计算f[N][0]、f[N][1]、f[N][2]
答案是min{f[N][0]、f[N][1]、f[N][2]}, 时间复杂度O(N), 空间复杂度O(N)
在下面代码中设计最小值函数在运行时需要进行重新书写
class solution{ public: int minCost(int C[][]) { int n = sizeof(C) / sizeof(C[0]); if(n == 0) { return 0; } //这里一定要开n+1个空间 //因为除了存储1,... , N栋房子的花费,还要存储0栋房子时的花费 int f[][] = new int[n + 1][3]; //初始化,油漆0栋房子的最小花费 f[0][0] = 0; f[0][1] = 0; f[0][2] = 0; for(int i = 1; i <= n; i++) { //前i栋房子,最后一栋房子为i //第i栋房子要染成j颜色
//这里计算的是将第i栋房子漆成颜色j的最小费用
for(int j = 0; j < 3; j++) { f[i][j] = 100000; //第i-1栋房子要染成K颜色 //这里的计算顺序是从前向后计算的 //在计算f[i][j]时,前面的元素都已经计算完全。 //所以这里f[i - 1][k]是已知量,是第i-1栋房子被染成颜色k的最小费用。用这个已知量来求f[i][j] //将这个循环套在j的循环之内,是因为求第i栋房子漆成颜色j时的费用,要求i-1的颜色k不能等于j // for(int k = 0; k < 3; k++) { if(j != k ) { f[i][j] = min(f[i][j], f[i - 1][k] + C[i - 1][j]); } } } } return min(f[n][0], f[n][1], f[n][2]); } }
序列型动态规划: ...前i个...最小/方式数/可行性
在设计动态规划过程中,发现需要知道油漆前N-1栋房子的最有策略中,房子N-2的颜色
如果只用f[N-1],将无法区分
解决方法:记录下房子N-2的颜色
- 在房子N-2是红/蓝/绿的情况下,油漆N-1栋房子的最小花费
序列 + 状态
划分型动态规划
题目:有一段由A-Z组成的字母串信息被加密成数字串
加密方式:A->1, B-> 2, ... , Z-> 26
给定加密后的数字串S[0 ... N-1], 问有所少种方式解密成字母串
例子:
输入:12 输出:2(AB或L)
组成部分一:确定状态
解密数字串,即划分成若干段数字,每段数字对应一个字母
最后一步:对应一个字母。(在划分型问题中,最后一步对应的是最后一段。无论怎么划分,最后一段数字一定对应一个字母)
-A, B, ... , Z
这个字母加密时对应的数字串为:1, 2, ... , 26
假设这是具有N个数字的数字串。

那么最后一个字母只能对应两个数字或者一个数字,除此之外没有其它的对应关系。
如果最后一个字母对应一位数字,那么在这个问题中就是2.那么字母就是B。假设前N-1个字母共有100种解密方式
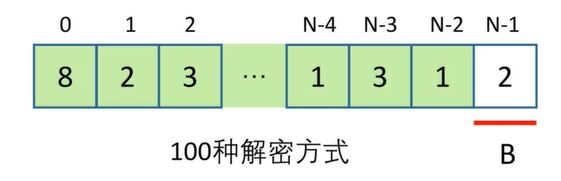
如果最后一个字母对应两位数字,那么在这个问题中就是数字12,对应的字母就是L。假设前N-2个字母共有50种解密方式
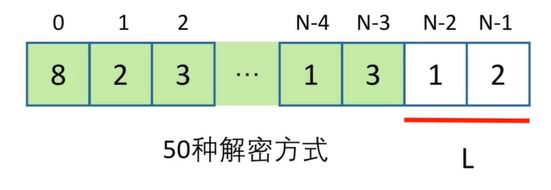
除此之外,最后一个字母没有其它的可能。那么

子问题
设数字串长度为N
原问题:要求数字串前N个字符的解密方式数
子问题:需要知道数字串前N-1和N-2个字符的解密方式数。
状态:设数字串前i个数字解密成字母串有f[i]种方式。
组成部分二:转移方程
设数字串S前i个数字揭密乘字母串有f[i]种方式,则

组成部分三:初始条件和边界情况
设数字串S前i个数字揭密乘字母串有f[i]种方式
初始条件:f[0] = 1, 即空串有1种方式解密 ,即解密成空串
边界情况:如果i = 1,只看最后一个数字
组成部分四:计算顺序
f[0], f[1], ... , f[N]