第三章、曲面的局部理论
1.曲面的概念
1.1.曲面的概念
1.2.切平面与法向

2.曲面的第一基本形式
![]()

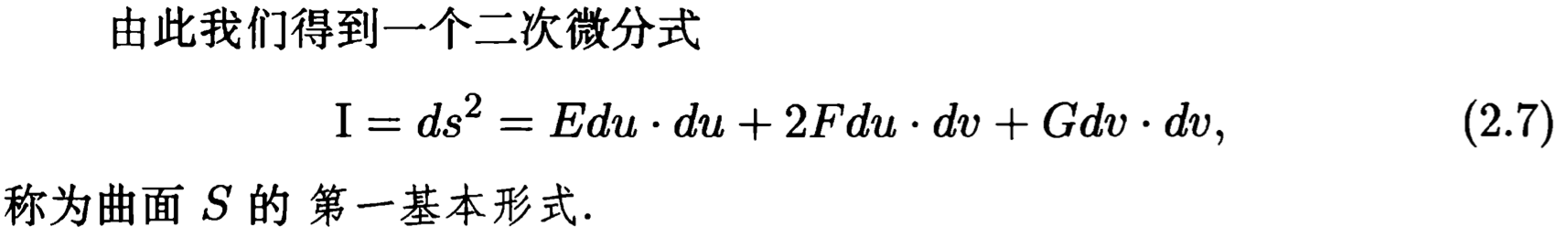
![]()


3.曲面的第二基本形式
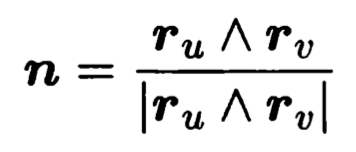
![]()
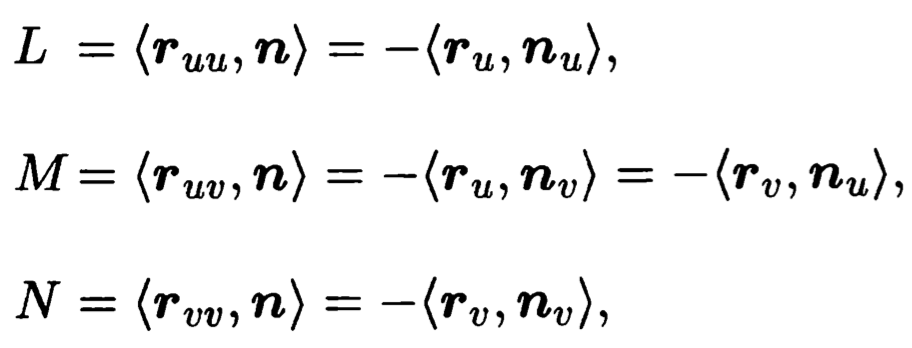
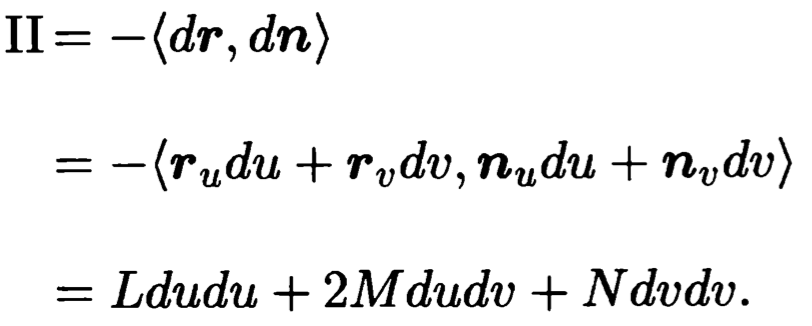

正定矩阵:一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z,都有zTMz> 0。其中zT表示z的转置。
正定矩阵在合同变换下可化为标准型, 即对角矩阵。
所有特征值大于零的对称矩阵(或厄米矩阵)也是正定矩阵。
判定定理1:对称阵A为正定的充分必要条件是:A的特征值全为正。
判定定理2:对称阵A为正定的充分必要条件是:A的各阶顺序主子式都为正。
判定定理3:任意阵A为正定的充分必要条件是:A合同于单位阵。
正定矩阵的性质:
1.正定矩阵的任一主子矩阵也是正定矩阵。
2.若A为n阶对称正定矩阵,则存在唯一的主对角线元素都是正数的下三角阵L,使得A=L*L′,此分解式称为 正定矩阵的乔列斯基(Cholesky)分解。
3.若A为n阶正定矩阵,则A为n阶可逆矩阵。
4.正定矩阵对角线元素都大于零。证明:取基向量,由定义可知其对角线元素均大于零。
负定矩阵:设A是实对称矩阵。如果对任意的实非零列矩阵X有XTAX<0,就称A为负定矩阵。
它在合同相似变换下,可以变成(-E), 这里 E 是单位矩阵。
1. A是负定矩阵的充要条件是:-A是正定矩阵。
2. A是负定矩阵的充要条件是:A^{-1}是负定矩阵。
3. A是负定矩阵的充要条件是:A的所有奇数阶顺序主子式小于零,所有偶数阶顺序主子式大于零。
4.负定矩阵对角线元素都小于零。证明:取基向量,由定义可知其对角线元素均小于零。
不定矩阵:若A∈Mn(K)是不定矩阵的充要条件是:存在列向量组X,Y,使得XTAX>0,YTAY<0。
若实对称矩阵A的主对角线上元素有正有负,则A一定是不定矩阵。


4.法曲率与Weingarten变换



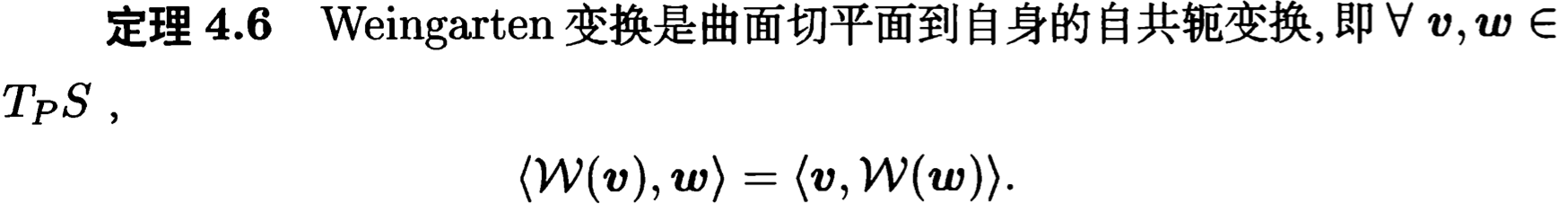
5.主曲率与Gauss曲率

![]()
6.曲面的一些例子
6.1.旋转曲面
6.1.1.常Gauss曲率旋转曲面
6.1.2.常平均曲率旋转曲面
6.2.直纹面与可展曲面

6.3.全脐点曲面
![]()