3.8____可持续化线段树(主席树)
3.8.1____权值线段树
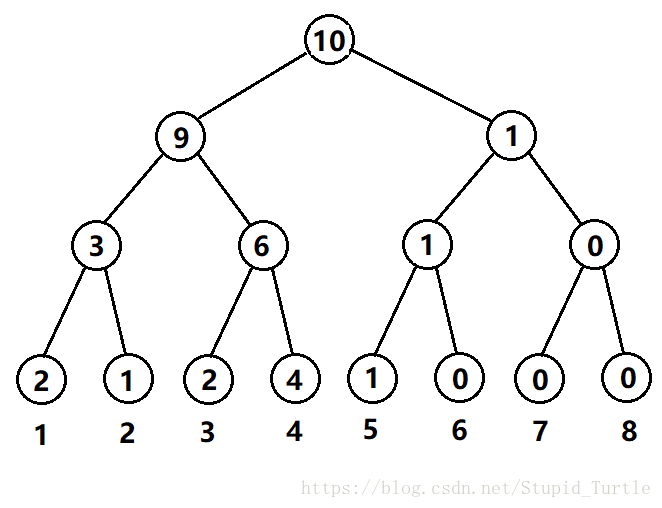
权值线段树之所以带上"权值"二字,是因为它是记录权值的线段树。所以在某些题中,需要离散化处理输出数据。记录权值指的是,每个点上存的是区间内的数字出现的总次数。比如一个长度为10的数组[1,1,2,3,3,4,4,4,4,5]。
1出现了两次所以节点[1,1]的权值为2
2出现了一次所以节点[2,2]的取值为1
因为1,2共出现三次所以节点[1,2]的权值为3
因为这个测试数据比较少,没有对数据进行离散化,所有会有权值为0的节点出现
应用求第K大(或小)数
我们向树中插入4个数 $ [1,2,5,7]$ ,得到的权值线段树如下
现在我们从根节点开始,向下去找第3(K)小的数(rt为当前节点的数组编号)
我们的判断准则为: 我们求的是区间 [1,7]的第3小数,首先我们要去看这个节点的左子树的取值为多少,如果K <= t[rt<<1].权值,那么我们的问题就缩小为了,找左儿子所在的区间内的第K小数;反之如果 K > t[rt<<1].权值,那么说明[1,7]的第K小数在他的右子树上,那么问题就变为了,找右儿子所在区间内的第K-t[rt<<1].权值小的数。
运用这个原理,第一层我们就把问题缩小为,求[5,7]区间第1小数,然后进第二层问题缩小为求[5,6]区间的第1小数,进入第三层我们就能找到我们的答案了,为5,这就是权值线段树求第K小(大)数的原理。
下面我们来看一道板子题
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
struct node
{
int l,r;
int cnt;
}t[N<<2];
int a[N];
void build(int rt,int l ,int r)
{
t[rt].l = l,t[rt].r = r;
if(l == r){
t[rt].cnt = 0;
return ;
}
int mid = l + r >>1;
build(rt <<1,l,mid),build(rt<<1|1,mid+1,r);
}
void update(int rt,int loc,int val)
{
if( t[rt].l == t[rt].r ){
t[rt].cnt += val;
return ;
}
int mid = t[rt].l + t[rt].r >> 1;
if( loc <= mid ) update(rt<<1,loc,val);
else update(rt<<1|1,loc,val);
t[rt].cnt = t[rt<<1].cnt + t[rt<<1|1].cnt;
}
int query(int rt,int k) ///query里的逻辑是关键点
{
if(t[rt].l == t[rt].r){
return t[rt].l;
}
int mid = t[rt].l + t[rt].r >> 1;
if( k <= t[rt<<1].cnt ) return query(rt<<1,k);
else return query(rt<<1|1,k - t[rt<<1].cnt);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,m;
cin >>n >> m;
build(1,1,1000002);
for(int i = 1; i <= n ; i++){
cin >> a[i];
update(1,a[i],1);
}
for(int i = 0; i < m ; i++){
int op,x,y;
cin >> op;
if(op == 1){
cin >>x;
cout << query(1,x) <<endl;
}
else{
cin >>x>> y;
if( a[x] == y ) continue;
update(1,a[x],-1);
update(1,y,1);
a[x] = y;
}
}
return 0;
}
3.8.2____主席树(可持续化线段树)
在知道了权值线段树是什么,那么我们就可以开始认识什么是主席树了。主席树是一棵可持久化线段树,可持久化指的是它保存了这棵树的所有历史版本。
最简单的办法是:如果你输入了n个数,那么每输入一个数字a[i],就构造一棵保存了从a[1]到a[i]的权值线段树。之所以这么做,是因为我们可以把第j棵树和第(i-1)棵树上的每个点的权值相减,来得到一颗新的权值线段树,而这个新的树相当于是除去a[i]之前的数,将第一个输入的数变为a[i+1],最后一个输入的数为a[i]的权值线段树了,那么求区间K小值,就变成上面权值线段树的内容了。
如果这么说不太好理解的话,我们可以思考另外一个模型:求数组a[1]到a[n]的和。如果只是求[1,n]这一段的和,那么我们直接全部加起来就可以了,或者求一个前缀和sum[n]即可。那么如果我给定了l和r,想要知道[l,r]这段区间上的和呢?是不是利用前缀和sum[r]-sum[l-1]就可以轻松得到?那么主席树的思想也是如此,将tree[r]-tree[l-1]得到的一棵权值线段树即为属于[l,r]的一棵权值线段树,那么在这么一棵权值线段树上求第k大不是就转变为之前的问题了么。

还有一个问题需要解决,那就是空间问题。
显而易见的是,如果每输入一个数就重新构造一棵权值线段树,必然会导致空间不够用:一棵线段树的空间就是n * 4,那么一共的空间开销就是n * n * 4,显然是会MLE的。那么这个问题怎么解决呢?
可以发现每更新一个点,就会从它开始把它的所有祖先都更新一次,而其他的点都没有被改变,即:每次改变的结点只有(log_n)个。这样,我们每次输入一个数,只需要多开logn个空间,那么实际的空间开销只有(n*(4+log_n)),满足了空间要求。
#include <bits/stdc++.h>
using namespace std;
const int N =100005;
/// len为离散化之后数组的长度,a为原始数组,d为离散化之后的数组
int n,m,len,a[N],d[N];
/// T为[1,i]区间的权值线段树的根节点下标,idx为当前存到那个下标了
int T[N],idx;
struct node
{
int l,r,val;
/// 主席树的l,r与线段树不同,l存的是左儿子的节点下标,r存的是...
}t[4*N + N*17];
int build(int l,int r)
{
int p = ++idx , mid = l + r >> 1;
if(l < r){
t[p].l = build(l,mid);
t[p].r = build(mid+1,r);
}
t[p].val = 0;
return p;
}
/// 添加一个数,pre为上颗树的根节点,T[0]为build的空树,T[1]为加入一个节点时的树
/// 每次都只添加一条路径(其余的连上上一颗树的节点),因为一次只增加一个点
int update(int pre,int l ,int r,int val)
{
int p = ++idx,mid = l + r >>1;
/// 链接上颗树
t[p].l = t[pre].l , t[p].r = t[pre].r , t[p].val = t[pre].val + 1;
if(l < r){ /// 只更新修改的那条路径,并新建点
if( val <= mid ) t[p].l = update(t[pre].l , l ,mid ,val);
else t[p].r = update(t[pre].r,mid+1,r,val);
}
return p;
}
int query(int x,int y,int l,int r,int k)
{
if(l == r) return l; ///权值线段树的特点
/// 对位相减,得到[l,r]区间的权值线段树的对应节点值
int sum = t[ t[y].l ].val - t[ t[x].l ].val, mid = l + r >> 1;
/// 下面的和权值线段树相同
if( k <= sum ) return query( t[x].l,t[y].l,l,mid,k );
else return query( t[x].r,t[y].r,mid + 1,r ,k - sum );
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n ; i++){
cin >> a[i];
d[i] = a[i];
}
sort(d+1,d+n+1);
len = unique(d+1,d+1+n) - (d+1); ///地址相减
for(int i = 1; i <= n ; i++){
a[i] = lower_bound(d+1,d+1+len,a[i]) - d; ///离散化映射
}
///建树
T[0] = build(1,len);
for(int i = 1; i <= n ; i++) T[i] = update(T[i-1],1,len,a[i]);
while(m--){
int l,r,k;
cin >> l >> r >>k;
int ans = query(T[l-1],T[r],1,len,k);
cout << d[ans] <<endl;
}
return 0;
}