一阶线性微分方程求特解(附图).
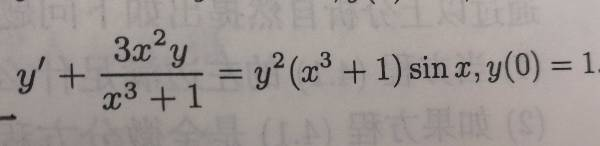
^let
u= (x^3+1)y
du/dx = (x^3+1) dy/dx + 3x^2. y
//
y' +3x^2.y/(x^3+1) = y^2.(x^3+1). sinx
(x^3+1)y' +3x^2.y = y^2.(x^3+1)^2. sinx
du/dx = u^2 .sinx
∫ du/u^2 = ∫ sinx dx
1/u = cosx +C
1/[(x^3+1)y] = cosx +C
y(0) =1
1= 1 +C
=> C=0
1/[(x^3+1)y] = cosx
y= 1/[cosx .(x^3+1)]

微分方程的特解怎么求
一般式是这样的ay''+by'+cy=f(x)
第一步:求特征根
令ar²+br+c=0,解得r1和r2两个值,(这里可以是复数,例如(βi)²=-β²)
第二步:通解
1、若r1≠r2,则y=C1*e^(r1*x)+C2*e^(r2*x)
2、若r1=r2,则y=(C1+C2x)*e^(r1*x)
3、若r1,2=α±βi,则y=e^(αx)*(C1cosβx+C2sinβx)
第三步:特解
f(x)的形式是e^(λx)*P(x)型,(注:P(x)是关于x的多项式,且λ经常为0)
则y*=x^k*Q(x)*e^(λx) (注:Q(x)是和P(x)同样形式的多项式,例如P(x)是x²+2x,则设Q(x)为ax²+bx+c,abc都是待定系数)
1、若λ不是特征根 k=0 y*=Q(x)*e^(λx)
2、若λ是单根 k=1 y*=x*Q(x)*e^(λx)
3、若λ是二重根 k=2 y*=x²*Q(x)*e^(λx)(注:二重根就是上面解出r1=r2=λ)
f(x)的形式是e^(λx)*P(x)cosβx或e^(λx)*P(x)sinβx
1、若α+βi不是特征根,y*=e^λx*Q(x)(Acosβx+Bsinβx)
2、若α+βi是特征根,y*=e^λx*x*Q(x)(Acosβx+Bsinβx)(注:AB都是待定系数)
第四步:解特解系数
把特解的y*'',y*',y*都解出来带回原方程,对照系数解出待定系数。
最后结果就是y=通解+特解。
通解的系数C1,C2是任意常数。
拓展资料:
微分方程
微分方程指描述未知函数的导数与自变量之间的关系的方程。微分方程的解是一个符合方程的函数。而在初等数学的代数方程,其解是常数值。
高数常用微分表
唯一性
存在定一微 分程及约束条件,判断其解是否存在。唯一性是指在上述条件下,是否只存在一个解。针对常微分方程的初值问题,皮亚诺存在性定理可判别解的存在性,柯西-利普希茨定理则可以判别解的存在性及唯一性。针对偏微分方程,柯西-克瓦列夫斯基定理可以判别解的存在性及唯一性。 皮亚诺存在性定理可以判断常微分方程初值问题的解是否存在。
