可直接等价替换的类型: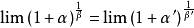
变上限积分函数(积分变限函数)也可以用等价无穷小进行替换。

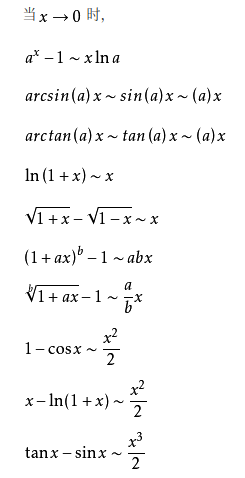

泰勒展开式的重要性体现在以下五个方面:
1、幂级数的求导和积分可以逐项进行,因此求和函数相对比较容易。
2、一个解析函数可
3、泰勒级数可以用来近似计算函数的值,并估计误差。
4、证明不等式。
5、求待定式的极限。
常用泰勒展开公式如下:
1、e^x = 1+x+x^2/2!+x^3/3!+……+x^n/n!+……
2、ln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|<1)
3、sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。(-∞<x<∞)
4、cos x = 1-x^2/2!+x^4/4!-……+(-1)k*(x^(2k))/(2k)!+…… (-∞<x<∞)
5、arcsin x = x + 1/2*x^3/3 + 1*3/(2*4)*x^5/5 + ……(|x|<1)
6、arccos x = π - ( x + 1/2*x^3/3 + 1*3/(2*4)*x^5/5 + …… ) (|x|<1)
7、sinh x = x+x^3/3!+x^5/5!+……+(-1)^(k-1)*(x^2k-1)/(2k-1)!+…… (-∞<x<∞)




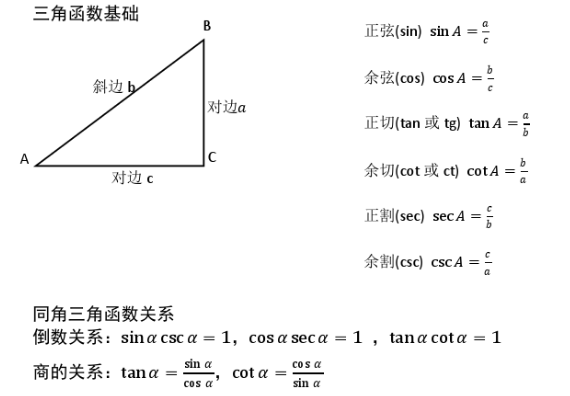
总结:人类的本质是复读机,多看多学。