区块链中的密码学之默克尔树(十五)

目录

1. 前言

2. 默克尔树

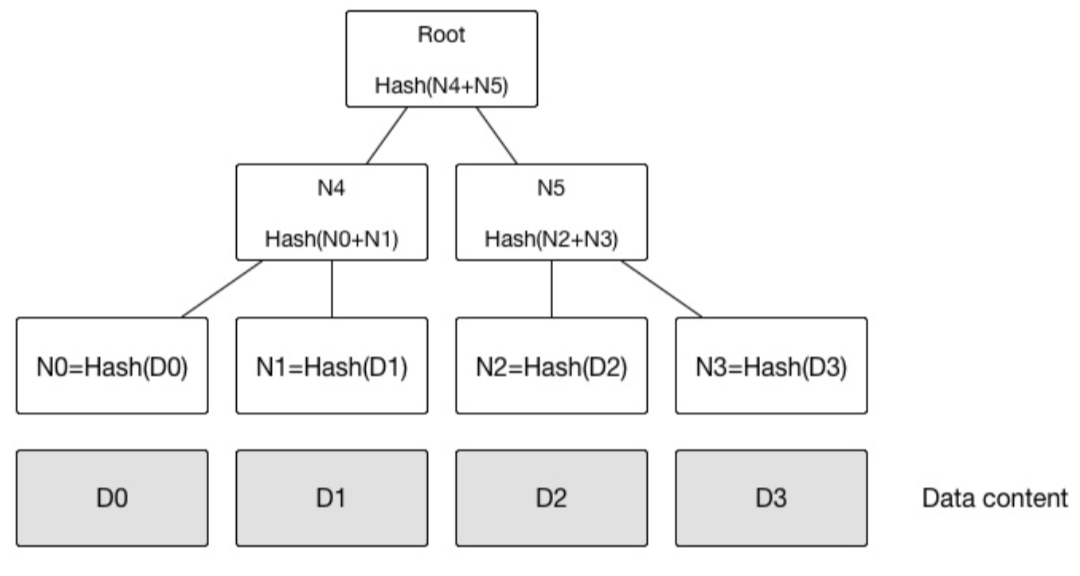
默克尔树（ 又叫哈希树） 是一种二叉树，由一个根节点、一组中间节点和一组叶节点组成。最下面的叶节点包含存储数据或其哈希值，每个中间节点是它的两个孩子节点内容的哈希值，根节点也是由它的两个子节点内容的哈希值组成。

进一步的，默克尔树可以推广到多叉树的情形。
默克尔树的特点是，底层数据的任何变动，都会传递到其父亲节点，一直到树根。
默克尔树的典型应用场景包括：

  • 快速比较大量数据：当两个默克尔树根相同时，则意味着所代表的数据必然相同。
  • 快速定位修改：例如上例中，如果 D1 中数据被修改，会影响到 N1，N4 和 Root。因此，沿着 Root --> N4 --> N1，可以快速定位到发生改变的 D1；时间复杂度为O(logn)
  • 零知识证明：例如如何证明某个数据（ D0……D3） 中包括给定内容 D0，很简单，构造一个默克尔树，公布 N0，N1，N4，Root，D0 拥有者可以很容易检测 D0 存在，但不知道其它内容。

默克尔树的查找的时间复杂度为O（logn）。对于Merkle Tree数据块的更新操作其实是很简单的，更新完数据块，然后接着更新其到树根路径上的Hash值就可以了，这样不会改变Merkle Tree的结构。

3. 布隆过滤器

布隆过滤器是一种基于Hash的高效查找结构，能够快速（常数时间内）回答“某个元素是否在一个集合内”的问题。

其本质上是利用了hash算法的查找的时间复杂度为O(1)，但其缺点是空间复杂度过高，空间利用率太低，一般不会超过50%，Bloom Filter进行了折中，即使用了多个hash函数，大大降低了空间复杂度，于此同时，时间复杂度也基本不变。但其也是有代价的，其不是精确匹配的，于此相比，hash表则是精确匹配的，所以任何事情都是有代价的。

什么情况下需要布隆过滤器？

先来看几个比较常见的例子

  • 字处理软件中，需要检查一个英语单词是否拼写正确
  • 在 FBI，一个嫌疑人的名字是否已经在嫌疑名单上
  • 在网络爬虫里，一个网址是否被访问过
  • yahoo, gmail等邮箱垃圾邮件过滤功能

这几个例子有一个共同的特点： 如何判断一个元素是否存在一个集合中？

常规思路

  • 数组
  • 链表
  • 树、平衡二叉树、Trie
  • Map (红黑树)
  • 哈希表

虽然上面描述的这几种数据结构配合常见的排序、二分搜索可以快速高效的处理绝大部分判断元素是否存在集合中的需求。但是当集合里面的元素数量足够大，如果有500万条记录甚至1亿条记录呢？这个时候常规的数据结构的问题就凸显出来了。数组、链表、树等数据结构会存储元素的内容，一旦数据量过大，消耗的内存也会呈现线性增长，最终达到瓶颈。有的同学可能会问，哈希表不是效率很高吗？查询效率可以达到O(1)。但是哈希表需要消耗的内存依然很高。使用哈希表存储一亿 个垃圾 email 地址的消耗？哈希表的做法：首先，哈希函数将一个email地址映射成8字节信息指纹；考虑到哈希表存储效率通常小于50%（哈希冲突）；因此消耗的内存：8 * 2 * 1亿 字节 = 1.6G 内存，普通计算机是无法提供如此大的内存。这个时候，布隆过滤器（Bloom Filter）就应运而生。

布隆过滤器介绍

巴顿.布隆于一九七零年提出，一个很长的二进制向量 （位数组），一系列随机函数 (哈希)，空间效率和查询效率高，有一定的误判率（哈希表是精确匹配）。

布隆过滤器原理

布隆过滤器（Bloom Filter）的核心实现是一个超大的位数组和几个哈希函数。假设位数组的长度为m，哈希函数的个数为k

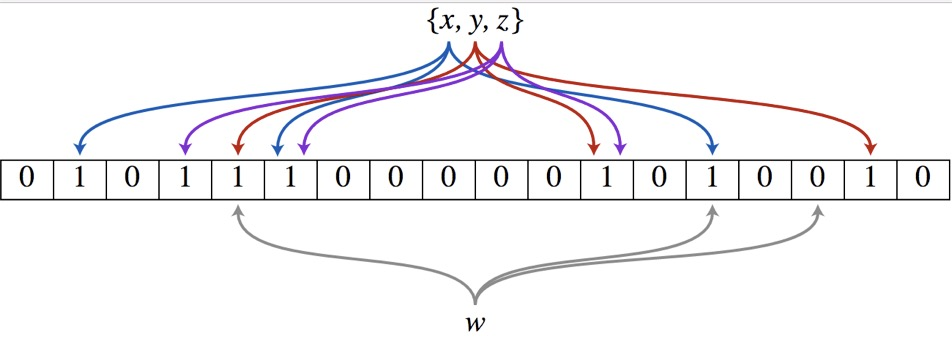
以上图为例，具体的操作流程：假设集合里面有3个元素{x, y, z}，哈希函数的个数为3。首先将位数组进行初始化，将里面每个位都设置位0。对于集合里面的每一个元素，将元素依次通过3个哈希函数进行映射，每次映射都会产生一个哈希值，这个值对应位数组上面的一个点，然后将位数组对应的位置标记为1。查询W元素是否存在集合中的时候，同样的方法将W通过哈希映射到位数组上的3个点。如果3个点的其中有一个点不为1，则可以判断该元素一定不存在集合中。反之，如果3个点都为1，则该元素可能存在集合中。注意：此处不能判断该元素是否一定存在集合中，可能存在一定的误判率。可以从图中可以看到：假设某个元素通过映射对应下标为4，5，6这3个点。虽然这3个点都为1，但是很明显这3个点是不同元素经过哈希得到的位置，因此这种情况说明元素虽然不在集合中，也可能对应的都是1，这是误判率存在的原因。

布隆过滤器添加元素

  • 将要添加的元素给k个哈希函数
  • 得到对应于位数组上的k个位置
  • 将这k个位置设为1

布隆过滤器查询元素

  • 将要查询的元素给k个哈希函数
  • 得到对应于位数组上的k个位置
  • 如果k个位置有一个为0，则肯定不在集合中
  • 如果k个位置全部为1，则可能在集合中

4. 同态加密

链接：https://www.zhihu.com/question/27645858/answer/37598506

4.1 概览：同态加密的概念

同态加密（Homomorphic Encryption）是很久以前密码学界就提出来的一个Open Problem。早在1978年，Ron Rivest, Leonard Adleman, 以及Michael L. Dertouzos就以银行为应用背景提出了这个概念[RAD78]。对，你没有看错，Ron Rivest和Leonard Adleman分别就是著名的RSA算法中的R和A。至于中间的S，Adi Shamir，现在仍然在为密码学贡献新的工作。

什么是同态加密？

提出第一个构造出全同态加密（Fully Homomorphic Encryption）[Gen09]的Craig Gentry给出的直观定义最好：

A way to delegate processing of your data, without giving away access to it.

这是什么意思呢？一般的加密方案关注的都是数据存储安全。即，我要给其他人发个加密的东西，或者要在计算机或者其他服务器上存一个东西，我要对数据进行加密后在发送或者存储。没有密钥的用户，不可能从加密结果中得到有关原始数据的任何信息。只有拥有密钥的用户才能够正确解密，得到原始的内容。我们注意到，这个过程中用户是不能对加密结果做任何操作的，只能进行存储、传输。对加密结果做任何操作，都将会导致错误的解密，甚至解密失败。

同态加密方案最有趣的地方在于，其关注的是数据处理安全。同态加密提供了一种对加密数据进行处理的功能。也就是说，其他人可以对加密数据进行处理，但是处理过程不会泄露任何原始内容。同时，拥有密钥的用户对处理过的数据进行解密后，得到的正好是处理后的结果。

有点抽象？我们举个实际生活中的例子。有个叫Alice的用户买到了一大块金子，她想让工人把这块金子打造成一个项链。但是工人在打造的过程中有可能会偷金子啊，毕竟就是一克金子也值很多钱的说… 因此能不能有一种方法，让工人可以对金块进行加工（delegate processing of your data），但是不能得到任何金子（without giving away access to it）？当然有办法啦，Alice可以这么做：

  • Alice将金子锁在一个密闭的盒子里面，这个盒子安装了一个手套。
  • 工人可以带着这个手套，对盒子内部的金子进行处理。但是盒子是锁着的，所以工人不仅拿不到金块，连处理过程中掉下的任何金子都拿不到。
  • 加工完成后。Alice拿回这个盒子，把锁打开，就得到了金子。

这个盒子的样子大概是这样的：

这里面的对应关系是：

  • 盒子：加密算法
  • 盒子上的锁：用户密钥
  • 将金块放在盒子里面并且用锁锁上：将数据用同态加密方案进行加密
  • 加工：应用同态特性，在无法取得数据的条件下直接对加密结果进行处理
  • 开锁：对结果进行解密，直接得到处理后的结果

同态加密哪里能用？

这几年不是提了个云计算的概念嘛。同态加密几乎就是为云计算而量身打造的！我们考虑下面的情景：一个用户想要处理一个数据，但是他的计算机计算能力较弱。这个用户可以使用云计算的概念，让云来帮助他进行处理而得到结果。但是如果直接将数据交给云，无法保证安全性啊！于是，他可以使用同态加密，然后让云来对加密数据进行直接处理，并将处理结果返回给他。这样一来：

  • 用户向云服务商付款，得到了处理的结果；
  • 云服务商挣到了费用，并在不知道用户数据的前提下正确处理了数据；

这方法简直完美啊有没有？！但是，这么好的特性肯定会带来一些缺点。同态加密现在最需要解决的问题在于：效率。效率一词包含两个方面，一个是加密数据的处理速度，一个是这个加密方案的数据存储量。我们可以直观地想一想这个问题：

  • 工人戴着手套加工金子，肯定没有直接加工来得快嘛~ 也就是说，隔着手套处理，精准度会变差（现有构造会有误差传递问题），加工的时间也会变得更长（密文的操作花费更长的时间），工人需要隔着操作，因此也需要更专业（会正确调用算法）。
  • 金子放在盒子里面，为了操作，总得做一个稍微大一点的盒子吧，要不然手操作不开啊（存储空间问题）。里面也要放各种工具吧，什么电钻啦，锉刀啦，也需要空间吧？

这种加密方案真的有在研究？

我举3个简单的例子：

  1. 第一个构造出全同态加密方案的人是Gentry，这是他在Stanford攻读博士学位的研究成果。Gentry毕业后去哪里了呢？IBM。大家知道IBM可是一个云服务提供商啊！在IBM，Gentry和另一个密码学大牛Halevi继续进行同态加密及其相关的研究，并实现了一些同态加密方案。如果IBM真的做出了可以在实际使用的同态加密方案，那么其他云服务提供商就可以拜拜了啊！这游戏不用玩了啊，人家能在不知道数据内容得前提下处理数据啊，毕竟谁都不想把数据泄露给其他公司啊！
  2. 国内的某个大公司（具体是哪个我就不透露了…）对这方面的研究非常感兴趣，我也和他们做了一次交流，并且初步达成了一定的研究大方向。要不怎么我现在也去弄这个头大的东西呢。要知道，国内的公司也没闲着，这是制高点，拿到了就是一家独大，而且是超级技术垄断，不公开源代码或者不了解内部构造的话想仿造都仿造不了啊…不过，这方面的研究说实话Gap确实大，入门起码要3个月的时间，还不一定做的出来…
  3. 即使没有实现全同态加密，也可以得到其他一些很有趣的结论。而每一个结论都可能引发技术垄断。这些结论由于涉及到了一定的基础知识，我在后面中会进行介绍。

业界如何评价全同态加密的构造？

在此引用一个前辈的话：

如果未来真的做出了Practical Fully Homomorphic Encryption，那么Gentry一定可以得到图灵奖。

剩下的，我也就不用多说了吧…

4.2 同态加密的定义、安全性和简单实例

下面的内容，如果可以接受符号表述，具有一点密码学的知识，对抽象代数有一定的了解的话，可能体会的更深刻哦。

同态加密具体如何定义？

我们在云计算应用场景下面进行介绍：

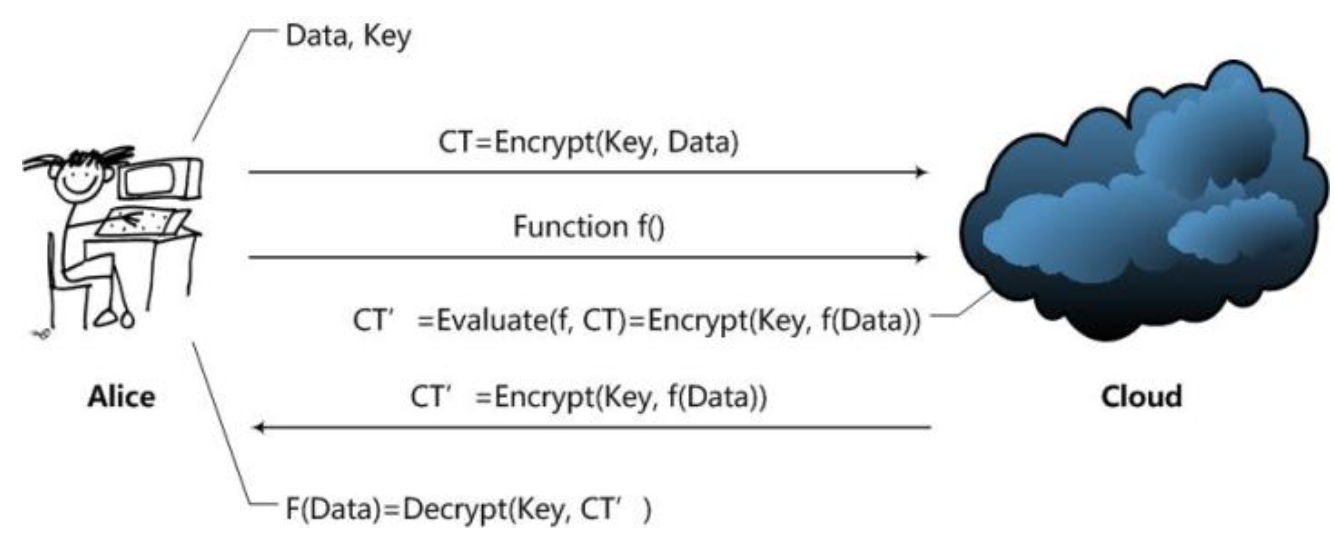
Alice通过Cloud，以Homomorphic Encryption（以下简称HE）处理数据的整个处理过程大致是这样的：

  1. Alice对数据进行加密。并把加密后的数据发送给Cloud；
  2. Alice向Cloud提交数据的处理方法，这里用函数f来表示；
  3. Cloud在函数f下对数据进行处理，并且将处理后的结果发送给Alice；
  4. Alice对数据进行解密，得到结果。

据此，我们可以很直观的得到一个HE方案应该拥有的函数：

  1. KeyGen函数：密钥生成函数。这个函数应该由Alice运行，用于产生加密数据Data所用的密钥Key。当然了，应该还有一些公开常数PP（Public Parameter）；
  2. Encrypt函数：加密函数。这个函数也应该由Alice运行，用Key对用户数据Data进行加密，得到密文CT（Ciphertext）；
  3. Evaluate函数：评估函数。这个函数由Cloud运行，在用户给定的数据处理方法f下，对密文进行操作，使得结果相当于用户用密钥Key对f(Data)进行加密。
  4. Decrypt函数：解密函数。这个函数由Alice运行，用于得到Cloud处理的结果f(Data)。

那么，f应该是什么样子的呢？HE方案是支持任意的数据处理方法f？还是说只支持满足一定条件的f呢？根据f的限制条件不同，HE方案实际上分为了两类：

  • Fully Homomorphic Encryption (FHE)：这意味着HE方案支持任意给定的f函数，只要这个f函数可以通过算法描述，用计算机实现。显然，FHE方案是一个非常棒的方案，但是计算开销极大，暂时还无法在实际中使用。
  • Somewhat Homomorphic Encryption (SWHE)：这意味着HE方案只支持一些特定的f函数。SWHE方案稍弱，但也意味着开销会变得较小，容易实现，现在已经可以在实际中使用。

什么叫做安全的HE？
HE方案的最基本安全性是语义安全性（Semantic Security）。直观地说，就是密文（Ciphertext）不泄露明文（Plaintext）中的任意信息。这里密文的意思就是加密后的结果；明文的意思就是原始的数据。如果用公式表述的话，为：
forall m_0, m_1, extbf{Encrypt}(PK, m_0) approx extbf{Encrypt}(PK, m_1)
这里PK代表公钥（Public Key），是非对称加密体制中可以公开的一个量。公式中的"约等于"符号，意味着多项式不可区分性，即不存在高效的算法，可以区分两个结果，即使已知m0, m1和PK。有人说了，这怎么可能？我已经知道m0, m1了，我看到加密结果后，对m0或者m1在执行一次加密算法，然后看哪个结果和给定结果相同不就完了？注意了，加密算法中还用到一个很重要的量：随机数。也就是说，对于同样的明文m进行加密，得到的结果都不一样，即一个明文可以对应多个密文（many ciphertexts per plaintext）。

在密码学中，还有更强的安全性定义，叫做选择密文安全性（Chosen Ciphertext Security）。选择密文安全性分为非适应性（None-Adaptively）和适应性（Adaptively），也就是CCA1和CCA2，HE方案是不可能做到CCA2安全的。那么，HE方案能不能做到CCA1安全呢？至今还没有CCA1安全的FHE方案，但是在2010年，密码学家们就已经构造出了CCA1的SWHE方案了[LMSV10]。

HE方案还有一方面的安全性，就是函数f是不是也可以保密呢？这样的话HE就更厉害了！Cloud不仅不能够得到数据本身的内容，现在连数据怎么处理的都不知道，只能按照给定的算法执行，然后返回的结果就是用户想要的结果。如果HE方案满足这样的条件，我们称这个HE方案具有Function-Privacy特性。不过，仅我个人所了解到的，现在还没有Function-privacy FHE，甚至Function-privacy SWHE也没有。

不过，Function-privacy引入了另一个很有趣的概念，那就是我们能不能反过来，就做到Function-privacy，但是不用做到数据隐私呢？这其实也有很好的应用场景：比如一个天才设计了一个算法（想象Jeffrey Dean设计了历史上第一个O(1/n)复杂度算法，或者设计了一个O(n^2)算法，但是是用来解决旅行商问题的），但是他不想把这个算法公开。他只提供一个程序，这个程序不泄露任何算法本身的内容，人们只能调用这个算法，然后得到输出的结果。这个特别像什么？对啦，就是程序的编译与反编译嘛。如果Function-privacy的加密设计出来了，那么计算机科学家们就可以一劳永逸地阻止程序反编译，甚至连破解都杜绝了。满足这样条件的加密方案，即，给算法加密的方案，叫做Obfuscation。很遗憾，2001年，密码学家们已经证明，不可能实现严格意义上的Obfuscation [BGIRSVY01]。但是，可以做到一个称为Indistinguishability Obfuscation的东西。这个东西是密码学家们研究同态加密过程中的一个产物，现在已经有了一些候选方案了[GGHRSB13]。这个就不展开说了，是另一个领域的内容。

举个SWHE的例子？
在2009年Graig Gentry给出FHE的构造前，很多加密方案都具有Somewhat Homomorphism的性质。实际上，最最经典的RSA加密，其本身对于乘法运算就具有同态性。Elgamal加密方案同样对乘法具有同态性。Paillier在1999年提出的加密方案也具有同态性，而且是可证明安全的加密方案哦！后面还有很多啦，比如Boneh-Goh-Nissim方案[BGN05], Ishai-Paskin方案等等。不过呢，2009年前的HE方案要不只具有加同态性，要不只具有乘同态性，但是不能同时具有加同态和乘同态。这种同态性用处就不大了，只能作为一个性质，这类方案的同态性一般也不会在实际中使用的。

在此我们看一下Elgamal加密方案，看看怎么个具有乘同态特性。Elgamal加密方案的密文形式为：
CT=(C_1, C_2)=(gr,hr cdot m)
其中r是加密过程中选的一个随机数，g是一个生成元，h是公钥。如果我们有两个密文：
CT_1 = (g{r_1},h{r_1} cdot m_1), CT_2 = (g{r_2},h{r_2} cdot m_2)
我们把这两个密文的第一部分相乘，第二部分相乘，会得到：
CT= (g^{r_1} cdot g{r_2},h{r_1} cdot m_1 cdot h^{r_2} cdot m_2)=(g^{r_1 + r_2}, h^{r_1 + r_2} cdot m_1m_2)
也就是说，相乘以后的密文正好是m1m2所对应的密文。这样，用户解密后得到的就是m1m2的结果了。而且注意，整个运算过程只涉及到密文和公钥，运算过程不需要知道m1m2的确切值。所以我们说Elgamal具有乘同态性质。但是很遗憾，其没有加同态性质。

HE的效率如何？
2011年，Gentry和Halevi在IBM尝试实现了两个HE方案：Smart-Vercauteren的SWHE方案[SV10]以及Gentry的FHE方案[Gen09]，并公布了效率。结果如何呢？我们给出Gentry公布的数据（原始数据可以在2nd Bar-Ilan Winter School on Cryptography找到）Smart-Vercauteren的SWHE方案效率如下：

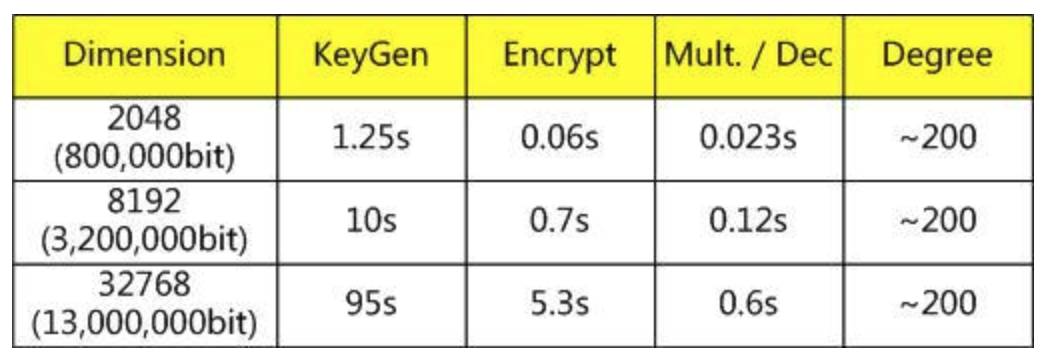
看着好像还行，不过这Dimension有点夸张啊…也就是说公钥很长…那么，Gentry的FHE方案如何呢？效率如下：

image-20190406102743856

公钥2.3GB，KeyGen需要2个小时，也是醉了…

==============================

三、 现有HE方案的安全假设和构造概览

如果你致力于HE的研究，我们给出一些可用的资料。

如何证明HE方案的安全性？
对于现在的密码学方案，安全性证明要把它规约到解决一个公开的困难问题上。简单地说，就是如果方案被破解了，那么攻击者可以用破解算法解决一个困难问题。然而，由于这个困难问题还没有找到高效的（多项式复杂度的）算法，因此方案是安全的。

那么，2009年以后的HE方案是建立在哪个困难问题上呢？是一个被称作Learning With Errors（LWE）的困难问题[Reg05]。后来，随着另一个新的工具出现，密码学家们又致力于基于Ring Learning With Errors（Ring-LWE）问题的HE构造[LPR10]。

Ring-LWE涉及到抽象代数中Ring以及Ideal的概念，稍显复杂。我们这里简单介绍一下LWE问题，Ring-LWE问题和它有点像。LWE问题分为两类，一个叫做Search-LWE，一个叫做Decision-LWE。Search-LWE可以简单地用下图来表示，其中A是一个m*n的矩阵，由Zp中的元素组成；s是一个n维向量；e是一个m维向量；b是一个m维向量：

image-20190406102804594

这个问题大致为：选择一个秘密（secret）值s，并选择一个范数很小的扰乱（error）向量e，计算b = As + e mod q。这个问题是：只给定矩阵A和计算的结果b（图中红色部分），不给定s和e（途中蓝色部分），反过来求秘密值s的大小。Decision-LWE问题有点类似：给定A和b，算法需要判断，b是由某个s通过As + e计算得来的呢，还是就是一个随机量呢？这里有几个小问题：

  1. m和n有多大？这取决于我们要求安全度有多高了。实际上这还取决于一些其他因素。
  2. e的范数要多么小？LWE要求e的取值要满足离散高斯分布（Discrete Gaussian Distribution）。
  3. 怎么想到的这么个问题？实际上，LWE问题是Lattice中的一个问题。Lattice是什么呢？这个展开说就有点累了…

如果知乎er们想了解更多有关Abstract Algebra，Lattice，以及LWE的内容，下面的三个材料是可以阅读的：

  • Harvard Extension School的Abstract Algebra课程。这门课可以帮助快速入门Abstract Algebra。当然了，这可是Harvard学生的本科课程哦。Abstract Algebra

  • 2nd Bar-Ilan Winter School on Cryptography。Bar-llan大学自2011年开始每年都组织一次密码学的Winter School，请的都是大牛啊！2012年的主题是Lattice-Based Cryptography，2013年的主题是Pairing-Based Cryptography。2015年2月，新的一轮Winter School就开始了，知乎上

    @刘健

    同学要去听的哦，羡慕嫉妒恨呢！

    2nd Bar-Ilan Winter School on Cryptography

  • Oded Regev的Lecture Notes on Lattice。Regev是谁？是他提出的LWE和Ring-LWE，所以他课程的材料当然有价值一听。Lattices in Computer Science (Fall 2009)

介绍一下构造FHE的思路？

FHE最重要的一点是Fully，就是说要支持任意的函数f。因此我们也可以很明显看出，想要构造FHE，就需要了解计算机是如何计算的。一般来说，我们有两种思路：

  • 从计算机原理考虑。计算机无论做何种运算，归根到底都是位运算。那么，计算机至少要支持哪些位运算，才能够支持所有的运算呢？实际上，一个计算机只要支持逻辑与运算（AND），以及异或运算（XOR），那么这个计算机理论上就可以实现计算机的其他运算了（我们称之为图灵完备性，Turing Completeness）
  • 从抽象代数考虑。我们只需要加法和乘法就可以完成全部运算了。但其实更严格的说，只要我们在一个域（Field）上构造HE，理论上我们就可以支持所有的f。

基于LWE问题的FHE只能针对1 bit进行加密，因此现在的构造都是从计算机原理考虑。也就是在bit的层面上实现FHE方案，或者更严谨地说，从电路层（Circuit）实现FHE方案。具体构造呢，大家刻意参考下面给出的参考文献了。实话实说，我自己也没有都消化，或者更严格地说，Regev的LWE构造论文我还没有完全看明白。

5. 零知识证明

零知识证明（ Zero-knowledge proofs）

链接：https://zhuanlan.zhihu.com/p/50121048

参考链接

零知识证明的提出

1985年 goid wasser, micali, rackoff 首次提出交互式零知识证明，发表了一篇名为《the knowledge complexity of interactive proof》的论文，他们的论文中首次提出了一个交互式证明系统，利用了图灵机的计算模型，这个模型的特点是会预设一些接收或者拒绝的状态，如果进入这些状态，则停机，如果不能进入任何接收或者拒绝的状态，则永不停机。也就是说，如果我们能输入正确的信息，进入到图灵机预设的状态，那么图灵机则会停机。

交互式证明系统定义：

定义 L subseteq{{0,1}^*}这样的一个正则语言，(P,V) 是图灵机的一个交互对，V是一个多项式时间的，当满足以下两个条件时，则称(P,V) 是关于L的一个交互式证明系统。

  • 对 forall x in L ,作为 (P,V) 的输入，V接受并且停止的概率至少为 1-frac {1}{n^k} .
  • 对任意的图灵机 P' , forall x otin L ,作为(P',V) 的输入，V接受的最大概率是 frac{1}{n^k} .

其中，k表示次数，n表示输入的长度。

什么意思呢，可以这样理解，P和V在完成交互作用过程后，如果 xin L ,那么V在高概率的条件下相信这是事实，这一条成为完备性（completeness）,但如果 x otin L ，那么在高概率条件下P不可能欺骗V，使V相信 x in L ,这一条成为公正性（soundness）,有的也称为正确性。这里提到的完备性和公正性就是零知识证明的性质的其中两条，还有一条是零知识性（后面会再提到）。

为了使大家更好地理解这个概念，我们举一个例子。

如图，洞穴里有一个秘密，知道咒语的人能打开C和D之间的密门。对其他任何人来说，两条通道都是死胡同。Peggy知道这个洞穴的秘密。她想对Victor证明这一点，但是她不想透露咒语。下面是她如何使Victor相信的过程：

  1. Victor 站在A点。

  2. Peggy一直走进洞穴，到达C点或者D点。

  3. 在Peggy消失在洞穴中之后，Victor走到B点。

  4. Victor向Peggy喊叫，要她：
    从左通道出来，或者 从右通道出来。

  5. Peggy答应了，如果有必要她就用咒语打开密门。

  6. Peggy和Victor 重复第1~5步n次。

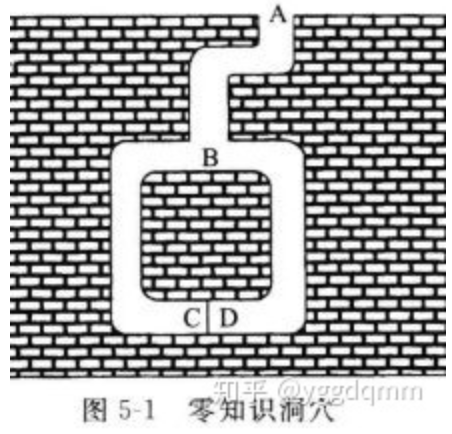
假设这个过程重复了十次，我们把这个例子放到刚才提到的交互式系统中，在Peggy知道咒语的情况下，那么她有很高的概率（ 1-frac{1}{2^{10}} ）让Victor相信她知道这个咒语（完备性），但是如果她不知道咒语，那么Victor相信的概率最大为 frac{1}{2^{10}} ,也就是有很高的概率Peggy没法欺骗Victor（公正性）。

进一步设想一下，如果Victor和Peggy上面的交互过程用摄像机记录下来，然后Victor拿给第三个人Carol看，Carol会相信吗，答案是否定的，因为Peggy和Victor完全可以事先商量好进入哪个通道，从哪个通道出来，这样Peggy在不知道咒语的情况下也可以正确的按照Victor的要求从通道走出来。或许他们不这么做，Peggy走进其中一条通道，Victor发出一个随机的要求，如果Victor猜对了，好极了；如果他猜错了，他们会从录像带中删除这个试验。总之，Victor获得一个记录，它准确显示与实际证明Peggy知道咒语相同的事件顺序。

这就说明了两件事情，其一，Victor不可能 使第三方相信这个证明的有效性；其二，它证明了这个协议是零知识的。在Peggy不知道咒语的情况下，Victor显然不能从记录中获悉任何信息。但是，因为无法区分一个真实的记录和一个伪造的记录，所以Victor不能从实际证明中了解任何信息——它必定是零知识。

谈到这里，大家应该多多少少对零知识证明有个大体的理解。下面给出零知识证明的形式化定义和零知识证明的性质以及基本的零知识协议。

零知识证明的形式化定义

零知识证明定义：知识的证明协议具有零知识性，是指存在一个多项式时间模拟器，能够自行产生一些协议运行的脚本，该脚本与真实脚本有不可区分的概率分布。

怎么理解呢，还是用刚才的例子来说明，我们已经提及Victor没办法让第三方Carol相信，原因就是Peggy和Victor可以模拟Peggy知道咒语的真实情况（存在一个多项式时间模拟器），但是这个真实情况和模拟的情况是没办法区分的（该脚本与真实脚本有不可区分的概率分布）。

零知识证明满足的性质

(1)正确性。P无法欺骗V。换言之，若P不知道一个定理的证明方法，则P使V相信他会证明定理的概率很低。

(2)完备性。V无法欺骗P。若P知道一个定理的证明方法，则P使V以绝对优势的概率相信他能证明。

在零知识协议中，除满足上述两个条件以外，还满足下述的第三个性质。

(3)零知识性。V无法获取任何额外的知识。

这三个性质，在前面的讲解中已经解释了，这里不再赘述。

基本的零知识协议

基本的交互式零知识证明协议的过程如下:

（1）证明者用所知道的信息和一个随机数将这个难题转变成另一难题，新的难题和原来的难题同构。然后用自己的信息和这个随机数解这个新的难题。

（2）证明者利用位承诺方案提交这个新的难题的解法。

（3）证明者向验证者透露这个新难题。验证者不能用这个新难题得到关于原难题或其解法的任何信息。

（4）验证者要求证明者:

(a)向他证明新、旧难题是同构的，或者:

(b)公开证明者在第（2）步中提交的解法并证明是新难题的解法。

（5）证明者同意。

（6）证明者和验证者重复第（1）步至第（5）步 n 次。

非交互式零知识证明

我们在上文提到不能使Carol相信，因为这个协议是交互式的，并且Carol没有介入交互中。为了让Carol和其他感兴趣的人相信，需要一个非交互式的协议。

基本的非交互零知识证明协议 过程如下：

（1）证明者使用他的信息和n 个随机数把这个难题变换成n 个不同的同构难题，然后用他的信息和随机数解决这n 个新难题。

（2）证明者提交这n 个新难题的解法。

（3）证明者把所有这些提交的解法作为一个单向散列函数的输入，然后保存这个单向散列函数输出的前n 个位。

（4）证明者取出在第 3 步中产生的n 个位，针对第i 个新难题依次取出这n个位中的第i 个位，并且：

​ (a)如果它是 0，则证明新旧问题是同构的，或者;

​ (b)如果它是 1，则公布他在第（2）步中提交的解法，并证明它是这个新问题的解法。

（5）证明者将第（2）步中的所有约定及第（4）步中的解法都公之于众。

（6）验证者或者其他感兴趣的人，可以验证第（1）步至第（5）步是否能被正确执行。

这个协议起作用的原因在于单向散列函数扮演一个无偏随机位发生器的角色。如果证明者要进行欺骗，他必须能预测这个单向散列函数的输出。但是，他没有办法强迫这个单向散列函数产生哪些位或猜中它将产生哪些位。这个单 向散列函数在协议中实际上是验证者的代替物—在第（4）步中随机的选择两个证明中的一个。

零知识证明的应用

零知识证明是密码学的一个高级协议，很多问题都有零知识证明的加密方案，但并不是所有问题都有，Goldreich,Micali和Wigderson给出了理论上存在零知识证明解的有效范围。他们发现对于多项式时间内可以验证解的决策问题（问题的答案仅为是/否）存在已知的零知识证明方案。

这里举一个零知识证明的应用——哈密尔顿图的交互式零知识证明和非交互式零知识证明。

哈密尔顿图的交互式零知识证明

哈密尔顿图（Hamiltonian Graph）是图论中的一个重要概念。在一个图中通过每一个顶点一次且仅一次的回路称作哈密尔顿回路。有哈密尔顿回路的图称为哈密尔顿图。现在尚不知道判断一个图是否是哈密尔顿图的充要条件，即使知道判断哈密尔顿图的充要条件，要找到一个具体的哈密尔顿图也是一个难题。

现在的问题是：有一个图 G ，证明者知道这个图的一个哈密尔顿回路。验证者也知道这个图，但不知道这个图的哈密尔顿回路。现在证明者想要在不暴露哈密尔顿回路的条件下，向验证者证明他知道这个图的一个哈密尔顿回路。这个问题的解决方案是什么，零知识证明就派上用场了。

这里有一个事实是：如果证明者知道图G 的一个哈密尔顿回路，那么他也能很容易找出这个图的置换的哈密尔顿回路。

哈密尔顿图的交互式零知识证明如下：

  • 证明者随机地生成图的 G 一个置换H$，并加密H 到H' .

  • 证明者将H' 的副本发送给验证者。

  • 验证者要求证明者证明H' 是图G 的同构副本的加密结果，或者出示H的哈密尔顿回路。

  • 证明者通过解释置换和解密证明H' 是图G 的同构副本的加密结果，但不出示图G ，H的哈密尔顿回路，或者只解密构成哈密尔顿回路的那些边来出示$H$ 的哈密尔顿回路，但不证明图G ,H 同构。

  • 证明者和验证者重复上述过程n次。

在一次协议中，证明者如果不知道图G 的哈密尔顿回路，他最多能做的是创造一个图H 与G 同构，或者创造一个与G 有相同点线的图G' 及其哈密尔顿回路。也就是说，如果证明者不知道图G的哈密尔顿回路，那么他就不可能每次都完成验证者的要求。

完备性：假设证明者是诚实的协议参与者，严格按照协议的步骤执行协议，验证者将以接近 1 的概率接受证明者的证明。

正确性：证明者如果不知道图G的哈密尔顿回路，在每一轮协议中有 frac{1}{2} 的机会欺骗验证者，协议执行n 次以后，证明者欺骗验证者成功的概率为 frac{1}{2^n} ,验证者以 1-frac{1}{2^n} 的概率拒绝证明者的证明。

零知识性：协议完成后，验证者只能得到图 G 的一些随机拷贝或一些不能证明与G 同构的图的哈密尔顿回路，而不能得到图 G的哈密尔顿回路，所以协议是零知识的。

哈密尔顿图的非交互式零知识证明

前面已经提到过交互式的零知识证明无法让第三方相信证明者的结论。所以需要用到非交互式的零知识证明。哈密尔顿图的非交互式零知识证明如下：

（1）证明者随机地生成图G的n个置换 H_i (i=1,2,...,n) ,并加密 H_i 到 H_i' .

（2）证明者将公开所有的 H_i' (i=1,2,...,n) 。

（3）将所有的 H_i' 作为单向散列函数的输入，保存输出结果的前 n 位。

（4）在（3）中所得到的所有的前 n 位中，证明者检查每个输出的第 i 位 (1leq{i} leq {n}) ，作出相应的判断:

  • 若 i=0 ,证明者就证明 H_i' 与图 G 同构。
  • 若 i=1 ,证明者就解密 H_i' ,给出其哈密尔顿回路。

（5）公布（2）~（4）步的过程。

完备性：由单向散列函数的单向输出性，假设证明者是诚实的协议参与者，严格按照协议的步骤执行协议，验证者将以接近 1 的概率接受证明者的证明。

有效性：如果证明者不知道图 G的哈密尔顿回路，他不可能预测单向散列函数的输出。对输出结果前n 位的任一位，证明者猜测成功的概率为 frac{1}{2} ,全部猜测成功的概率为 frac{1}{2^n} ,从而验证者以 1-frac{1}{2^n}

【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/hjs-junyu/p/10686766.html