网易内推题里的合唱团见链接:https://www.nowcoder.com/questionTerminal/661c49118ca241909add3a11c96408c8
我们为了能说清楚动态规划的思路,下面先简化下合唱团的题:
- 给定一个数组a[n],里面的数值代表能量值(都为正数),现在顺序抽取k(k>0)个能量值,约束条件是抽取的相邻能量值所在的索引不能超过d。求抽取k个能量的乘积最大值。
1、明确问题的目标是:
(1)求k个数的最大乘积
(2)相邻索引值差<=d
2、分解问题:
为了求解方便,我们来定个标准,根据k个数的末尾元素把目标问题分为以下n种情况

对以上n种情况比较结果,最后选取最大乘积输出,就是我们要求的目标值了。不过这样我们还需要求出每个结束元素前的k-1个数的最大乘积,这个新问题是不是似曾相识呢?求k-1个数的最大乘积同样又可以以刚才分析的方式去思考,以末尾元素为标准分为几种情况。
那么现在看来为了求目标问题,我们需要明确两个变量的值,一个是末尾元素,另一个是前k-1个最大乘积。因为我们求 k 个数最大乘积依赖于末尾元素和前k-1个数的最大乘积两个因素。我们定义一个二维数组q,行 i 代表末尾元素的索引值,列 j 代表长度。q[i][j] 表示以 a[i] 为末尾元素,长度为 j+1 的最大乘积值。是不是有点抽象了,没关系,接下来会一目了然的。
3、我们先拿个例子走下流程:a[5] = [4,5,2,1,7],k=3,d=2
状态数组q:
j= 0 1 2
i=0 [ [ 4 ]
i=1 [ 5 20 ]
i=2 [ 2 10 40 ]
i=3 [ 1 5 20 ]
i=4 [ 7 14 70 ] ]
(1)先找到初始状态,k=1时,末尾元素为a[i],即q[i][0] = a[i],填充 q 数组。
(2)别忘了,我们有个约束条件,相邻索引值差<=d。假设长度为k的末尾元素索引值为i,它之前长度k-1的最后一个元素索引为p,那么 i-p<=d=2,即 max(i-2,0)=<p<i(i=0除外,因为i=0时末尾元素为a[0],长度只能是1)。
(3)有了初始状态,目标值还会远吗?
接下来看长度 k =2的情况 (即j=1,依赖于j=0的最大乘积和末尾元素),末尾元素为 a[0],长度只能为1,排除。
末尾元素为 a[1],前一个元素索引范围 0=<p<1,观察图1,前1个数最大乘积只能为 4。即q[1][1] = 4 * a[1] = 20 。
末尾元素为 a[2],前一个元素索引范围 0=<p<2,观察图2,前1个数最大乘积=max(4,5),即q[2][1] = 5*a[2] = 10。
末尾元素为 a[3],前一个元素索引范围 1=<p<3,观察图3,前1个数最大乘积=max(5,2),即q[3][1] = 5*a[3] = 5。
末尾元素为 a[4],前一个元素索引范围 2=<p<4,观察图4,前1个数最大乘积=max(2,1),即q[4][1] = 2*a[4] = 14。
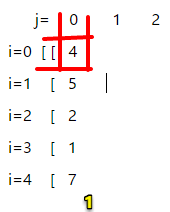
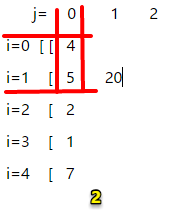
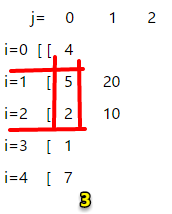
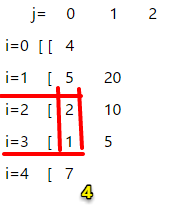
(4)加油,还差一点点,你就成功了。
接下来看长度 k =3 (即j=2,依赖于j=1的最大乘积和末尾元素),末尾元素为 a[0],长度只能为1,排除。
末尾元素为 a[1],长度最多为2,排除。
末尾元素为 a[2],前一个元素索引范围 0=<p<2,p只能为1,观察图5,前2个数的最大乘积只能为20,所以q[2][2] = 20*a[2] = 40。
末尾元素为 a[3],前一个元素索引范围 1=<p<3,观察图6,前2个数的最大乘积=max(20,10),所以q[3][2] = 20*a[3] = 20。
末尾元素为 a[4],前一个元素索引范围 2=<p<4,观察图7,前2个数的最大乘积=max(10,5),所以q[4][2] = 10*a[4] = 70。

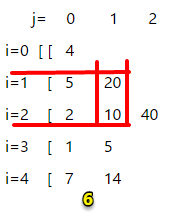
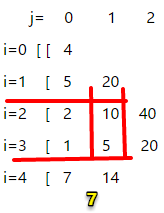
以上我们把状态数组q全部求出来了,不要因为走的太远而忘记为什么出发,我们的目标是比较末尾元素为a[i]的长度为k的最大乘积。那就比较q[i][2],得出70是以a[4]为末尾元素的长度为3的最大乘积。大致的思路就是这些了,原来求 k 个数的最大乘积要回溯到 k=1 时初始状态一步步求解啊。
搞明白了思路,代码也就出来了。就这个例子而言,代码如下:
1 #coding:utf-8 2 a = [4,5,2,1,7] 3 k = 3 4 d = 2 5 n = len(a) 6 q = [[0 for j in range(k)] for i in range(n)] 7 #j代表列 i代表行 对状态数组q赋值 8 value = 0 9 for j in range(k): 10 for i in range(n): 11 #初始化第0列 12 if j == 0: 13 q[i][j] = a[i] 14 continue 15 for l in range(max(0,i-d),i): 16 q[i][j] = max(q[i][j], q[l][j-1]*a[i]) 17 if j == k-1: 18 value = max(value, q[i][j]) 19 print value
4、下面我们来总结动态规划
实际上动态规划问题都可以用递归来求解,不过递归的时候会求重复项并且造成栈溢出问题,所以我们借助状态数组把每个状态(递归返回值 )记录下来,用自底而下的思想去求解目标问题,从递归的边界条件出发求得动态规划的初始状态,然后一步步求解目标,相当于递归的逆过程。
动规解题的一般思路
(1) 原问题分解为子问题
-
把原问题分解为若干个子问题,子问题和原问题形式相同或类似,只不过规模变小了。子问题从初始状态开始解决。
-
子问题的解一旦求出就会被保存,所以每个子问题只需求解一次。
(2)确定状态
-
在用动态规划解题时,我们往往将和子问题相关的各个变量的一组取值,称之为一个“状态”。一个“状态”对应于一个或多个子问题, 所谓某个“状态”下的“值”,就是这个“状 态”所对应的子问题的解。
-
所有“状态”的集合,构成问题的“状态空间”。“状态空间”的大小,与用动态规划解决问题的时间复杂度直接相关。 在数字三角形的例子里,一共有N×(N+1)/2个数字,所以这个问题的状态空间里一共就有N×(N+1)/2个状态。
整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。
(3)确定一些初始状态(边界状态)的值
以上面为例,就是求解q数组第一列的值。
(4) 确定状态转移方程
定义出什么是“状态”,以及在该“状态”下的“值”后,就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的 “状态”,求出另一个“状态”的“值”(递推型)。状态的迁移可以用递推公式表示,此递推公式也可被称作“状态转移方程”。
特点:
1>问题具有最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质。
2>无后效性。当前的若干个状态值一旦确定,则此后过程的演变就只和这若干个状态的值有关,和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态,没有关系。
引申:想到HMM里的维特比算法也是利用动态规划求解最短路径,有必要再加强学习下!
参考:http://blog.csdn.net/baidu_28312631/article/details/47418773