树链剖分入门讲解
问题导入
当我们做题目的时候,往往会有一些题目是给定一颗树,并对这颗树做一堆蛇皮怪物般的操作的。
比如:
1.询问x到y路径上的最小最大最¥#%¥#@¥@#¥值
2.询问x到y路径上的xor,和,乘@!#¥@#¥%¥#值
3.纯模拟是过不了的且往往与lca挂钩
4.没有动态的加边删边23333
5.往往下面还要接一个线段树
那么,我们要怎么做呢?
这里提供一种思想,就是把树拆掉:
以轻重边为基础的拆边,把一颗树拆成大大小小的几条链放到类似于常用的线段树里面加以操作。
轻重边
在树链剖分里,我们定义如下规则
1.重儿子:当前节点的儿子节点中子树大小最大的那一个
2.轻儿子:当前节点除了重儿子以外的所有节点
那么
重链即为重儿子连成的链,轻链即为轻儿子连成的链。
.png)
我们可以通过这张图看到如下分链解释
节点1的儿子(2,3)中2的子树大小更大所以选取2为重儿子。
节点6的儿子(7,9)中7的子树大小更大所以选取7为重儿子。
但是并不是轻儿子后面就一定是一直是轻链的,比如节点4后面就又接了一条重链。
我们可以这样理解,当一个节点选取了一个重儿子以后,它其他的轻儿子节点就重新开始,按照之前的规则选择它的轻重儿子。
我们可以观察到,重链上的任意两点之间的路径是不是都在这条重链上,可以化成链直接在线段树上调用了。
且还有如下两个性质
1.轻边(u,v)中, size(u)≤ size(u/2)
2.从根到某一点的路径上,不超过logn条轻链和不超过logn条重链。
(蒟蒻表示并不会证)
其实我们在这里还能发现如果要统计一个点的轻重儿子,是不是还能顺便处理出它的子树size。
那么我们要怎么处理出重儿子和轻儿子呢?DFS序。
void dfs1(int x) //这个是用来求一个节点的子树大小的,即顺便求出轻重儿子
{
size[x]=1; //当前这个点本身大小为1
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
if(!dep[v])
//其实这里的if里面也可以这么写if(v!=fa[x])
{
dep[v]=dep[x]+1;
fa[v]=x;//一般都是双向边,然后是为了跳lca
dfs1(v);
size[x]+=size[v];
if(size[v]>size[son[x]])son[x]=v; //求出重儿子
}
}
}
DFS序
(以下内容引至洛谷讲义)
我们DFS一棵树的时候,对这棵树的每个点按照访问的时间进行重标号,就得到了树的DFS序列。 这个序列可以有效地处理一些树上的问题。 如图就是一棵树的一种可能的DFS序
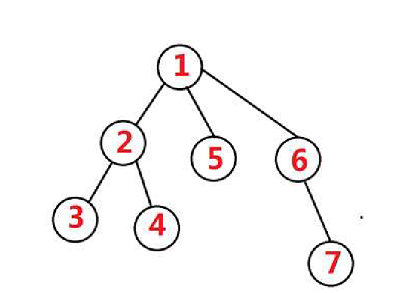
记录DFS的时候每个点访问起始时间与结束时间,记最起始时间是前序遍历,结束时间是后序遍历。可以发现树的一棵子树在DFS序上是连续的一段
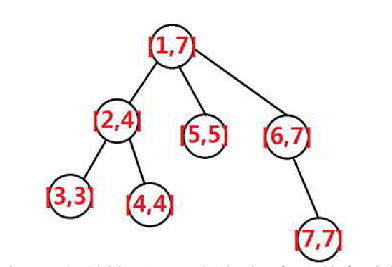
如图, DFS之后,那么树的每个节点就具有了区间的性质。那么此时,每个节点对应了一个区间,而且可以看到,每个节点对应的区间正好“管辖”了它子树所有节点的区间,那么对点或子树的操作就转化为了对区间的操作。
蒟蒻的一句话总结
以一个节点为起点,不往回走,一直搜到它能到达的所有点,优先走重儿子,轻儿子等重儿子走完以后回溯上来再往下走。
而每个点的dfs序就是它按顺序被搜到的时间点(前面有多少个点已经被搜过了)。
void dfs2(int x,int t)
{
//l[]表示这个点的dfs序
//然后a[]是以dfs序为下标(维护链)的当前点的点值
//ch[]是题目给出的点值
//top[]记录的是这个点所在的链的顶端的那个点,用来跳lca
l[x]=++tot;a[tot]=ch[x];top[x]=t;
if(son[x])dfs2(son[x],t); //有重儿子维护重链
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
if(v!=fa[x]&&v!=son[x])
//不是父亲不是重儿子,以轻儿子为端点的新链dfs下去
dfs2(v,v);
}
}
LCA
当我们把当前的树剖成了链以后,我们要怎么做呢?
一个一个访问显然是不可能的,有倍增法跳lca的例子在前,我们是不是也可以模仿呢?
首先我们要搞清楚链是怎么下放到线段树上去的。
以某个点为例,先把这个点的一条重链下放,在回溯过程中搜索以其他轻儿子为顶端的重链下放。所以在线段树中存的点的顺序便是节点的dfs序值。
当我们把一颗树剖成链以后我们可以注意到如下特点
1.如果要询问以x的子树信息,在之前求轻重链的时候我们已经维护好了x的size大小,然后根据dfs序的遍历特点,我们可以得出如果是关于子树的操作,就是在线段树上询问 l[表示dfs序的数组] + size[当前节点]-1 ,-1是因为它本身重复算了两次。这样看来子树在线段树上是一段连续的区间,这样是不需要跳lca的。
2.我们发现x到y上的路径可能会经过几条重链和轻链,而它们并不一定在线段树上是连续的一段,那么这样的话我们就需要依次维护这几条链了,也就是说我们用可以跳链的方法一边进行维护一边跳lca。
那么我们要怎么进行跳链维护呢?
这个算法很明显的是用来节约时间的算法。
是不是我们就可以这么想:
既然以x的子树信息可以直接调用,又x到这条重链上的任一一点在线段树上都是一段连续的区间。那么x到y的路径就是通过x和y不断的从自身的链往上跳,一次跳一条重链因为重链在线段树上可以直接维护。然后就是要清楚当前x和y谁的top节点深度更深,因为跳深度低的可能会错过lca。那么跳链的方法就出来了。
让我们再以这张图为例
.png)
我们现在要让10和5跳lca。很明显我们要从10跳到4,因为5会直接跳到1而它们的lca很明显是2。
下面我们贴出一个给x到y路径加值的代码
void cal2(int x,int y,int v)
{
int fx=top[x],fy=top[y];
while(fx!=fy)//如果顶点相同了就不用跳了直接在线段树上下放
{
//按上面说的判断top深度
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
update(1,1,tot,l[fx],l[x],v);
x=fa[fx],fx=top[x];
//x换到另一条链继续往上跳
}
if(l[x]>l[y])swap(x,y);
//在这里dfs序和dep之间是没有区别的
//因为深度深的点在同一条重链里很明显是后被dfs到的
update(1,1,tot,l[x],l[y],v);
}
模板
这样的话我们就说完了树链剖分的基本思路
下面贴出洛谷的模板
P3384 【模板】树链剖分
题意
给定一颗树维护它的子树和路径加值问题。可以说是非常模板了。
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<iostream>
#define ll long long
using namespace std;
struct node{
ll to,next;
}e[500001];
ll rt,mod;
ll head[500001],dep[500001],sum[500001],a[500001];
ll tot,num,n,m,lazy[500001],fa[500001],l[500001];
ll ch[500001],top[500001],size[500001],son[500001];
void build(int root,int l,int r)
{
if(l==r){sum[root]=a[l];return ;}
int mid=(l+r)>>1;
build(root<<1,l,mid);
build(root<<1|1,mid+1,r);
sum[root]=sum[root<<1]+sum[root<<1|1];sum[root]%=mod;
return ;
}
void push(int root,int l,int r)
{
int mid=(l+r)>>1;
lazy[root<<1]+=lazy[root];lazy[root<<1]%=mod;
lazy[root<<1|1]+=lazy[root];lazy[root<<1|1]%=mod;
sum[root<<1]+=lazy[root]*(mid-l+1);sum[root<<1]%=mod;
sum[root<<1|1]+=lazy[root]*(r-mid);sum[root<<1|1]%=mod;
lazy[root]=0;
return ;
}
void update(int root,int left,int right,int l,int r,ll k)
{
if(l<=left&&r>=right)
{
sum[root]+=k*(right-left+1);sum[root]%=mod;
lazy[root]+=k;lazy[root]%=mod;
return;
}
if(left>r||right<l)return ;
int mid=(left+right)>>1;
if(lazy[root])push(root,left,right);
if(mid>=l)update(root<<1,left,mid,l,r,k);
if(mid<r) update(root<<1|1,mid+1,right,l,r,k);
sum[root]=(sum[root<<1|1]+sum[root<<1])%mod;
return;
}
ll query(int root,int left,int right,int l,int r)
{
if(l<=left&&r>=right)return sum[root]%mod;
if(left>r||right<l)return 0;
int mid=(left+right)>>1;
if(lazy[root])push(root,left,right);
ll a=0,b=0;
if(mid>=l) a=query(root<<1,left,mid,l,r);
if(mid<r) b=query(root<<1|1,mid+1,right,l,r);
return (a%mod+b%mod)%mod;
}
--------------------以上是线段树分割线-------------------------
void dfs1(int x)
{
size[x]=1;
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
if(!dep[v])
{
dep[v]=dep[x]+1;
fa[v]=x;
dfs1(v);
size[x]+=size[v];
if(size[v]>size[son[x]])son[x]=v;
}
}
}
void dfs2(int x,int t)
{
l[x]=++tot;a[tot]=ch[x];top[x]=t;
if(son[x])dfs2(son[x],t);
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
if(v!=fa[x]&&v!=son[x])
dfs2(v,v);
}
return ;
}
ll cal1(int x,int y)//查询路径值
{
ll maxx=0;
int fx=top[x],fy=top[y];
while(fx!=fy)
{
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
maxx+=query(1,1,tot,l[fx],l[x]);
x=fa[fx];fx=top[x];
}
if(l[x]>l[y])swap(x,y);
maxx+=query(1,1,tot,l[x],l[y]);
return maxx;
}
void cal2(int x,int y,int v)//维护路径加值
{
int fx=top[x],fy=top[y];
while(fx!=fy)
{
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
update(1,1,tot,l[fx],l[x],v);
x=fa[fx],fx=top[x];
}
if(l[x]>l[y])swap(x,y);
update(1,1,tot,l[x],l[y],v);
}
ll read()
{
ll x=0,w=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*w;
}
void add(int from,int to)
{
num++;
e[num].to=to;
e[num].next=head[from];
head[from]=num;
}
int main()
{
n=read();m=read();rt=read();mod=read();
for(int i=1;i<=n;i++)ch[i]=read(),ch[i]%=mod;
for(int i=1;i<n;i++)
{
int x=read(),y=read();
add(x,y);add(y,x);
}
dep[rt]=1;fa[rt]=1;
dfs1(rt);dfs2(rt,rt);build(1,1,n);
while(m--)
{
int qwq=read();
if(qwq==1){int x=read(),y=read(),z=read();cal2(x,y,z%mod);}
if(qwq==2){int x=read(),y=read();printf("%lld
",cal1(x,y)%mod);}
if(qwq==3){int x=read(),y=read();update(1,1,n,l[x],l[x]+size[x]-1,y%mod);}
if(qwq==4){int x=read();printf("%lld
",query(1,1,n,l[x],l[x]+size[x]-1)%mod);}
//子树可以直接调用
}
return 0;
}
好了到此模板就教完了,我们来讲一点关于树链剖分有意思的题目。
顺便提一句
考树链剖分不是考剖分而是考线段树!!!!
关于树链剖分基本操作的模板题
【 题解 】 P3178 [HAOI2015]树上操作
【 题解 】P2590 [ZJOI2008]树的统计
【 题解 】P2146 [NOI2015]软件包管理器]
这里的每一道题都是维护子树和路径的,甚至不需要什么思路,只要会一点点树链剖分的板子就可以了233333333,打完就入门了。
边转点问题
有时候我们会看到这样一些题目,它们不会给定每个点的值,而是给定每条路径的值,这样我们又要如何维护呢?
首先思考一波拆边,像lct那样的,弃疗了
后来某YZK大佬安利我一句,从下往上跳lca又儿子到父亲只有一条边,是不是就可以把边权值给那个点的儿子节点呢,因为给一个父亲的话,父亲是不是会有几个儿子,值就会混乱,但是儿子只有一个父亲,就o**k了。
在这里狂膜%%%%%YZK大佬
果然吊打我几万里。
所以做这类问题的思路便出来了,我们考虑把每一条边的值赋给它的儿子节点,注意这样在跳lca的时候,lca的值是要减去的,因为它的值是它到它父亲的边权,不包括在这次跳链的过程中。
建议不懂的画个图理解一下emmm。
就不给图了略略略略
给一道比较好做的模板题
【 题解 】P3038 [USACO11DEC]牧草种植Grass Planting
多重建树问题
做过永无乡的julao们应该都知道,在维护每一个联通块的时候,我们都要以一个节点单独建splay。然后lct中维护颜色联通块时,也有类似思想。
那么是不是能把这个思想运用到树剖上呢?
让我们来分析一下下列问题。
一条路径上,每次询问的是同一条路径,但是这条路径维护了几个不同的信息。
这里的不同的信息指的是,比如:这一条路径有几个不同的属性,我每次能查询或修改随机的一个属性,这时候我们就要保存每个属性来提供答案。
那么当我们观察到这个有关属性是一个小范围的值的时候,我们就可以考虑一手维护多个线段树,注意一般不是建多条链,而是把根据一条链的几个属性分别建树,然后按照对应的属性在那个线段树上查询。
一般思想不难,就是难调咕咕咕
经典例题:
BJOI2018求和
它要维护一个数的k次方,而k<=50
这样我们就可以思考把每一个次方放到一颗对应的线段树去维护。
调了我两天qaq(我果然是太菜了)
【 题解 】P4427 [BJOI2018]求和
博主(caiji)自己yy的操作
有时候学东西学多了,就会开始不经意的思考 (作死)
至于怎么作死呢,当时博主在学分块emmm,是的,自己在yy树上分块
毕竟同样是把树链下放,下放到什么样的数据结构不随便我们自己吗。。。那么我们岂不是就可以开始操作(作死)了
比如像这样一个题目(YYJ的原创题)
题目描述:
Brave_cattle学姐,
当我来到这个世界的时候,我不知道我曾会遇见你。
在这个世界即将要毁灭的边缘,
我们又还能在一起做些什么? 还能在躺在草地上吗?
想着曾经的点点星空,原来,时间过得是这么的快啊。
在生命终结的时候,
让我们再看着星空死去吧。
嗯? 为什么此时此刻的星空有点奇怪?
宛如星座一般的边把星星怎么连成了一棵树?
怎么,那不是星星!是即将砸过来的陨石!
某个时刻,x 到 y 的路径上的星星靠近度又增加了 z。
某个时刻,我们需要知道 x 到 y 的路径上的星星的靠近度大于等于 z 的数量。
刻不容缓。 末日就要到了。
输入
第一行 n 个点,m 个时刻 第二行 给定 1—n 个点的靠近度
接下来 n-1 行 表示 x 和 y 有一条连边 接下来 m 行表示 m 个时刻 每个时刻有两种情况
Q x y z 表示询问 x 到 y 的路径上的星星的靠近度大于等于 z 的数
M x y z 表示 x 到 y 的路径上的星星靠近度又增加了 z
输出
需要对每个 Q 的时刻进行回答
样例 输入
10 5
1 2 3 4 5 6 7 8 9 10
1 2
1 3
3 5
3 6
2 4
4 7
4 8
8 10
8 9
Q 1 10 4
M 1 9 3
M 1 10 1
Q 1 7 9
Q 1 7 8
输出
3
0
1
数据范围
第 1,2 个点
1<=n,m<=500 1<=靠近度值<=10^4
第 3,4,5,6,7,8,9,10 个点
1<=n<=1000000,1<=m<=5000,1<=靠近度值<=10^6
ps:数据保证靠近度值不超过 int
博客没事干搞出来的 (浪费时间没有难度的题目)难题
后面因为树的中心靠上且没有生成较长的链,别人轻松模拟比正解快三倍,身败名裂
所以这个题目要怎么写呢,
权值线段树+树链剖分????貌似可以这么写
反正我写的是分块加树链剖分
原题是教主的魔法,我只是把它压到树上了
所以就是先按教主的魔法打好,然后在按树剖后的dfs序下放进去,julao们告诉我这太麻烦了????反正我太菜了,其他骚操作又没学
就是在你没学习欧拉序的情况下,
麻烦一点强行树上分块,时间复杂度在分块的基础上再加上一个log
好了,树链剖分加分块已经有了:
主席树加树链剖分还会远吗?
单调队列加树链剖分还会远吗?
莫队加树链剖分还会远吗?(虽然有树上莫队来着)