------------恢复内容开始------------
https://blog.csdn.net/wang3312362136/article/details/80615874基本解释
模板可以看下面这道难题:
hdu5575:
题目大意:
有一个1维的长度为N,高度无限的水柜,现在要用N-1个挡板将其分为N个长度为1的小格,然后向水柜中注水,水可以低于挡板也可以以溢出去(这样就要与旁边格子的水位相同),现在有M次探测,探测i,y,k为查询第i个格子高度y+0.5处是否有水,k=1表示有水,k=0表示没有水,这M次探测不保证结果正确,现求结果正确个数的最大可能值。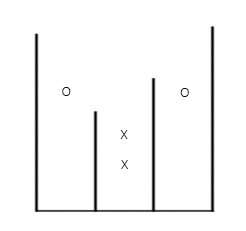
首先,直觉告诉我们当水箱中没有水时, z=0z=0 的询问(以下简称为X,而 z=1z=1 的询问简称为O)的个数就是答案。但是当水箱中有水时,可能还会得到更优的答案。因此我们可以以X的个数为初始答案,通过不断改变水箱的水位来更新答案 ansans 的值。那么应该以什么样的顺序来改变水位呢?显然应该由低到高改变水位,因此我们将O存储到一个数组(这里用的是向量)中并排序,以备后面按顺序枚举。现在假设我们枚举到第i个O,我们需要知道水位向左能溢出到多远向右能溢出到多远。这通过两个循环就能够判断。接下来我们要对当前的O溢出到的每个小水箱x执行以下操作:询问在当前水位高度 hh 下有多少X,有多少O。O的数量减X的数量的差值 dd 就可以用来更新 ansans 了: ans+=dans+=d 。思路大体上是这样,实现起来却会遇上很多问题。首先是每次枚举O的时候向左向右溢出都有 O(n)O(n) 的复杂度。当水向左向右溢出以后,实际上O溢出到的小水箱能够合并成一个大水箱这样 O(m)O(m) 次枚举O的复杂度就是 O(n)O(n) 而不是 O(nm)O(nm) 了。要高效地查询和合并,我们可以用并查集来维护每个由小水箱合并而成的大水箱。具体地,合并的时候不仅要合并当前水位之下的O和X的数量,还要维护大水箱的左右两边是哪些水箱以及是哪些挡板。O的数量可以看当前枚举了多少O,X的数量可以用某个能够维护顺序的数据结构来维护,这个数据结构维护结构体 (x,y)(x,y) ,结构体表示的这个X在坐标为 (x,y)(x,y) 的位置。那么我们在计算 xx 小水箱的水位 hh 下的X的时候,就可以在删除数据结构最小元素的同时计数,直到 y≥hy≥h 即最低位置的X在水位之上了为止。维护顺序的数据结构可以用堆或者平衡树,但是又需要数据能够快速地合并,因此使用由左偏树实现的可并堆是最合适不过了。
总而言之就是以z = 0的询问总数为初始答案,通过枚举z = 1的询问来更新答案,用并查集维护水箱并处理水箱的合并。用由左偏树实现的可并堆来处理水箱的合并及计算单次枚举的答案(涉及查询最小值及删除最小值)。
最后的本题总的复杂度应该是O(n + mlog(m))。截止本题的解题报告写成时HDU上本题用时排名前五的算法都是由下面的代码提交达成的。
#include <bits/stdc++.h>
using namespace std;
typedef pair <int, int> query;
const int maxn = 1e5 + 10, maxm = 2e5 + 5;
int t, n, m, x, y, z, ans;
int L[maxn], R[maxn], LH[maxn], RH[maxn], O[maxn], X[maxn];
vector <query> vec;
// 左偏树相关
int tot, v[maxm], l[maxm], r[maxm], d[maxm], Heap[maxn];
// 合并左偏树
int merge(int x, int y) {
if(x == 0) {
return y;
}
if(y == 0) {
return x;
}
if(v[x] > v[y]) {
swap(x, y);
}
r[x] = merge(r[x], y);
if(d[l[x]] < d[r[x]]) {
swap(l[x], r[x]);
}
d[x] = d[r[x]] + 1;
return x;
}
// 初始化可并堆结点
inline int init(int x) {
v[++tot] = x;
l[tot] = r[tot] = d[tot] = 0;
return tot;
}
// 左偏树的插入操作
inline int insert(int x, int y) {
return merge(x, init(y));
}
// 取得左偏树中的最小值
inline int top(int x) {
return v[x];
}
// 弹出左偏树
inline int pop(int x) {
return merge(l[x], r[x]);
}
// 判断左偏树是否非空
inline bool empty(int x) {
return x == 0;
}
// 初始化可并堆
void initHeap() {
memset(Heap, 0, sizeof(Heap));
tot = 0;
}
// 并查集相关
int p[maxn];
// 初始化并查集
void initSet() {
for(int i = 1; i <= n; i++) {
p[i] = i;
}
}
// 查找集合的祖先
int find(int x) {
return x == p[x] ? x : p[x] = find(p[x]);
}
// 合并集合
inline void Union(int x, int y) {
x = find(x);
y = find(y);
if(x == y) {
return;
}
p[y] = x;
if(x < y) {
RH[x] = RH[y];
L[R[x]] = x;
R[x] = R[y];
}
else {
LH[x] = LH[y];
R[L[x]] = x;
L[x] = L[y];
}
// 合并可并堆
Heap[x] = merge(Heap[x], Heap[y]);
X[x] += X[y];
O[x] += O[y];
}
int main() {
scanf("%d", &t);
for(int c = 1; c <= t; c++) {
scanf("%d%d", &n, &m);
LH[1] = RH[n] = INT_MAX;
L[n] = n - 1;
for(int i = 1; i < n; i++) {
scanf("%d", &RH[i]);
// 用于快速查询水箱的左右挡板
LH[i+1] = RH[i];
// 用于快速查询左右方水箱
L[i] = i - 1;
R[i] = i + 1;
}
initHeap();
vec.clear();
ans = 0;
while(m--) {
scanf("%d%d%d", &x, &y, &z);
if(z == 1) {
vec.push_back(query(y + 1, x));
}
else {
Heap[x] = Heap[x] ? insert(Heap[x], y) : init(y);
ans++;
}
}
initSet();
sort(vec.begin(), vec.end());
for(int i = 1; i <= n; i++) {
O[i] = X[i] = 0;
}
for(int i = 0; i < vec.size(); i++) {
x = find(vec[i].second);
y = vec[i].first;
// 向左溢出
while(y > LH[x]) {
Union(x, L[x]);
x = find(x);
}
// 向右溢出
while(y > RH[x]) {
Union(x, R[x]);
x = find(x);
}
// 删除水位以下的X
while(!empty(Heap[x]) && top(Heap[x]) < y) {
Heap[x] = pop(Heap[x]);
X[x]++;
}
// 更新答案
if(++O[x] >= X[x]) {
ans += (O[x] - X[x]);
O[x] = X[x] = 0;
}
}
printf("Case #%d: %d\n", c, ans);
}
return 0;
}
洛谷 攻占城池
用左偏树的思想从底部不断到上面来
#include<cstdio>
#include<algorithm>
#include<math.h>
#include<string.h>
using namespace std;
typedef long long ll;
const ll maxn=3e5+10;
ll flag[maxn],base[maxn]; //城池的val更新方式
ll ch[maxn][2]; //子节点
ll val[maxn],guishu[maxn]; //将领的战力值和第一个城池
ll root[maxn]; //每一个城池的根节点;
ll dep[maxn],dis[maxn]; //dep是用来计算将领的攻占城池数量的, dis是左偏树的深度;
ll ans1[maxn],ans2[maxn]; //城池答案,将领答案;
ll mul[maxn],add[maxn]; //懒惰标记
ll limit[maxn]; //城池耐久值
struct node //邻接表
{
ll v,next;
}G[maxn]; ll head[maxn];ll num=-1;
void build(ll u,ll v)
{
G[++num].v=v;G[num].next=head[u];head[u]=num;
}
void cov(ll x,ll c,ll j)
{
if(!x) return;
val[x]*=c;val[x]+=j; //这里有一个乘和一个加,自然是先乘后加; 这是根据下文这两句来确定的
mul[x]*=c; //这里的确定方式是将已经有的懒惰节点的值与本次加进来的懒惰节点更新;
//已经有的,自然那些要+的,也要乘上这次的数,然后再加上这次要加的数
//注:下次看这里看不懂的话,多看一下肯定会懂的
add[x]*=c;add[x]+=j;
}
void pushdown(ll x)
{ //左右儿子都得更新
cov(ch[x][0],mul[x],add[x]);
cov(ch[x][1],mul[x],add[x]);
mul[x]=1;add[x]=0;
}
ll Merge(ll x,ll y)
{
if(!x||!y) return x+y;
pushdown(x);pushdown(y);//顺便说下每个pushdown为什么要放在这里,首先这里合并一个新的树过来肯定要里面先把该父亲点的信息往下传,鬼知道你合并个新东西进来取代了原来的儿子,他儿子跑别的地方去了就继承不了了
if(val[x]>val[y]) swap(x,y);
ch[x][1]=Merge(ch[x][1],y);
if(dis[ch[x][0]]<dis[ch[x][1]]) swap(ch[x][0],ch[x][1]);
dis[x]=dis[ch[x][1]]+1;
return x;
}
void dfs(ll u,ll fa)
{
dep[u]=dep[fa]+1;
for(ll i=head[u];i!=-1;i=G[i].next){
ll v=G[i].v;
dfs(v,u);
root[u]=Merge(root[u],root[v]);
}
while(root[u]&&val[root[u]]<limit[u]){
pushdown(root[u]);//这里也是要的因为该老人家战败了,接下来轮到他儿子上场比较了,就得先把信息传下去,老人家才好安息
ans1[u]++;//这个就是战败的直接+1;
ans2[root[u]]=dep[guishu[root[u]]]-dep[u];//在这里战败了可以记录多少个城市了
ll t=root[u];
root[u]=Merge(ch[t][0],ch[t][1]);
}
if(flag[u]) cov(root[u],base[u],0);//while一遍后就是第一个可以过该城的士兵,根据左偏树的性质他后面的士兵也可以过去,由于一个一个更新肯定会爆炸,我们运用懒惰标记法
else cov(root[u],1,base[u]);
}
int main()
{
ll n,m;
memset(head,-1,sizeof(head));
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++) scanf("%lld",&limit[i]);
for(ll i=2;i<=n;i++){
ll u;
scanf("%lld%lld%lld",&u,&flag[i],&base[i]);
build(u,i);
}
for(ll i=1;i<=m;i++){
scanf("%lld%lld",&val[i],&guishu[i]);
ll t=guishu[i];
mul[i]=1;
if(!root[t]) root[t]=i;
else root[t]=Merge(root[t],i);
}
dfs(1,0);
while(root[1]){
pushdown(root[1]);
ans2[root[1]]=dep[guishu[root[1]]];
root[1]=Merge(ch[root[1]][0],ch[root[1]][1]);
}
for(ll i=1;i<=n;i++) printf("%lld\n",ans1[i]);
for(ll i=1;i<=n;i++) printf("%lld\n",ans2[i]);
return 0;
}
洛谷的光滑数
洛谷讲的挺好搬过来!!!
首先我们要发现一个性质,就是最大的伪光滑数所有质因数相同。如果一个合法的伪光滑数有不相同的质因数,我们把小的质因数全部换成最大的,需要满足的式子中,k没有变化,所以这个数仍旧合法,却比原来的数大。
观察到要求的第K大的K较小,那么我们用堆维护。每次取出最大值,如果这个数最大质因数的幂次大于1,那么把其中一个最大质因数换成较小的扔进堆里。由于最大质因数和分解的项数k不变,所以始终满足a。同时也很容易发现这样枚举是没有遗漏和重复的。
#include<bits/stdc++.h>
#define ts cout<<"ok"<<endl
#define int long long
#define hh puts("")
#define pc putchar
//#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
//char buf[1<<21],*p1=buf,*p2=buf;
using namespace std;
int n,k;
int pr[105]={0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,
59,61,67,71,73,79,83,89,97,101,103,107,109,113,127};//31个
struct node{
int val,p,mi,lim;//值,最大质数,幂次,下个数的限制
friend bool operator < (node A,node B){
return A.val<B.val;
}
};
priority_queue<node> q;
inline int read(){
int ret=0,ff=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') ff=-1;ch=getchar();}
while(isdigit(ch)){ret=ret*10+(ch^48);ch=getchar();}
return ret*ff;
}
void write(int x){if(x<0){x=-x,pc('-');}if(x>9) write(x/10);pc(x%10+48);}
void writeln(int x){write(x),hh;}
void writesp(int x){write(x),pc(' ');}
signed main(){
n=read(),k=read();
for(int i=1;i<=31;i++){
int now=pr[i];
for(int j=1;now<=n;j++,now=now*pr[i])
q.push((node){now,pr[i],j,i-1});
}
while(k--){
node now=q.top();
q.pop();
if(!k){
write(now.val);
return 0;
}
if(now.mi>1)
for(int i=1;i<=now.lim;i++)
q.push((node){now.val/now.p*pr[i],now.p,now.mi-1,i});
}
return 0;
}
poj 3666
给你一个序列,将序列变为不严格的上升序列或者下降序列都可以,每次操作是对一个数字+1或-1,求最少操作次数.
对于一个非递减序列,最小代价是把每个数都变成这个序列的中位数。
所以我们的序列可以发现就是有上升有下降的序列,最粗糙的想法就是每个单调区间自己找到自己的中位数,w[i],但是我们发现仅仅这样肯定不满足单调,故我们对每个区间进行合并。
例如我们已经w[1]<=w[2]<=w[3]。。。接下来来了个w[4]但这个w[4]<w[3],所以我们需要将w【3】和w【4】的两个区间合并找到一个新的中位数w【3】,然后继续和w【2】比较,知道满足单掉为止。
我们发现合并之后的w【3】是不可能大于原本的w【3】的,也就是从小于这个中位数的里面找,也就是从w【3】,w【4】里的,再加上“合并”。我们可以联想到左偏树。
左偏树维护最大堆+个数限制,那么堆顶就是中位数,(例如5个元素,(5+1)/2=3,第三个元素是中位数)
然后合并不单调的。
大体思想是:用左边树保存每一段部分的中位数。
把每个数单独建一颗左偏树。因为只有一个数,当然中位数是自己。
树里面只保存(len+1)/2个节点,len为这课左偏树所管理的长度(即影响范围)。
然后从左往右扫,一旦扫到后面的中位数比前面的中位数要小,就把这两棵树合并。
这时候一个很关键的操作,弹去树根:这是保证左偏树保存的是中位数的重要操作。
原来,左偏树只保存了len长度范围内,前(len+1)/2的元素(按大小排序)。
一个影响范围为lena的左偏树,与一个影响范围为lenb的左偏树,合并之后,只会保存(lena+lenb+1)/2个节点;
前者已经存了(lena+1)/2个节点,后者为(lenb+1)/2。
直接合并,会得到一个节点总数为(lena+1)/2+(lenb+1)/2的树。
如果(lena+lenb+1)/2小于(lena+1)/2+(lenb+1)/2,则弹去树根(最大值)。
易得(lena+1)/2+(lenb+1)/2最多只比(lena+lenb+1)/2大1,所以只需删去一个节点,即最大的那个节点.
#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
using namespace std;
#define MAXN 2010
#define LL long long
#define min(a, b) (a < b ? a : b)
struct Node
{
int v, l, r, dis;
Node() {}
Node(int _v, int _l, int _r, int _d):
v(_v), l(_l), r(_r), dis(_d) {}
}nn[2][MAXN];
int merge(Node n[], int x, int y)
{
if(!x) return y;
if(!y) return x;
if(n[x].v < n[y].v) swap(x, y);
n[x].r = merge(n, n[x].r, y);
if(n[n[x].l].dis < n[n[x].r].dis) swap(n[x].l, n[x].r);
n[x].dis = n[n[x].r].dis + 1;
return x;
}
int N, v[MAXN], len[MAXN], stk[MAXN];
LL ans[2];
void solve(Node n[], int t)
{
int top = 0;
for(int i = 0; i < N; i++)
{
int ct = 1; int id = i;
while(top > 0 && n[stk[top - 1]].v > n[id].v)
{
top--;
id = merge(n, stk[top], id);
if((len[top] + 1) / 2 + (ct + 1) / 2 > (len[top] + ct + 1) / 2)///首先len是保存的是这个左偏树所控制的范围,但左偏树本身只保留到(len+1)/2个,也就是堆顶刚好是中位数,所以合并的时候如果这两颗左偏树的点大于他所控制的范围,就弹出一个
id = merge(n, n[id].l, n[id].r);
ct += len[top];
}
len[top] = ct;
stk[top++] = id;
}
for(int i = 0, j = 0; i < top; i++)
{
int k = n[stk[i]].v;
while(len[i]--) ans[t] += abs(v[j++] - k);
}
}
int main()
{
// freopen("H.in", "r", stdin);
while(~scanf("%d", &N))
{
memset(len, 0, sizeof(len));
memset(nn, 0, sizeof(nn));
for(int i = 0; i < N; i++)
{
scanf("%d", &v[i]);
nn[0][i] = nn[1][N - i + 1] = Node(v[i], 0, 0, 0);
}
ans[0] = ans[1] = 0;
for(int i = 0; i < 2; i++) solve(nn[i], i);
printf("%I64d\n", min(ans[0], ans[1]));
}
return 0;
}