本节内容:
1:如何创建简单线性回归、多项式回归、多元线性回归、有显著交互项的多元线性回归
2:对回归的一些提前工作和回归后的操作
3:回归诊断-》summary没办法告诉你模型是否合适
4:多重共线性-》变量跟变量之间是否具有很强关系
5:异常点观测-离群点、高杠杆值点、强影响点
6:发现了以上问题如何改进
7:深层次的分析-泛化能力和变量相对重要性
一、如何创建简单线性回归、多项式回归、多元线性回归
简单线性回归:##采用R自带的women数据集,分析体重和更改的关系
fit1 = lm(weight~height,data=women) summary(fit)
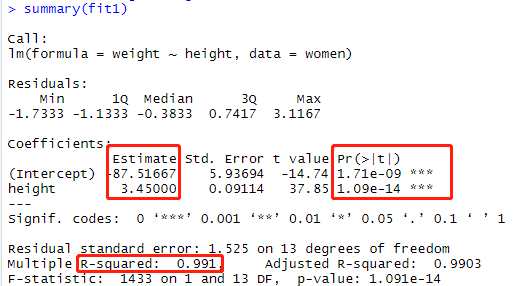
参数解释:
R方模型的整体评价是怎么样的,R方(0.991)可以解释99.1%的因变量Weight的值。 Estimate 参数的截距项和系数 Pr(>|t|)系数是否显著 H0:t检验所以是为0的原假设
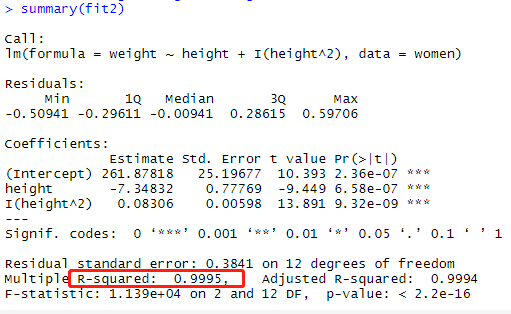
多项式回归:多项式回归其实也是单个的自变量对因变量的解释,只不过对自变量做了算数如对身高^2的算数
fit2= lm(weight~height+I(height^2),data=women) summary(fit2)
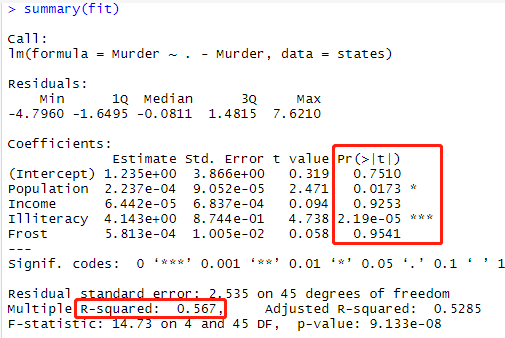
多元线性回归:##采用R自带的state.x77,关于每个谋杀率的数据集
states=as.data.frame(state.x77[,c("Population","Income","
Illiteracy","Frost","Murder")])
fit = lm(Murder~.-Murder,data=states)
summary(fit)
交互项的多元线性回归 ##采用R自带的mtcars数据集每加仑油与马力和车重的关系
fit = lm(mpg~hp+wt+hp:wt,data=mtcars) summary(fit)

对其中做图形:
library(effect)
fit = lm(mpg~hp+wt+hp:wt,data=mtcars)
summary(fit)
plot(effects("hp:wt",fit,list(wt=c(2.2,3.2,4.2))),multiline=True)
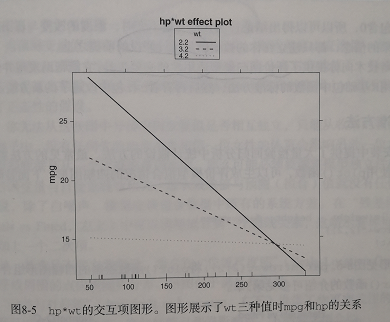
wt=c(2.2,3,2,4,2) 3.2是wt的均值 2.2和4.2是wt的一个标准差 可以看出随着车重的增加,马力和每加仑汽车行驶的英里数的关系减弱了,当wt=4.2的时候,直线几乎是水平的,表明随着hp的增加,mpg不会发生改变。
二、对回归前后的工作
在多元回归中,第一步最好先检查相关性:
①cor()
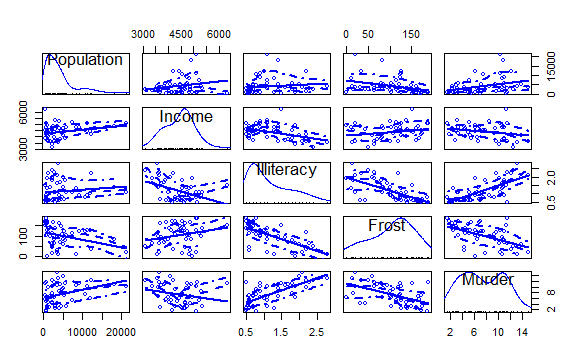
②car包的scatterplotMatrix()函数则会生成散点图矩阵
这个函数默认在非对角线区绘制变量间的散点图,并添加平滑和线性拟合曲线
states=as.data.frame(state.x77[,c("Population","Income",
"Illiteracy","Frost","Murder")])
library(car)
scatterplotMatrix(states)
③corrgram包的corrgram相关系数矩阵
library(corrgram)##要使用corrgram 需要安装mvtnorm,kernlab
library(mvtnorm)
library(kernlab)
states = as.data.frame(state.x77[,c("Population","Income",
"Illiteracy","Frost","Murder")])
corrgram(states,order = TRUE,lower.panel = panel.shade,
upper.panel = panel.pie,
text.panel = panel.txt,
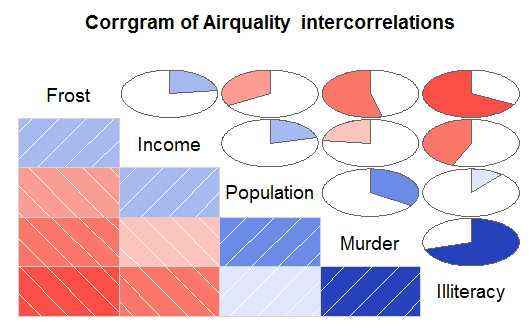
通过以上分析,谋杀率随着人口和文盲率的增加而增加,随着收入水平和结霜天数的增加而降低
三、回归诊断
标准办法:对回归模型做散点图
fit2 = lm(weight~height,data = women) par(mfrow=c(2,2)) plot(fit2)
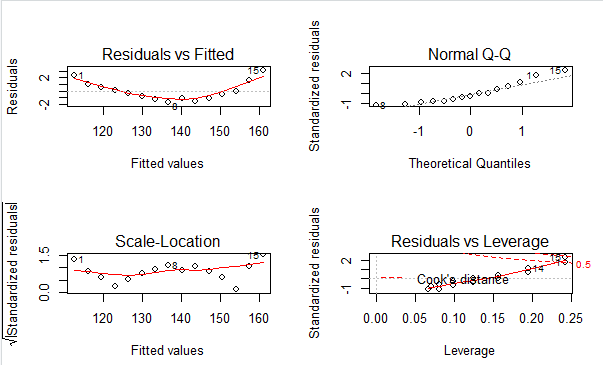
图解释:
①Normal-Q-Q(标准化残差图概率图) 解释了OLS回归统计假设的正态性-》 若满足正态假设,那么图上的点应该落在呈45°角的直线上,若不是,那么就违反了正态性假设 其他的OLS回归假设: ②Residuals vs Fitted(残差与预测拟合值)解释了OLS回归假设的线性-》 若因变量和自变量线性相关,那么残差与预测拟合值就没有任何关联。可是图可以看见 呈曲线关系,这暗示你需要对回归模型加一个二次项,也就是身高^2 ③Scale-Location(位置尺度图)解释了OLS回归假设的同方差性-》 若满足不变方差假设,那么在图中应该是随机分布的,此图似乎满足此假设 ④Residuals vs Leverage(残差与杠杆图)提供了单个观测点的信息-》 图中可以鉴别出离群点、高杠杆值点、强影响点 其他OLS假设: 独立性:没有任何先验的理由去相信一位女性的体重会影响另外一位女性的身高。
改进办法:car包的大量函数
正态性:qqPlot
library(car)
states = as.data.frame(state.x77[,c("Population","Income",
"Illiteracy","Frost","Murder")])
fit = lm(Murder~.-Murder,data=states)
qqPlot(fit,labels=row.names(states),id.method="identify",
simulate = TRUE,main="Q-Q Plot")
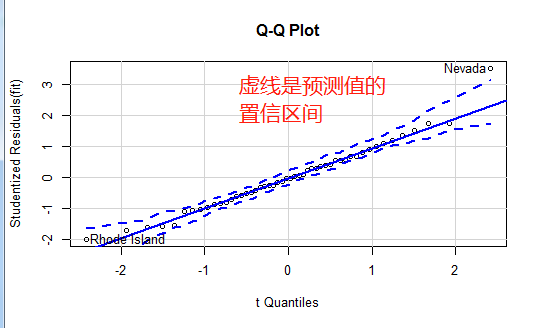
可以看出Nevada离线很远我们看下他的预测值和实际值
states["Nevada",] # Population Income Illiteracy Frost Murder #Nevada 590 5149 0.5 188 11.5 fitted(fit)["Nevada"] #Nevada #3.878958 residuals(fit)["Nevada"] # Nevada #7.621042 rstudent(fit)["Nevada"] #做标准化残差,我们说在正负2标准差我们任务是离群点看,Ne这个点的标准化残差值 #可以看到Nevada的谋杀率是11.5%,而预测值是3.9%
独立性:durbinWatsonTest():误差独立性 H0:独立
library(car)
states = as.data.frame(state.x77[,c("Population","Income",
"Illiteracy","Frost","Murder")])
fit = lm(Murder~.-Murder,data=states)
durbinWatsonTest(fit)

p值不显著(p=0.24)说明无自相关性,误差项之间独立。
线性:crPlots():(成分残差图)-》看看因变量和自变量是否呈现非线性关系
library(car) crPlots(fit)

从图中可以看出,成分残差图证实了线性假设,线性模型形式对该数据看似是合适的。
同方差性:
ncvTest(fit)-》判断误差方差是否恒定 H0:误差方差不变
spreadLevelPlot(fit)-》创建了一个最佳拟合曲线的散点图
> ncvTest(fit) Non-constant Variance Score Test Variance formula: ~ fitted.values Chisquare = 1.746514, Df = 1, p = 0.18632 ##p值不显著,说明满足方差不变假设
> spreadLevelPlot(fit) Suggested power transformation: 1.209626 ##Suggested是建议你将回归中的y进行y的p次幂转换 ##如何建议为0.5则表示你可以用y的平均根代替y,提高模型拟合
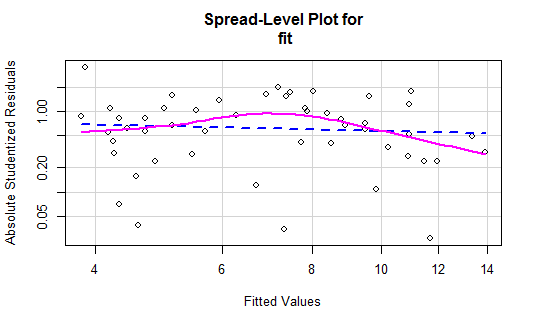
大招:直接判断模拟所有统计假设是不是可以
> library(gvlma) > gvmodel = gvlma(fit) > summary(gvmodel) ##gvlma包
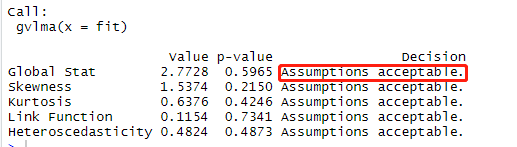
p值Global Stat(p=0.596)>0.05模型的假设检验通过。如果是小于0.05那么你就需要通过上面的办法去检验
到底哪个假设检验没通过。
四、多重共线性-》变量跟变量之间是否具有很强关系
采用VIF(variance Inflation Factor ,方差膨胀因子),当sqrt(vif)>2时就表明存在多重同线性

五、异常观测值
1:离群点 :car包outlierTest、car包中的qqPlot、学生残差图(rsrudent)
2:高杠杆值点 :帽子统计量(hat statistic)
3:强影响点 :cook距离与car包的avPlots()
4:一张图判断以上三种 :car包
1:离群点
前面我们已经学了一种鉴别的离群点的办法,可通过car包中的qqPlot落在置信区间外的可认为是离群点;
第二种我们通过rstudent(标准化学生残差)大于2或者小于-2的可能是离群点;
第三种我们通过car包outlierTest离群点统计检验方法,H0:是离群点
library(car)
states = as.data.frame(state.x77[,c("Population","Income",
"Illiteracy","Frost","Murder")])
fit = lm(Murder~.-Murder,data=states)
outlierTest(fit)

2:高杠杆值点
高杠杆值观测点,即与其他预测变量有关的离群点。换句话说,他们是由许多异常的预测变量值组合起来的,与响应变量没有关系。
方法:帽子统计量(hat statistic)判断。
hat.plot<-function(fit){
p<-length(coefficients(fit))
##参数数目,包含截距项
n<-length(fitted(fit))
##样本量
plot(hatvalues(fit),main="Index Plot of Hat Values")
abline(h=c(2,3)*p/n,col="red",lty=2)
##若观测点的帽子大于帽子均值的2倍或3倍,就认为是高杠杆值点
identify(1:n,hatvalues(fit),names(hatvalues(fit)))
}
hat.plot(fit)
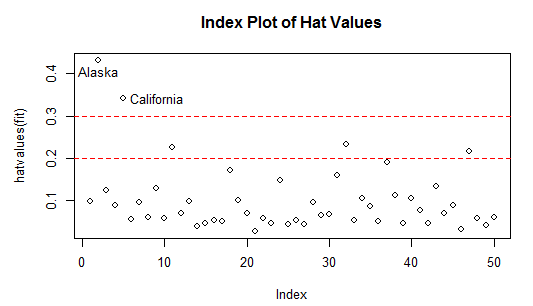
可以看到Alaska和California非常异常。高杠杆值点可能是强影响点也可能不是,要看他们是不是离群点。
3:强影响点
第一种:Cook距离
第二种:变量添加图
第一种:Cook距离
一般来说,Cook'D值大于4/(n-k-1),则表示它是强影响点
cutof = 4/(nrow(states) -length(fit$coefficients)-2) plot(fit,which=4,cook.levels = cutof) abline(h=cutof,lty=2,col="red")
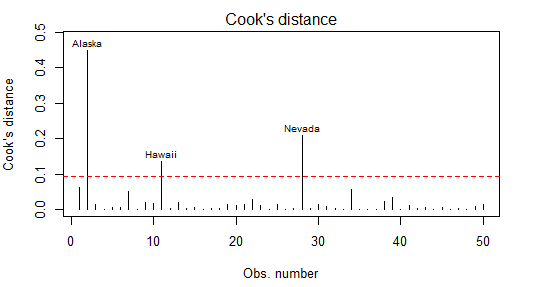
第二种:变量添加图
car包的avPlots()函数可提高变量添加图,图形一次生成一个,用户可以通过点击点来判断强影响点。
avPlots(fit,ask=FALSE,id.method="identify")

4:一张图判断以上三种
利用car包的influencePlot函数将离群点、高杠杆值点、强影响点整一张图
influencePlot(fit,id.method="identify",main="Influence Plot",
sub="Cricle size is proportional to Cook's distance")

影响图:纵坐标超过2或小于-2认为是离群点,水平轴超过0.2或0.3可能是高杠杆值点,
圆圈大小于影响成正比,圆圈越大可能是强影响点。
六、发现了以上问题如何改进
■删除观测点 (是否删除要持严谨的态度)
■变量替换
■添加或删除变量(常见的就是对存在多重共线性进行删除变量)
■使用其他回归方法 (模型比较、变量选择)
2:变量替换
(当模型不满足正态性、线性、或者同方差性假设时,一个或者多个变量变换可以改善或者调整模型结果)
常见的变换:
4:使用其他回归方法
模型的比较:
anova()函数可以比较两个嵌套函数的拟合优度
AIC(Akaile Information Criterion ,赤池信息准则) AIC值较小的模型要优先选择
states = as.data.frame(state.x77[,c("Population","Income",
"Illiteracy","Frost","Murder")])
fit1 = lm(Murder~Population+Income+Frost+Illiteracy,data=states)
fit2 = lm(Murder~Population+Illiteracy,data=states)
anova(fit1,fit2)
AIC(fit1,fit2)
#此处模型1嵌套模型2中,anova函数对是否要添加Income+Fros做了检验其p值#(0.994)不显著,H0:不放模型

变量选择
①逐步回归
library(MASS) stepAIC(fit,direction = "backward")
②全子集回归
library(leaps)
states = as.data.frame(state.x77[,c("Population","Income",
"Illiteracy","Frost","Murder")])
leaps=regsubsets(Murder~Population+Income+Frost+Illiteracy,
data=states,nbest=4)
plot(leaps,scale="adjr2") ##leaps做全子集图
library(car)
subsets(leaps,statistic="cp",main="Cp plot fot All Subsets Regression")
abline(1,1,lty=2,col="red") ##car做全子集图
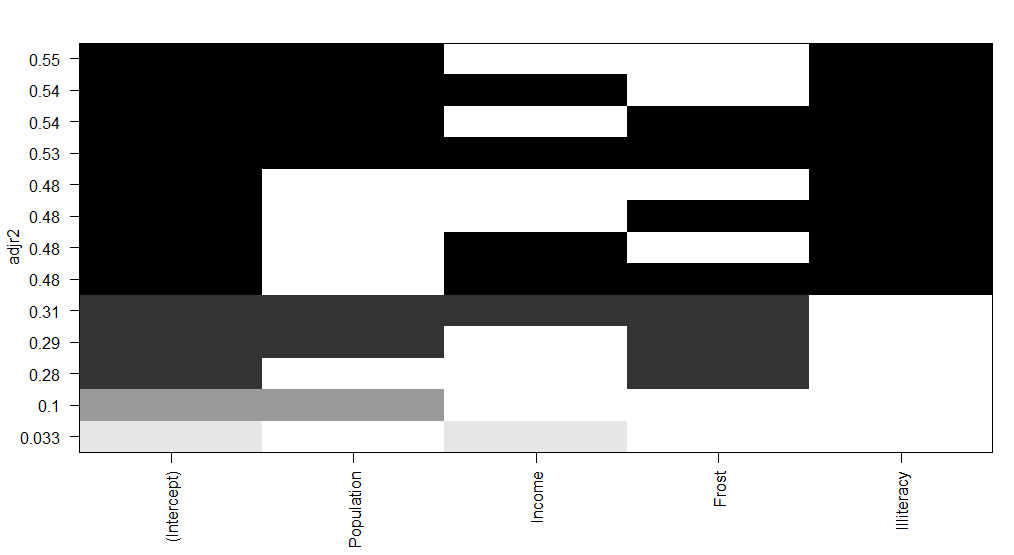
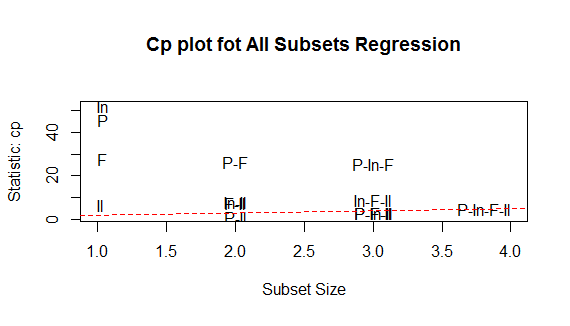
图1解读:水平轴为预测变量,纵坐标为调整R方, 当只有截距和income时R方是0.033 当只有截距、人口、文盲率R方达到了0.55 图2解读:越好的模型离截距项和斜率均为1的直线越进: 图形表明:你可以选择这个几种模型,其余的都不需要考虑 选择模型有:人口和文盲率双变量、人口与文盲率与冰冻三变量模型等
七、深层次的分析
模型的泛化能力和变量相对重要性方法
泛化能力:模型对新数据表现如何就叫做模型泛化能力,方法交叉验证:
所谓的交叉验证,将数据分为训练数据和测试数据,先训练数据做回归,再保留样本做预测。
栗子:
创建函数:shrinkage可获得初始R方和交叉验证后的R方
shrinkage= function(fit,k=10){
require(bootstrap)
theta.fit =function(x,y){lsfit(x,y)}
theta.predict = function(fit,x){cbind(1,x)%*%fit$coef}
x = fit$model[,2:ncol(fit$model)]
y = fit$model[,1]
results = crossval(x,y,theta.fit,theta.predict,ngroup = k)
r2 = cor(y,fit$fitted.values)^2
r2cv = cor(y,results$cv.fit)^2
cat("Original R-square=",r2,"
")
cat(k,"Fold cross-Validated R-square=",r2cv,"
")
cat("change=",r2-r2cv,"
")
}
states = as.data.frame(state.x77[,c("Population","Income","Illiteracy","Frost","Murder")])
fit = lm(Murder~.-Murder,data=states)
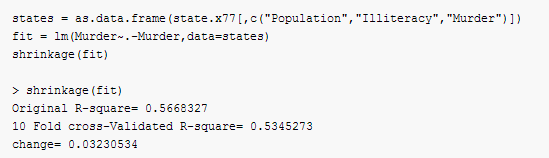
shrinkage(fit)

可以看到,基于初始样本R方(0.567)过于乐观了,对新数据更好的方差解释率估计是交叉验证后的R方(0.484)
这里,我们可以选择模型变量是4个,我们可以选择具有更好的泛化能力的模型,比如说我们值采用两个变量
变量的相对性
我们一直会存在一个疑问“哪些变量对预测变量有用呢?”又或者是“哪些变量对预测最为重要”
如果预测变量之间不相关,我们直接采用相关系数就可以了,但是大部分情况预测变量之间具有一定的关系。
如此我们去分析变量的相对性就比较复杂了:我们通过以下两种办法
①将数据标准化,然后采用coef函数对回归模型做分析
states = as.data.frame(state.x77[,c("Population","Illiteracy",
"Murder","Income","Frost")])
zstates = as.data.frame(scale(states))
fit = lm(Murder~.-Murder,data=zstates)
coef(fit)
> coef(fit)
(Intercept) Population Illiteracy Income Frost
-2.054026e-16 2.705095e-01 6.840496e-01 1.072372e-02 8.185407e-03
此处可以看到,当其他因数不变时,文盲率一个标准差的变化将增加0.68个标准差的谋杀率。
根据这个我们认为Frost最不重要
②相对权重:在整体的R方解释量时,各个变量对其解释的程度
构建:分析相对权重函数relweghts
relweghts <- function(fit,...){
R <-cor(fit$model)
nvar <-ncol(R)
rxx <-R[2:nvar,2:nvar]
rxy<-R[2:nvar,1]
svd<-eigen(rxx)
evec<-svd$vectors
ev<-svd$values
delta<-diag(sqrt(ev))
lambda<-evec %*% delta %*% t(evec)
lambdasq<-lambda^2
beta<-solve(lambda)%*%rxy
rsquare<-colSums(beta^2)
rawwgt<-lambdasq %*% beta^2
import<-(rawwgt/rsquare)*100
import<-as.data.frame(import)
row.names(import)<-names(fit$model[2:nvar])
names(import)<-"Weights"
import<-import[order(import),1,drop=FALSE]
dotchart(import$Weights,labels = row.names(import),
xlab="% of R-Square",pch=19,
main="Relative Impotance of Predictor Variables",
sub=paste("Total R-Square=",round(rsquare,digits = 3)),...)
return(import)
}
代码清单:
states = as.data.frame(state.x77[,c("Population","Illiteracy",
"Murder","Income","Frost")])
fit = lm(Murder~.-Murder,data=states)
relweghts(fit,col="blue")
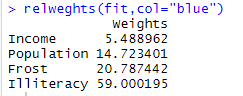
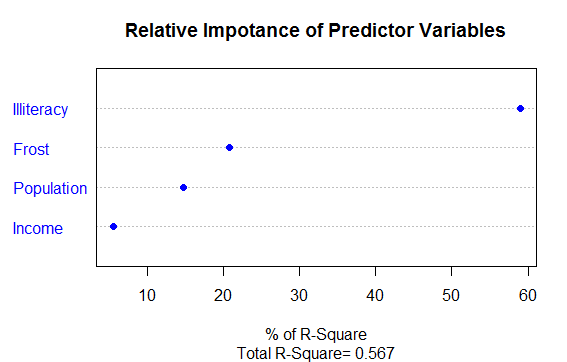
通过图形:我们整体R方是(0.567)Illiteracy解释了59%的R方,Frost解释了20.79%,根据相对权重的重要性分别是:
"Illiteracy","Frost"Population","Income",