标准二维表问题

问题描述：

设n 是一个正整数。2xn的标准2维表是由正整数1，2，…，2n 组成的2xn 数组，该数组的每行从左到右递增，每列从上到下递增。2xn的标准2维表全体记为Tab(n)。

例如，当n=3时Tab(3)如下：

思路分析：首先明确一下每行的数总是左边小于后面，上面小于下面，以上面的第一种情况进行分析，我们把第一行的数字对应为1表示进栈

。第二行的数字对应为-1表示出栈。我们知道一般情况进栈和出栈时栈里面的元素个数大于等于0，那么数字1看成进栈-1看成出栈，则总数之和要大于等于0。

即进出栈操作任何时刻进栈次数大于等于出栈的次数。那么上表的第一行第一个元素表示第一次是进栈操作，下面的4对应的是第一次进栈的元素在第四次出栈，第一行第二列2

表示第二次操作是进栈对应对应下面的5表示第五次操作是出栈，即把第二次进栈操作的元素出栈，依次类推，第三次是进栈操作，第六次把第三次进栈的元素弹出栈。

所以我们可以把表看出是元素的进出栈的操作，则tab(n)表示求元素个数为n的所有可能进出栈的操作。于是问题转换为n个元素所有可能进出栈的情况。

而求进出栈的所有可能情况的方法就是卡特兰数。下面简单介绍一下卡特兰数。

事实上，可以认为问题是，任意两种操作，要求每种操作的总次数一样，且进行第k次操作2前必须先进行至少k次操作1。我们假设一个人在原点，操作1是此人沿右上角45°走一个单位（一个单位设为根号2，这样他第一次进行操作1就刚好走到（1,1）点），操作2是此人沿右下角45°走一个单位。第k次操作2前必须先进行至少k次操作1，就是说明所走出来的折线不能跨越x轴走到y=-1这条线上！在进行n次操作1和n此操作2后，此人必将到到达（2n，0）！若无跨越x轴的限制，折线的种数将为C（2n，n），即在2n次操作中选出n次作为操作1的方法数。

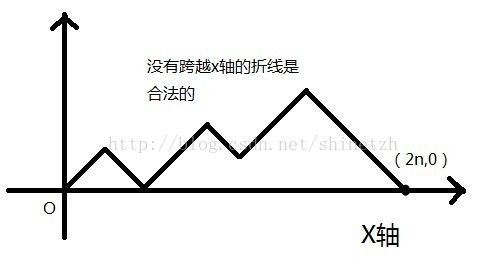
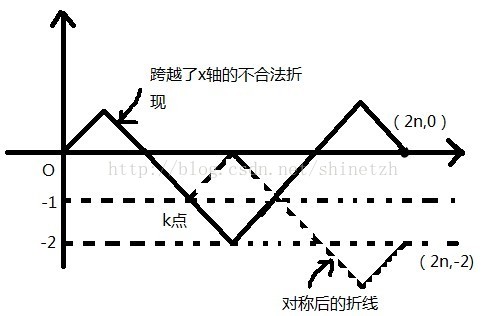
现在只要减去跨越了x轴的情况数。对于任意跨越x轴的情况，必有将与y=-1相交。找出第一个与y=-1相交的点k，将k点以右的折线根据y=-1对称（即操作1与操作2互换了）。可以发现终点最终都会从（2n，0）对称到（2n，-2）。由于对称总是能进行的，且是可逆的。我们可以得出所有跨越了x轴的折线总数是与从（0,0）到（2n,-2）的折线总数。而后者的操作2比操作1要多0-（-2）=2次。即操作1为n-1,操作2为n+1。总数为C（2n，n-1）。

catalan数和出栈序列的对应：

动态规划：我们把n个元素的出栈个数的记为f(n), 那么对于1,2,3, 我们很容易得出：

f(1) = 1 //即 1

f(2) = 2 //即 12、21

f(3) = 5 //即 123、132、213、321、231

然后我们来考虑f(4), 我们给4个元素编号为a,b,c,d, 那么考虑：元素a只可能出现在1号位置，2号位置，3号位置和4号位置(很容易理解，一共就4个位置，比如abcd,元素a就在1号位置)。

分析：

1) 如果元素a在1号位置，那么只可能a进栈，马上出栈，此时还剩元素b、c、d等待操作，就是子问题f(3)；

2) 如果元素a在2号位置，那么一定有一个元素比a先出栈，即有f(1)种可能顺序（只能是b），还剩c、d，即f(2)，根据乘法原理，一共的顺序个数为f(1) * f(2)；

3) 如果元素a在3号位置，那么一定有两个元素比1先出栈，即有f(2)种可能顺序（只能是b、c），还剩d，即f(1)，

根据乘法原理，一共的顺序个数为f(2) * f(1)；

4) 如果元素a在4号位置，那么一定是a先进栈，最后出栈，那么元素b、c、d的出栈顺序即是此小问题的解，即 f(3)；

结合所有情况，即f(4) = f(3) + f(2) * f(1) + f(1) * f(2) + f(3);

为了规整化，我们定义f(0) = 1；于是f(4)可以重新写为：

f(4) = f(0)*f(3) + f(1)*f(2) + f(2) * f(1) + f(3)*f(0)

然后我们推广到n，推广思路和n=4时完全一样，于是我们可以得到：

f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... + f(n-1)*f(0)

下面是推导式，不给证明了

另类递推式:

h(n)=h(n-1)*(4*n-2)/(n+1);

递推关系的解为:

h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

递推关系的另类解为:

h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)

那么我们了解了卡特兰数之后就可以写代码了，demo如下

 1 #include<bits/stdc++.h>
 2 
 3 using namespace std;
 4 int tan(int n){
 5 if(n==1|| n==0)
 6 return 1;
 7 else if(n==2)
 8 return 2;
 9 else {
10 return tan(n-1)*(4*n-2)/(n+1);
11 }
12 
13 }
14 int main()
15 {
16 int n;
17 cin >> n;
18 cout << tan(n);
19 return 0;
20 }

但是这个代码只是简单运用了卡特兰数解决了n较小的问题，但是如下

其前几项为 : 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...

所以n较大的时候Int就无法表示，下面是处理大整数后的思路（关于大整数的内容可以我的参考这篇博客（https://www.cnblogs.com/henuliulei/p/9867127.html））

下面是具体的大卡特兰数

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 char array1[200];
  4 char array2[200];
  5 int sum[400];
  6 string f(string s1,string s2)//大整数乘法
  7 {
  8 reverse(s1.begin(),s1.end());
  9 reverse(s2.begin(),s2.end());
 10 memset(array1,0,sizeof(s1));
 11 memset(array2,0,sizeof(s2));
 12 memset(sum,0,sizeof(sum));
 13 int l1=s1.length();
 14 int l2=s2.length();
 15 strcpy(array1,s1.c_str());
 16 strcpy(array2,s2.c_str());
 17 for(int i=0;i<l1;i++){
 18 for(int j=0;j<l2;j++){
 19 sum[i+j]+=((int)array1[i]-48)*((int)array2[j]-48);
 20 }
 21 }
 22 int f=0;
 23 while(true){
 24 
 25 if(f<l1+l2){
 26 int de=sum[f]/10;
 27 sum[f]=sum[f]%10;
 28 sum[f+1]+=de;
 29 f++;
 30 }
 31 else{
 32 break;
 33 }
 34 }
 35 string a="";
 36 int ig=0;
 37 for(int i=l1+l2-1;i>=0;i--){
 38 if((char)sum[i]+48!='0'){
 39 ig=1;
 40 }
 41 if(ig==1){
 42 a+=(char)sum[i]+48;
 43 }
 44 }
 45 return a;
 46 }
 47 string div(string a,int b){//大整数除法
 48 
 49 char s[1000];
 50 memset(s,0,sizeof(s));
 51 unsigned long long sum=0;
 52 for(int i=0;a[i];i++)
 53 {
 54 sum=sum*10+a[i]-'0';
 55 s[i]=sum/b+'0';
 56 sum=sum%b;
 57 }
 58 int j=0;
 59 string as="";
 60 while(s[j]=='0')
 61 j++;
 62 
 63 for(;j<a.size();j++)
 64 as+=s[j];//商
 65 return as;
 66 
 67 }
 68 int t(string n)//把字符串变为int类型
 69 {
 70 int a=0;
 71 int s=1;
 72 for(int i=n.length()-1;i>=0;i--){
 73 a+=((int)n[i]-48)*(s);
 74 s*=10;
 75 }
 76 return a;
 77 }
 78 string tan(string n){//递归实现卡特兰数
 79 if(n=="1"|| n=="0")
 80 return "1";
 81 else if(n=="2")
 82 return "2";
 83 else {
 84 int s=t(n);
 85 s=(s+1);
 86 int st=t(n)*4-2;
 87 int s1=t(n);
 88 s1--;
 89 char a[100];
 90 char a1[100];
 91 itoa(st,a,10);
 92 itoa(s1,a1,10);
 93 string s2=tan(a1);
 94 string re=div(f(s2,a),s);
 95 return re;
 96 }
 97 }
 98 int main()
 99 {
100 string s1;
101 string s2;
102 string s3;
103 cin >> s1;
104 cout << tan(s1);
105 }