DBSCAN,英文全写为Density-based spatial clustering of applications with noise ,是在 1996 年由Martin Ester, Hans-Peter Kriegel, Jörg Sander 及 Xiaowei Xu 提出的聚类分析算法, 这个算法是以密度为本的:给定某空间里的一个点集合,这算法能把附近的点分成一组(有很多相邻点的点),并标记出位于低密度区域的局外点(最接近它的点也十分远),DBSCAN 是其中一个最常用的聚类分析算法,也是其中一个科学文章中最常引用的。
在 2014 年,这个算法在领头数据挖掘会议 KDD 上获颁发了 Test of Time award,该奖项是颁发给一些于理论及实际层面均获得持续性的关注的算法。
目录
- 1基础知识
- 2算法
- 3复杂度
- 4优点
- 5缺点
- 6有关文章
- 7注意
- 8参考文献
- 8.1延伸阅读
基础知识
考虑在某空间里将被聚类的点集合,为了进行 DBSCAN 聚类,所有的点被分为核心点,(密度)可达点及局外点,详请如下:
- 如果一个点 p 在距离 ε 范围内有至少 minPts 个点(包括自己),则这个点被称为核心点,那些 ε 范围内的则被称为由 p 直接可达的。同时定义,没有任何点是由非核心点直接可达的。
- 如果存在一条道路 p1, ..., pn ,有 p1 = p和pn = q, 且每个 pi+1 都是由 pi 直接可达的(道路上除了 q 以外所有点都一定是核心点),则称 q 是由 p 可达的。
- 所有不由任何点可达的点都被称为局外点。
如果 p 是核心点,则它与所有由它可达的点(包括核心点和非核心点)形成一个聚类,每个聚类拥有最少一个核心点,非核心点也可以是聚类的一部分,但它是在聚类的“边缘”位置,因为它不能达至更多的点。
“可达性”(英文:Reachability )不是一个对称关系,因为根据定义,没有点是由非核心点可达的,但非核心点可以是由其他点可达的。所以为了正式地界定 DBSCAN 找出的聚类,进一步定义两点之间的“连结性”(英文:Connectedness) :如果存在一个点 o 使得点 p 和点 q 都是由 o 可达的,则点 p 和点 q 被称为(密度)连结的,而连结性是一个对称关系。
定义了连结性之后,每个聚类都符合两个性质:
- 一个聚类里的每两个点都是互相连结的;
- 如果一个点 p 是由一个在聚类里的点 q 可达的,那么 p 也在 q 所属的聚类里。
算法
DBSCAN 需要两个参数:ε (eps) 和形成高密度区域所需要的最少点数 (minPts),它由一个任意未被访问的点开始,然后探索这个点的 ε-邻域,如果 ε-邻域里有足够的点,则建立一个新的聚类,否则这个点被标签为杂音。注意这个点之后可能被发现在其它点的 ε-邻域里,而该 ε-邻域可能有足够的点,届时这个点会被加入该聚类中。
如果一个点位于一个聚类的密集区域里,它的 ε-邻域里的点也属于该聚类,当这些新的点被加进聚类后,如果它(们)也在密集区域里,它(们)的 ε-邻域里的点也会被加进聚类里。这个过程将一直重复,直至不能再加进更多的点为止,这样,一个密度连结的聚类被完整地找出来。然后,一个未曾被访问的点将被探索,从而发现一个新的聚类或杂音。
算法可以以下伪代码表达,当中变数根据原本刊登时的命名:
DBSCAN(DB, dist, eps, minPts) {
C = 0 /* Cluster counter */
for each point P in database DB {
if label(P) ≠ undefined then continue /* Previously processed in inner loop */
Neighbors N = RangeQuery(DB, dist, P, eps) /* Find neighbors */
if |N| < minPts then { /* Density check */
label(P) = Noise /* Label as Noise */
continue
}
C = C + 1 /* next cluster label */
label(P) = C /* Label initial point */
Seed set S = N {P} /* Neighbors to expand */
for each point Q in S { /* Process every seed point */
if label(Q) = Noise then label(Q) = C /* Change Noise to border point */
if label(Q) ≠ undefined then continue /* Previously processed */
label(Q) = C /* Label neighbor */
Neighbors N = RangeQuery(DB, dist, Q, eps) /* Find neighbors */
if |N| ≥ minPts then { /* Density check */
S = S ∪ N /* Add new neighbors to seed set */
}
}
}
}
where RangeQuery can be implemented using a database index for better performance, or using a slow linear scan:
RangeQuery(DB, dist, Q, eps) {
Neighbors = empty list
for each point P in database DB { /* Scan all points in the database */
if dist(Q, P) ≤ eps then { /* Compute distance and check epsilon */
Neighbors = Neighbors ∪ {P} /* Add to result */
}
}
return Neighbors
}
注意这个算法可以以下方式简化:其一,"has been visited" 和 "belongs to cluster C" 可被结合起来,另外 "expandCluster" 副程式不必被抽出来,因为它只在一个位置被调用。以上算法没有以简化方式呈现,以反映原本出版的版本。另外,regionQuery 是否包含 P 并不重要,它等价于改变 MinPts 的值。
复杂度
DBSCAN 对数据库里的每一点进行访问,可能多于一次(例如作为不同聚类的候选者),但在现实的考虑中,时间复杂度主要受regionQuery 的调用次数影响,DBSCAN 对每点都进行刚好一次呼叫,且如果使用了特别的编号结构,则总平均时间复杂度为 O(n log n) ,最差时间复杂度则为 O(n^2) 。可以使用 O(n^2) 空间复杂度的距离矩阵以避免重复计算距离,但若不使用距离矩阵,DBSCAN 的空间复杂度为 O(n)。
优点
- 相比 k-平均,DBSCAN 不需要预先声明聚类数量。
- DBSCAN 可以找出任何形状的聚类,甚至能找出一个聚类,它包围但不连接另一个聚类,另外,由于 MinPts 参数,single-link effect (不同聚类以一点或极幼的线相连而被当成一个聚类)能有效地被避免。
- DBSCAN 能分辨噪音(局外点)。
- DBSCAN 只需两个参数,且对数据库内的点的次序几乎不敏感(两个聚类之间边缘的点有机会受次序的影响被分到不同的聚类,另外聚类的次序会受点的次序的影响)。
- DBSCAN 被设计成能配合可加速范围访问的数据库结构,例如 R*树。
- 如果对资料有足够的了解,可以选择适当的参数以获得最佳的分类。
缺点
- DBSCAN 不是完全决定性的:在两个聚类交界边缘的点会视乎它在数据库的次序决定加入哪个聚类,幸运地,这种情况并不常见,而且对整体的聚类结果影响不大——DBSCAN 对核心点和噪音都是决定性的。DBSCAN* 是一种变化了的算法,把交界点视为噪音,达到完全决定性的结果。
- DBSCAN 聚类分析的质素受函数 regionQuery(P,ε) 里所使用的度量影响,最常用的度量是欧几里得距离,尤其在高维度资料中,由于受所谓“维数灾难”影响,很难找出一个合适的 ε ,但事实上所有使用欧几里得距离的算法都受维数灾难影响。
- 如果数据库里的点有不同的密度,而该差异很大,DBSCAN 将不能提供一个好的聚类结果,因为不能选择一个适用于所有聚类的 minPts-ε 参数组合。
- 如果没有对资料和比例的足够理解,将很难选择适合的 ε 参数。
有关文章
- OPTICS algorithm: 一个DBSCAN的一般化,有效地以“最大搜寻半径”代替 ε 参数。
- Connected component
- 并查集
注意
参考文献
延伸阅读
- Arlia, Domenica; Coppola, Massimo. "Experiments in Parallel Clustering with DBSCAN". Euro-Par 2001: Parallel Processing: 7th International Euro-Par Conference Manchester, UK August 28–31, 2001, Proceedings. Springer Berlin.
- Kriegel, Hans-Peter; Kröger, Peer; Sander, Jörg; Zimek, Arthur (2011). "Density-based Clustering". WIREs Data Mining and Knowledge Discovery. 1 (3): 231–240. doi:10.1002/widm.30.
转载自维基百科,原文链接:https://zh.wikipedia.org/wiki/DBSCAN
参考2:
1.DBSCAN密度聚类简介
DBSCAN 算法是一种基于密度的聚类算法:
1.聚类的时候不需要预先指定簇的个数
2.最终的簇的个数不确定
DBSCAN算法将数据点分为三类:
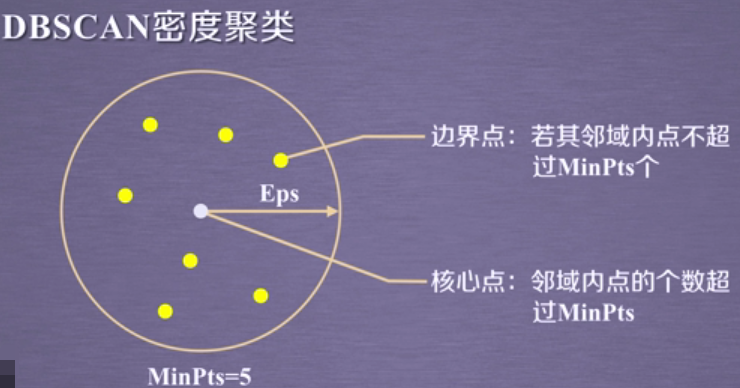
1.核心点:在半径Eps内含有超过MinPts数目的点。
2.边界点:在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内的点。
3.噪音点:既不是核心点也不是边界点的点。
如下图所示:图中黄色的点为边界点,因为在半径Eps内,它领域内的点不超过MinPts个,我们这里设置的MinPts为5;而中间白色的点之所以为核心点,是因为它邻域内的点是超过MinPts(5)个点的,它邻域内的点就是那些黄色的点!
2.DBSCAN算法的流程
1.将所有点标记为核心点、边界点或噪声点;(具体来说,先找到核心点,然后对未归类的点进行判断是边界点还是噪声点(判断是否位于核心点的领域内))。
2.删除噪声点;
3.为距离在Eps之内的所有核心点之间赋予一条边;
4.每组连通的核心点形成一个簇;
5.将每个边界点指派到一个与之关联的核心点的簇中(哪一个核心点的半径范围之内)。
原文链接:https://www.cnblogs.com/bonelee/p/8692336.html

