(L1)正则化及其推导
在机器学习的Loss函数中,通常会添加一些正则化(正则化与一些贝叶斯先验本质上是一致的,比如(L2)正则化与高斯先验是一致的、(L1)正则化与拉普拉斯先验是一致的等等,在这里就不展开讨论)来降低模型的结构风险,这样可以使降低模型复杂度、防止参数过大等。大部分的课本和博客都是直接给出了(L1)正则化的解释解或者几何说明来得到(L1)正则化会使参数稀疏化,本来会给出详细的推导。
(L1)正则化
大部分的正则化方法是在经验风险或者经验损失(L_{emp})(emprirical loss)上加上一个结构化风险,我们的结构化风险用参数范数惩罚(Omega( heta)),用来限制模型的学习能力、通过防止过拟合来提高泛化能力。所以总的损失函数(也叫目标函数)为:
其中(X)是输入数据,(y)是标签,( heta)是参数,(alpha in [0,+infty])是用来调整参数范数惩罚与经验损失的相对贡献的超参数,当(alpha = 0)时表示没有正则化,(alpha)越大对应该的正则化惩罚就越大。对于(L1)正则化,我们有:
其中(w)是模型的参数。
几何解释
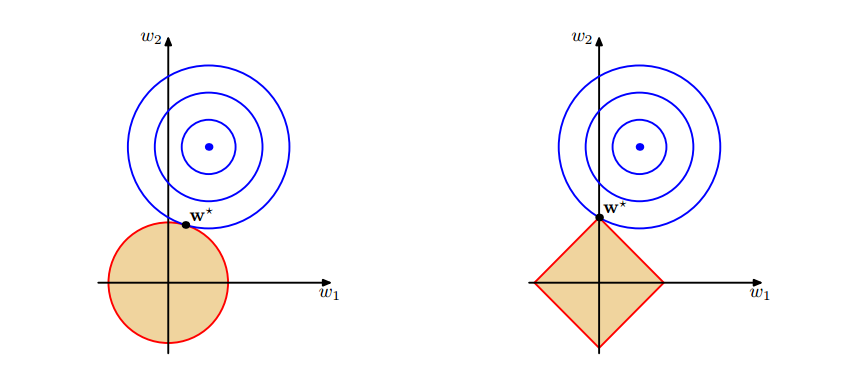
可以看到在正则化的限制之下,(L2)正则化给出的最优解(w^*)是使解更加靠近原点,也就是说(L2)正则化能降低参数范数的总和。(L1)正则化给出的最优解(w^*)是使解更加靠近某些轴,而其它的轴则为0,所以(L1)正则化能使得到的参数稀疏化。
解析解的推导
有没有偏置的条件下,( heta)就是(w),结合式((1.1))与((1.2)),我们可以得到(L1)正则化的目标函数:
我们的目的是求得使目标函数取最小值的(w^*),上式对(w)求导可得:
其中若(w>0),则(sign(w)=1);若(w<0),则(sign(w) = -1);若(w=0),则(sign(w)=0)。当(alpha = 0),假设我们得到最优的目标解是(w^*),用秦勤公式在(w^*)处展开可以得到(要注意的( abla J(w^*)=0)):
其中(H)是关于(w)的Hessian矩阵,为了得到更直观的解,我们简化(H),假设(H)这对角矩阵,则有:
将上式代入到式((3.1))中可以得到,我们简化后的目标函数可以写成这样:
从上式可以看出,(w)各个方向的导数是不相关的,所以可以分别独立求导并使之为0,可得:
我们先直接给出上式的解,再来看推导过程:
从式((3.5))与式((3.6))可以得到两点:
- 1.可以看到式((3.5))中的二次函数是关于(w^*)对称的,所以若要使式((3.5))最小,那么必有:(|w_i|<|w^*|),因为在二次函数值不变的程序下,这样可以使得(alpha|w_i|)更小。
- 2.(sign(w_i)=sign(w_i^*))或(w_1=0),因为在(alpha|w_i|)不变的情况下,(sign(w_i)=sign(w_i^*))或(w_i=0)可以使式((3.5))更小。
由式((3.6))与上述的第2点:(sign(w_i)=sign(w_i^*))可以得到:
我们再来看一下第2点:(sign(w_i)=sign(w_i^*))或(w_1=0),若(|w_i^*| < frac{alpha}{H_{i,i}}),那么有(sign(w_i)
eq sign(w_i^*)),所以这时有(w_1=0),由于可以直接得到解式((3.7))。
从这个解可以得到两个可能的结果:
- 1.若(|w_i^*| leq frac{alpha}{H_{i,i}}),正则化后目标中的(w_i)的最优解是(w_i=0)。因为这个方向上(L_{emp}(w; X, y))的影响被正则化的抵消了。
- 2.若(|w_i^*| > frac{alpha}{H_{i,i}}),正则化不会推最优解推向0,而是在这个方面上向原点移动了(frac{alpha}{H_{i,i}})的距离。
【防止爬虫转载而导致的格式问题——链接】:http://www.cnblogs.com/heguanyou/p/7582578.html