参考:
http://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/geometry/how-does-matrix-work-part-1
http://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/geometry/how-does-matrix-work-part-2
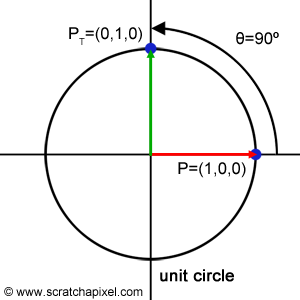
在scratchapixel的教程中,旋转矩阵是一种能将点或者向量绕某个轴旋转的矩阵,这里说的点和向量,是以自然基(或称为标准基)为基底的。
如上图,Z轴为贯穿屏幕的轴,点P绕Z轴逆时针旋转到Pt,记旋转矩阵为R,则三者的关系是:P • R = Pt
在scratchapixe的l教程中,作者最后试算出了这样的R,但并未做证明,这样的R,由旋转的轴不同,分别有绕X轴旋转的Rx,绕Y轴旋转的Ry,绕Z轴旋转的Rz:

其中Θ是逆时针旋转的角度
假设点P的坐标是(1,0,0),让它绕Z轴顺时针旋转Θ角(弧度单位),那么Pt的坐标是(cos(Θ), sin(Θ), 0),例如Θ是π/2时,Pt的坐标是(0, -1, 0)
假设点P的坐标是(0,1,0),让它绕Z轴顺时针旋转Θ角(弧度单位),那么Pt的坐标是(-sin(Θ), cos(Θ), 0),例如Θ是π/2时,Pt的坐标是(1, 0, 0)
刚好是分别是Rz的前两行,在scratchapixe的l教程中说,“理解矩阵Rz的关键一点,就是其每一行代表了坐标系中的一个轴,整个Rz代表了一组基”
这其实有点难以理解,于是翻出居余马的线性代数,第四章讲向量空间与线性变换,里面有关于基的定义是这样的:
定义:设有序向量组B={ß1, ß2…ßn}是实向量空间Rn的子集,如果B线性无关,则Rn中任一向量α,均可由B线性表示即
α = a1ß1 + a2ß2 + … + anßn
就称B是Rn这个实向量空间中的一组基(或基底),有序数组(a1, a2 … an)是向量α关于基B(或说在基B下)的坐标,记作αB = (a1, a2 … an) 或 αB = (a1, a2 … an) T
可以看到,scratchapixe阐述的角度是如何让一个点或者向量,乘以一个矩阵,移动到同一个坐标系的另外一个位置
而线性代数上,阐述的是同一个点在两组不同的基的坐标,以及两组基之间的过度矩阵怎样计算
而二者的内在联系具体怎样理解,我还要继续学习一下