步步为零

步步为零(dp (starstar))

你是否听说过这个游戏？游戏者在一张特殊的表格中按照规则跳动，使得跳到的数字经过加号和减号的连接，尽可能的逼近零。表格通常是如图 (1.1) 所示的形状，大小由中间一行的方格数 (N) 决定(图 (1.1) 就是一个 (N=4) 的例子)。
游戏者通常是从最下面的方格出发，按照如图 (1.2) 所示的规则在表格中跳动，当游戏者跳到最顶端的方格时，游戏结束。在游戏未结束前，游戏者不允许跳到表格外。
将游戏者跳到的 (2*N-1)个数字依次写下来，在每两个相邻的数字中间加上加号或减号，使得计算结果最接近零。
例如对于图 (1.1) 所示的表格，最好的跳动及计算方案是：(7+8+(-5)+(-2)-5-1-2=0) 或 (7+10+(-7)-6+(-3)-3+2=0) 或 (7+10+(-5)-10-5+1+2=0) 或 (7+10+(-5)+(-2)-5-3-2=0)。

Input

输入文件的第一行是 (N(N<=50)) ，接下来 (2*N-1) 行给出了表格中每行的每个方格中的数字，第 (i+1) 行的第 (j) 个数字对应于表格中第 (i) 行的第 (j) 个数字。
文件中第二行的数字表示的是表格顶端的方格中的数字。文件中所有的数字都是整数，同一行相邻的两个数字间用空格符隔开。

Output

输出文件只有一行，是你所求出的最接近零的计算结果的绝对值。

Sample Input

Sample Output

Hint

表格中的所有数字大于等于(-50)，小于等于(50)。
来源：

分析

这道题的大致意思是：在一个特殊的表格中求一条路线，使得路线上的数字经过加减运算结果最逼近(0)。
对于表格中的每一个数字要记录以这个数字为结尾的算式可以有哪几种结果。例如，对于下面的数据：
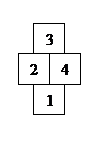
我们要想知道从(1)到 (3) 的跳动方案中计算结果的绝对值最小的，就等价于求从 (1) 到 (3) 的跳动方案可以计算出的每一种结果，然后从中选取绝对值最小的输出。
而从(1)到(3)的每一种结果都是通过从 (1) 到 (2)或者从 (1) 到 (4) 的所有计算结果加上或减去 (3) 得到的，所以要想求从(1)到 (3) 的跳动方案的所有可能的结果，就要先求从 (1) 到 (2) 和 (4) 的跳动方案的所有可能的结果。
考虑到 (N) 最大为 (30)，如果保存从底端方格到表格中每个方格的所有可能的结果，需要的空间为(30*30*6000/1024=5274KB)。但是从底端方格到顶端方格的跳动方案只依赖于从底端方格到第二行的所有方格的跳动方案；这样用滚动数组可以压一维 (2*30*6000/1024=351KB)。

Code

#include <bits/stdc++.h>
using namespace std;
const int maxn=30+5,Inf=0x3f3f3f3f;
int a[maxn<<1][maxn],n,tot;
bool dp[maxn<<1][maxn][6005];//dp[i][j][k]:从2*n-1行到第i行j列时，之前是否能组成k
bool Judge(int x){
    if(x<0 || x>2*tot)return 0;
    return 1;
}
void Init(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i){//上半个
        int Max=0;//求出每行的最大值
        for(int j=1;j<=i;++j){
            scanf("%d",&a[i][j]);
            a[i][j]=abs(a[i][j]);//全变成正数好处理
            Max=std::max(Max,a[i][j]);
        }
        tot+=Max;
    }
    for(int i=1;i<n;++i){//下半个
        int Max=0;
        for(int j=1;j<=n-i;++j){
            scanf("%d",&a[n+i][j]);
            a[n+i][j]=abs(a[n+i][j]);
            Max=std::max(Max,a[n+i][j]);
        }
        tot+=Max;
    }
}
void Solve(){
    dp[2*n-1][1][tot]=1;//为避免负数，整体往上平移tot，此时tot相当于0
    int now=0;
    for(int i=2*n-1;i>n;--i)//枚举下面的n-1行
        for(int j=1;j<=2*n-i;++j)//第j列
            for(int k=0;k<=2*tot;++k){//组成0~2*tot,实际上是-tot~tot
                if(dp[i][j][k]){//如果上一阶段值k为真
                    now=k+a[i][j];
                    if(Judge(now))
                        dp[i-1][j][now]=dp[i-1][j+1][now]=1;
                    now=k-a[i][j];
                    if(Judge(now))
                        dp[i-1][j][now]=dp[i-1][j+1][now]=1;
                }                
            }
    for(int i=n;i>=1;i--)//枚举上面的n行
        for(int j=1;j<=i;++j)
            for(int k=0;k<=2*tot;++k)
                if(dp[i][j][k]){
                    now=k+a[i][j];
                    if(Judge(now))
                        dp[i-1][j][now]=dp[i-1][j-1][now]=1;
                    now=k-a[i][j];
                    if(Judge(now))
                        dp[i-1][j][now]=dp[i-1][j-1][now]=1;
                }
    int ans=Inf;
    for(int i=0;i<=2*tot;++i){
        if(dp[0][0][i])
            ans=std::min(ans,abs(i-tot));
        if(dp[0][1][i])
            ans=std::min(ans,abs(i-tot));
    }
    printf("%d
",ans);
}
int main(){
    Init();
    Solve();
    return 0;
}