1. 差分数组
- 差分数组的定义:记录当前位置的数与上一位置的数的差值.
| 原数组 (a_i) | 9 | 4 | 7 | 5 | 9 |
|---|---|---|---|---|---|
| 差分数组 (b_i) | 9 | -5 | 3 | -2 | 4 |
| 差分数组的前缀和 | 9 | 4 | 7 | 5 | 9 |
-
显然:(a_i=sum_{j=1}^i b_j)
-
差分数组能够高效的解决区间修改单点查询的问题。
-
比如我们对区间
[2,4]每个元素加上5,我们只需在差分数组:(b_2+=5,b_5-=5) ,然后求前缀和即可原数组 (a_i) 9 4 7 5 9 差分数组 (b_i) 9 0 3 -2 -1 差分数组的前缀和 9 9 12 10 9
-
-
差分数组很容易算出前缀和:
- (sum_x=sum_{i=1}^x a_i) = (sum_{i=1}^x sum_{j=1}^i b_i)
- 容易发现,(b_1)使用了(x) 次,(b_2) 使用了 (x-1) 次,(b_3) 使用了 (x-2) 次……
- 因此可得:(sum_x = sum_{i=1}^x (x-i+1)*b_i) 。
2. 树上差分
1. 相关概念
- 树的以下两个性质:
- 任意两个节点之间有且只有一条路径。
- 根节点确定时,一个节点只有一个父亲节点。
- 这两个性质都很容易证明。那么我们知道,如果假设我们要考虑的是从
u到v的路径,u与v的lca是a,那么很明显,如果路径中有一点u′已经被访问了,且u′≠a,那么u'的父亲也一定会被访问,这是根据以上性质可以推出的。 - 所以,我们可以将路径拆分成两条链,
u->a和a->v。 - 树上差分有什么作用?举个例子,如果题目要求对树上的一段路径进行操作,并询问某个点或某条边被经过的次数,树上差分就可以派上用场了。这就是树上差分的基本操作。
- 树上差分,就是利用差分的性质,对路径上的重要节点进行修改(而不是暴力全改),作为其差分数组的值,最后在求值时,利用dfsdfs遍历求出差分数组的前缀和,就可以达到降低复杂度的目的。
2. 点差分
-
如何给树上的一条链
x ~ y每个点+1呢?(假设x为y的祖先)-
我们还是需要回到差分数组来进行考虑。设原数组为
a,差分数组为d。 -
假如给
d[i]+1,其实就相当于给a[i]~a[n]每个元素+1((a[i]=sum_{j=1}^i d[j]))。 -
那么,如果给树上的一个节点
x的d[x] +1,那它表示给哪一段区间的a +1呢?子树? 但子树中可能有很多条链啊,总不能去记录这次+1对应哪一条链吧。所以,这条链只能是x到根节点这条链! -
所以,
d[x]+1,相当于a[root]~a[x]链上的每个节点都+1。 -
回到上面的问题——如何区间修改?
-
先考虑简单的情况,当
x是y的祖先时。 -
这个问题的答案应该就很明显了:
d[fa[x]]−1,d[y]+1(fa[x]表示x的父亲) -
相当于:
a[y] ~ a[root]的链元素+1,a[fa[x]] ~ a[root]链的元素−1,发现a[fa[x]] ~ a[root]这段区间其实加一完之后又减了一,所以他们并没有改变,于是就实现了a[y] ~ a[x]这段区间+1。 -
如果
x不是y的祖先,假设a=lca(x,y)。-
很容易想到把链
x~y分成两个链,x~a和a~y。即d[x]+1,d[y]+1。 -
但这样链
a~root增加了2,我们让d[a]-1,此时fa[a]~root变成了-1,需要d[fa[a]]-1完美解决。
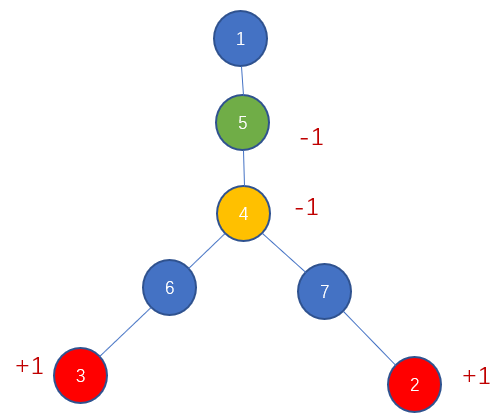
-
-
要想知道点
i被修改了多少,即为节点i所有子节点差分之和加上当前节点的差分。
-
-
-
例题:松鼠的新家(
luogu p3258)Description
- 松鼠的新家是一棵树,前几天刚刚装修了新家,新家有
n个房间,并且有n-1根树枝连接,每个房间都可以相互到达,且俩个房间之间的路线都是唯一的。天哪,他居然真的住在“树”上。 - 松鼠想邀请小熊前来参观,并且还指定一份参观指南,他希望小熊能够按照他的指南顺序,先去 (a_1),再去 (a_2),……,最后到 (a_n),去参观新家。可是这样会导致重复走很多房间,懒惰的维尼不停地推辞。可是松鼠告诉他,每走到一个房间,他就可以从房间拿一块糖果吃。
- 小熊是个馋家伙,立马就答应了。现在松鼠希望知道为了保证维尼有糖果吃,他需要在每一个房间各放至少多少个糖果。
- 因为松鼠参观指南上的最后一个房间 (a_n) 是餐厅,餐厅里他准备了丰盛的大餐,所以当维尼在参观的最后到达餐厅时就不需要再拿糖果吃了。
Input
-
第一行一个正整数
n,表示房间个数 -
第二行
n个正整数,依次描述 (a_1, a_2,cdots,a_n)。 -
接下来
n-1行,每行两个正整数x,y,表示标号x和y的两个房间之间有树枝相连。
Output
- 一共
n行,第i行输出标号为i的房间至少需要放多少个糖果,才能让小熊有糖果吃。
Input
5 1 4 5 3 2 1 2 2 4 2 3 4 5output
1 2 1 2 1Hint
- 对于全部的数据,(2 le n le 3 imes 10^5, 1 le a_i le n)。
- 松鼠的新家是一棵树,前几天刚刚装修了新家,新家有
-
分析:
-
小熊从房间
u到达房间v,其路径上的每个房间都需要准备一颗糖,很容易想到树上差分。 -
路径
1~4,4~5中间的4号房间只需一个糖果,还有最后的房间2也不需要放糖果,所以需要减去1 -
Code#include <bits/stdc++.h> const int maxn=3e5+5; struct edge{ int to,next; }e[2*maxn]; int n,len; int a[maxn],head[maxn],deep[maxn],f[maxn][21],sum[maxn]; void Insert(int u,int v){ e[++len].to=v;e[len].next=head[u];head[u]=len; } void dfs(int u,int fa){ deep[u]=deep[fa]+1;f[u][0]=fa; for(int i=1;(1<<i)<=deep[u];i++) f[u][i]=f[f[u][i-1]][i-1]; for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(v!=fa)dfs(v,u); } } int lca(int u,int v){ if(deep[u]<deep[v])std::swap(u,v); int len=deep[u]-deep[v],k=0; while(len){ if(len & 1)u=f[u][k]; ++k;len>>=1; } if(u==v) return u; for(int i=20;i>=0;i--){ if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i]; } return f[u][0]; } void search(int u){//求每个节点的差分和 for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(v==f[u][0]) continue; search(v); sum[u]+=sum[v]; } } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n-1;i++){ int u,v;scanf("%d%d",&u,&v); Insert(u,v);Insert(v,u); } dfs(1,0); for(int i=1;i<=n-1;i++){ int x=a[i],y=a[i+1],LCA=lca(x,y); sum[x]++; sum[y]++; sum[LCA]--; sum[f[LCA][0]]--; } search(1); for(int i=2;i<=n;i++)//除了起点,其他的需要减去1 sum[a[i]]--; for(int i=1;i<=n;i++) printf("%d ",sum[i]); return 0; }
-
3. 边差分
-
用
cf[i]代表从i到i的父亲这一条路径经过的次数。令a=lca(u,v)因为关于边的差分,a表示a到其父亲的那条边,不在u~v路径中,所以cf[u]++,cf[v]++,cf[a]−=2。 -
例题:
luogu P2680运输计划 -
题意:一棵树上有
m条道路,可以使任意一条道路的权值变为0,怎样使长度最长的道路长度最小。 -
分析:
-
很容易想到,找到这
m条路径中最长的一条,并把路径上最长的边归零,但改变一条边,可能多条路径的长度也要改变,而且不是一定要把最长的边归零就一定最好。 -
我们可以二分最终答案,答案肯定在
0~maxl(maxl表示最长路径长度)之间。我们需要修改的是现在路径长度超过mid的链中的边,那具体修改那条边呢? -
假设长度超过
mid的路径有cnt条,显然我们修改的这条边必须同时影响着cnt条链,即这条边必须为这cnt条链都经过。否则修改无意义。 -
所以我们二分答案,把经过了
cnt次的边中长度最大的边归零,判断这cnt条边中最长的链-归零边<=mid。 -
判断一条边被经过了多少次,正好用树上差分的边差分。
-
Code#include <bits/stdc++.h> const int maxn=3e5+5; int f[maxn][22],head[maxn],edge[maxn],deep[maxn],dis[maxn]; int st[maxn],ed[maxn],c[maxn],lca[maxn],len[maxn]; int n,m,lene,maxl,ans,cnt,cutedge; struct Edge{int to,w,next;}e[maxn<<1]; void Insert(int x,int y,int z){ e[++lene].to=y;e[lene].w=z;e[lene].next=head[x];head[x]=lene; } void dfs(int u){//预处理 deep[u]=deep[f[u][0]]+1; for(int i=1;(1<<i)<=deep[u];i++) f[u][i]=f[f[u][i-1]][i-1]; for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(v==f[u][0])continue; f[v][0]=u; edge[v]=e[i].w;//edge[v]记录v到父节点u的边长 dis[v]=dis[u]+e[i].w;//求解v到根节点的距离 dfs(v); } } int Lca(int u,int v){ if(deep[u]<deep[v])std::swap(u,v); int len=deep[u]-deep[v],k=0; while(len){ if(len & 1)u=f[u][k]; ++k;len>>=1; } if(u==v)return u; for(int i=20;i>=0;i--) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i]; return f[u][0]; } int dist(int i){//求出第i条路径的长度 return dis[st[i]]+dis[ed[i]]-2*dis[lca[i]]; } int dfs2(int u){ int tot=c[u];//计算u到其父亲这条边访问次数 for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(v==f[u][0])continue; tot+=dfs2(v); } if(tot==cnt)//计算经过cnt次最长的边 cutedge=std::max(cutedge,edge[u]); return tot; } bool check(int mid){ cnt=0;cutedge=0;//cnt记录超过mid的路径数,cutedge记录要删掉的边 for(int i=1;i<=n;i++)c[i]=0;//差分数组清零 for(int i=1;i<=m;i++) if(len[i]>mid){//超出mid的区间进行差分,并计数 cnt++;c[st[i]]++;c[ed[i]]++;c[lca[i]]-=2; } if(cnt==0)return 1;//没有超过的 dfs2(1);//求出被经过cnt次,且最长的边 return maxl-cutedge<=mid; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<n;i++){ int u,v,w;scanf("%d%d%d",&u,&v,&w); Insert(u,v,w);Insert(v,u,w); } dfs(1); for(int i=1;i<=m;i++){ scanf("%d%d",&st[i],&ed[i]); lca[i]=Lca(st[i],ed[i]); len[i]=dist(i); maxl=std::max(maxl,len[i]); } int l=0,r=maxl;//最短时间在[0,maxl]之间 while(l<=r){ int mid=(l+r)>>1; if(check(mid))ans=mid,r=mid-1; else l=mid+1; } printf("%d ",ans); return 0; }
-