一文读懂ECDSA算法如何保护数据

学习区块链，总是无法避开各种加密算法，因为各种加密算法在实现区块链当中的各个环节都有着不可替代的作用。这里介绍一下在比特币以及以太坊当中被大量使用基于离散对数数学难题的ECDSA算法。

本文主要翻译自这篇文章Understanding how ECDSA protects your data

每个人可能都听说过ECDSA算法。当我提到数字签名的时候，有些人能够很好地识别出它，有些人却不知道我说的是什么。

我曾经试图去理解ECDSA是如何工作的，但是大部分的在线参考资料都是有缺失的，不足以让我能够很好地理解它。他们要么太基础了──只是解释算法的基础然后留给你“它是如何工作的？”的疑问──要么就是太高阶了，完全略过那些你本该知道但它却假设你已经知道的基础知识。因此，你始终在“它是如何工作的”和“我们如何才能够理解它的工作原理之间”徘徊。如果你没有一个数学或者密码学的学位，但是依然想知道它到底是如何工作的，而不是“魔术发生了，签名被确认了”，那么你运气不够好，因为哪里都没有“新手ECDSA”的教程。

我决定对ECDSA进行研究，以便更好地了解它是如何保护我的数据以及实际上它有多安全。在做了大量的研究工作并最终弄清楚以后，我打算写一篇文章来解释ECDSA是如何工作的，具体算法是如何实现的，以及一个数字签名是如何进行确认的且在它被确认以后是如何确保它是不可伪造的。说实话，要了解以上所有内容并不容易，但是我将尽我的最大努力进行解释，并且对于读者所应该掌握的知识进行最小的假设，希望所有的人都能够看懂。

Step 1: What is ECDSA？

ECDSA是Elliptic Curve Digital Signature Algorithm【椭圆曲线数字签名算法】的简称，主要用于对数据（比如一个文件）创建数字签名，以便于你在不破坏它的安全性的前提下对它的真实性进行验证。可以将它想象成一个实际的签名，你可以识别部分人的签名，但是你无法在别人不知道的情况下伪造它。而ECDSA签名和真实签名的区别在于，伪造ECDSA签名是根本不可能的。

你不应该将ECDSA与用来对数据进行加密的AES（高级加密标准）相混淆。ECDSA不会对数据进行加密、或阻止别人看到或访问你的数据，它可以防止的是确保数据没有被篡改。

ECDSA当中有两个词需要注意：Curve（曲线）和Algorithm（算法），这意味着ECDSA基本上是基于数学的。并且，这些涉及非常复杂的数学原理。因此，即便我尽力试着进行简单化处理以让非技术背景的人也能够理解，为了更好地理解你依然需要一些数学方面的背景知识。我将分两部分讲这部分的内容，首先是对它具体的工作原理进行解释，然后深入其内部工作机理助于你的理解。需要注意的是，虽然我已经很好地理解ECDSA，但我不是这方面的专家，不过这篇文档还是由相关专家审议过的。

Step 2: Understanding the Basics

原理非常简单，有一个数学方程，在图上画了一条曲线，然后你在这条曲线上面随机选取了一个点作为你的原点(point of origin)。接着你产生了一个随机数，作为你的星辰，最后你用上面的随机数和原点通过一些复杂的魔法数学方程得到该条曲线上面的第二个点，这是你的公钥(Public key)。

当你想要对一个文件进行签名的时候，你会用这个私钥（随机数）和文件的哈希（一串独一无二的代表该文件的数）组成一个魔法数学方程，这将给出你的签名。签名本身将被分成两部分，称为R和S。为了验证签名的正确性，你只需要公钥（用私钥在曲线上面产生的点）并将公钥和签名的一部分S一起代入另外一个方程，如果这个签名是由私钥正确签名过的数字签名，那么它将给出签名的另外一部分R。简单来说，一个数字签名包含两个数字，R和S，然后你使用一个私钥来产生R和S，如果将公钥和S代入被选定的魔法数学方程给出R的话，这个签名就是有效的。仅仅知道公钥是无法知道私钥或者创建出数字签名。

Step 3: Why Use ECDSA？

现在你可能知道一些基础，但是还不是特别理解，毕竟它还是太复杂了，公钥、私钥这些，都是什么东西呢？不必担心，我很快会进行具体解释。在这之前，我先介绍下为什么我们使用ECDSA以及其具体的应用场景。

除了显而易见的“我需要对一份文件/合同进行签名”，还有一个非常流行的应用场景：让我们以一个不想自己的数据被用户修改或者破坏的应用程序为例，比如一个只允许你载入官方地图和不可修改的模块的游戏，或者一部只允许你安装官方应用程序的手机或其它设备。

在这些案例当中，相关文件（应用程序、游戏地图、数据等）会用ECDSA进行签名，公钥会随应用程序/游戏/设备一起捆绑并用来验证签名来确保数据没有被修改，而私钥在本地一个私密的地方进行保存。由于你可以用公钥对签名进行验证，但是不能用它创建或者伪造新的签名，你可以无所顾忌地将公钥随应用程序/游戏/设备一起分发。

这与AES相比，区别是显而易见的。AES加密系统允许你对数据进行加密，但是你需要用密钥来解密，这就要求你将密钥与应用程序一起捆绑，破坏了对数据进行保护防止数据被用户修改的目的。

一个很好的例子就是PS3的控制台，它被大量的破解，所有的文件可以解密，所有的密钥可以从解密的文件当中抽取，但是为了能够在最新的固件上面运行程序，你还需要破解一个ECDSA的数字签名。

Step 4: Basic Mathematics and Binary

让我们从一些最基本的开始，如果你已经知道了会觉得很无聊，但是对于不知道的人则是必须了解的：ECDSA只使用整数数学，没有浮点数，这意味着可能的数值是1，2，3……，1.5，2.5……则是不被允许的，并且，整数的范围由签名当中所采用的位数决定，更多的位数意味着更大的数字范围，更高的安全性能，因为这使得“猜”到方程当中所采用的具体数字变得更难。正如你所应该知道的，计算机采用比特来表示数据，一个比特是二进制当中的一位，八个比特表示一个字节。每次你增加一个比特，可表示的最大整数就可以翻一倍，使用4个比特，你可以表示0~15，一共16个数字，5个比特，你可以表示32个数字，6个比特，可以表示64个数字……一个字节，可以表示256个数字，32比特，可以表示4294967296个数字……通常ECDSA会总共使用160比特，它可以表示相当大的数，可以由49个数字在里面。

另外一个需要知道的数学组成是模运算，可以简单地说是整数求除之后的余数。举个例子，x mod 10是指 x除以10以后的余数，这个余数总是在0和10之间，142 mod 10 的结果是2 。另外一个例子，对于 x mod 2的结果，如果 x 偶数则结果为0，如果 x 奇数则结果为1。

Step5：The Hash

ECDSA与消息的SHA-1加密哈希一起使用来对文件进行签名。一个哈希是你作用于数据的每一个字节然后给你一个代替该数据的整数的另外一个数学函数。举个例子，所有字节所代表的数值之和可以被认为是一个非常简单的哈希函数。于是，消息或文件当中任何修改，整个哈希就会变得完全不同。在SHA1哈希算法当中，它的输出结果总是20字节，即160比特。在验证文件是否被修改或者破坏，它非常有用，你可以得到任意大小的文件的20字节的哈希，并且你可以非常方便的重新计算哈希以确认他们是否匹配得上。而ECDSA所签名的正是那个哈希，因此，如果文件或者数据发生了改变，哈希就会发生改变，然后签名失效了。

为了便于理解，让我们举一个例子。我们用一个最简单的哈希函数：将所有的数据求和再对10取模运算。

第一步，你必须理解所有的数据将用整数来进行表示。一个文本文件就是一系列的字节，正如我们之前所解释的，一个字节表示8个比特，可以表示0_{255之间的一个数。因此，如果我们用一个整数来表示每一个字节，并且将文件的每一个字节所代表的数相加，然后将求和后的结果对10取模，我们将能够得到一个0}9之间的数作为最终的结果哈希。对于相同的数据我们将总是得到相同的结果，并且假如你修改了文件中的一个字节，结果将会不同。当然，你也知道，因为这个哈希函数的输出空间只有0~9这10种可能性，你想要获得相同的输出，可以非常容易的通过修改文件内容得到，因此，修改文件内容将有1/10的概率得到相同的哈希。

这是SHA1出来扮演重要角色的地方，SHA1算法比起我们刚才简单的“对10取模”的哈希函数要复杂复杂得多，它将给出一个非常巨大的数（160位或者比特，如果用十进制表示的话将由49个数字组成），并且随着文件的一点细微的小变化，它也能够产生显著的变化。

这个不可预测的特性让SHA1算法成为一个非常好的哈希算法，非常安全且产生“碰撞(collision)”（两个不同文件有相同的哈希）的可能性非常低，使得通过伪造数据获得特定的哈希的变得不可能。

Step6: The ECDSA Equation

好了，那到底ECDSA是如何工作的呢？椭圆曲线密码学是基于以下形式的方程：

第一点你需要注意的是这里有一个取模运算，然后 y 是进行了平方处理，另外也别忘记这是一条曲线的方程。这意味着对于所有的 x 坐标（x只能取整数），你可以得到两个 y 的值，且曲线关于 X 轴对称。取模运算的底是一个素数且确保所有得到的数值在160比特所能够表示的范围之内，允许采用模平方根和模的乘法逆元来简化运算。因为我们以 p 为模的底，这意味着 y 可能的取值在0~p-1之间，一共有 p 个可能的值空间。不过，因为我们只能处理整数，只有一部分取值能够满足完美平方数（两个整数的平方值）的要求，我们只能在曲线上面得到 N 个可能的点，且满足$N

因为每一个 x 可以得到两个曲线上的点（y^2 的两个正负平方根），这意味着一共有 N/2 个可行的 x 坐标是有效的，并在曲线上面给出相关的点。且因为整数运算和模运算的存在，这条椭圆曲线上面只有有限个点。

哈哈，是不是有点难，有点复杂，在继续之前，让我们先总结一下。ECDSA方程给出了而一条曲线，这条曲线上面一共有 N 个有效的点，因为 Y 轴的取值区间由模底 p 来确定，并且需要满足完美平方（ Y^2 ）并关于 X 轴对称。我们一共有 N/2 个有效的 x 坐标，最后还有满足$N

Step 7: Point Addition

关于椭圆曲线需要了解的另外一个事情是椭圆曲线点加法的表示方法。它是这样定义的：将一个点 P 和另外一个点 Q 相加将得到点 S ，如果我们从 P 到 S 画一条线，并延长与曲线相交于第三个点 R ，则 R 为 S 的负值，别忘记曲线是关于 X 轴对称的。在这种情况下，我们定义 R=-S 来表示R在 X轴上面的对称点。具体可以看下面这张图。

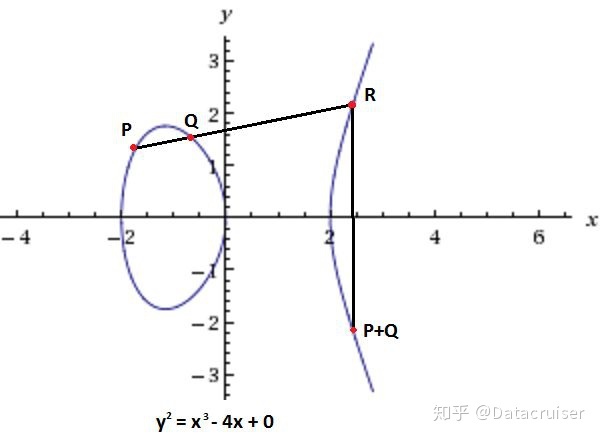
这是令 a=-4, b=0以后的椭圆曲线，关于X轴对称，P+Q是 R关于 X轴上面的对称点，且R是从P到 Q连线延长线与曲线的第三个交叉点。

Step8: Point Multiplication

同样的机制，如果你进行P+P，X轴的对称点，然后P+P+P可以看作是P+P点与 P点相加的结果。这就可以用来对椭圆曲线点乘法进行定义：k * P就是点P自身进行k次相加，以以下两幅图为例。

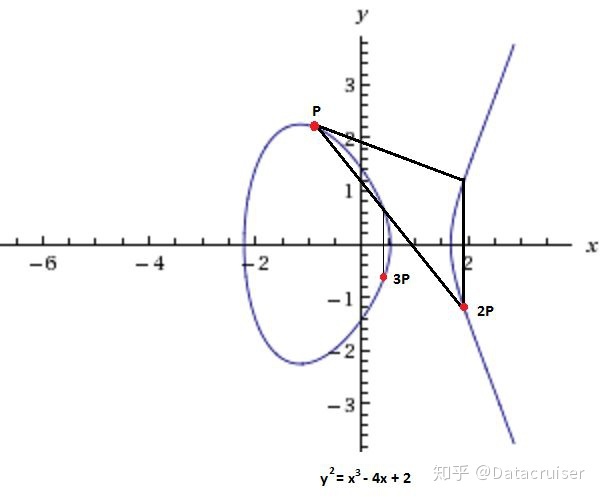
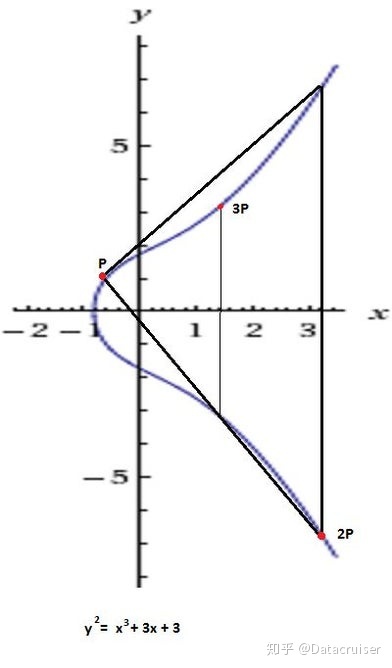
这里你可以看到两个椭圆曲线和一个用来作切线的点P，它与曲线相交于第三点，然后其对称点是2P，接着从这个点开始，你画一条从2P到 P的直线与曲线相交，交点的对称点为3P。你可以类推一直做下去来完成椭圆曲线乘法。你也可以猜出为什么在做加法时需要取R的对称点，因为只有这样，才可以避免在做同一点的多次加法的时候得到同一条线和相同的三个交点。

Step 9: The Trap Door Function!

一个椭圆曲线乘法的特性是你有一个点R = k * P，你知道R和 P，但是你无法据此求出k，因为这里并没有椭圆曲线减法或者椭圆曲线除法可用，你并不能通过 k=R/P得到k。并且，因为你可以做成千上万次的加法，最终你只是知道在曲线上面结束的点，但是具体是如何到达这个点你也并不知道。你无法进行反向操作，得到与点P相乘以后给你点R的k。

这种即便你知道原点和终点，但是无法知道被乘数是ECDSA算法背后安全性的所有基础，而这一原则也被称为单向陷门函数。

Step 10: The ECDSA Algorithm

现在已经掌握了基础，现在让我们来谈谈实际的ECDSA签名算法。

对于ECDSA算法，首先你需要知道你的曲线参数，一共有a,b,p,N,G，你已经了解a和b是曲线方程的参数（ p是模运算的底，N是曲线上面点的个数，对于ECDSA，还需要一个参数G，它表示一个你所选中的一个参考的起始点。它可以是曲线上面的任意一点。

这些曲线参数非常重要，如果不能够事先获得它们，你显然无法签署或者验证一个签名。是的，验证一个签名并不只是知道公钥，你还需要知道这个公钥是从什么曲线参数推算出来的。NIST(National Institute of Standards and Technology)和SECG(Standards for Efficient Cryptography Group)已经提供了预处理的已知高效和安全的标准化曲线参数。

总结一下：首先，你有一对密钥：公钥和私钥，私钥是一个随机数，也是160比特大小，公钥是将曲线上的点G与私钥相乘以后的曲线上的点。令dA表示私钥，一个随机数，Qa表示公钥，曲线上面的一个点，我们有Qa = dA XG，其中G是曲线上面的参考点。

Step 11: Creating a Signature

下面的问题来了，那么我们是如何对一个文件或者一个信息进行签名的呢？

第一步，你需要知道签名本身是40字节，由各20字节的两个值来进行表示，第一个值叫作R，第二个叫作s。值对(R, S)放到一起就是你的ECDSA签名。

然后来看看为了进行签名如何创建这一值对：

产生一个随机数k，20字节
利用点乘法计算 P = k * G
点P的 x坐标即为R
利用SHA1计算信息的哈希，得到一个20字节的巨大的整数z
利用方程S = k^-1 * (z + dA * R) mod p计算S
其中k是用来生成R的随机数，k^-1是 k的模的乘法逆元。

Step 12: Verifying the Signature

好了，现在有了你的签名，你想要来验证它，也非常的简单，你只需要公钥和导出这个公钥的曲线参数就可以了。你用以下方程来计算点P：

如果点P的 x坐标与R相等，则意味着这个签名是有效的，否则是无效的。

非常简单，下面来看看如何一步一步从数学上面进行推导的。

首先，我们有：

由于

代入上式，则有：

\[% MathType!MTEF!2!1!+- % feaagGart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaacaWGqbGaeyypa0Jaam4uamaaCaaaleqa % baGaeyOeI0IaaGymaaaakiabgEna0kaadQhacqGHxdaTcaWGhbGaey % 4kaSIaam4uamaaCaaaleqabaGaeyOeI0IaaGymaaaakiabgEna0kaa % dkfacqGHxdaTcaWGKbGaamyqaiabgEna0kaadEeacqGH9aqpcaWGtb % WaaWbaaSqabeaacqGHsislcaaIXaaaaOGaaiikaiaadQhacqGHRaWk % caWGKbGaamyyaiabgEna0kaadkfacaGGPaGaey41aqRaam4raaaa!6572! P = {S^{ - 1}} \times z \times G + {S^{ - 1}} \times R \times dA \times G = {S^{ - 1}}(z + dA \times R) \times G \]

再由点P的 x坐标必须与R匹配，且R是点k * P的 x坐标，即 P = k * G，于是有：

两边将G拿掉，有：

两边求逆，即：

最后这个就是之前用来产生签名的方程，这是相匹配的，这是我们可以采用本节开头给出的方程进行签名验证的原因。

Step13: The Security of ECDSA

你可以注意到你需要同时知道随机数k和私钥dA才能够计算出S，但是你需要R和公钥Qa来对签名进行确认和验证。并且由于R=K * g以及Qa = dA * G 再加上ECDSA点乘法当中的单向陷门函数的特性（在Step9中进行过解释），我们无法通过Qa和 R来计算dA或 k，这使得ECDSA算法非常安全，没有办法找到私钥，也无法在不知道私钥的情况下伪造签名。

Step14: The Importance of a Random K

现在我们来讨论一下索尼PS3中使用的ECDSA签名是如何以及为什么产生问题的，以及它是如何允许黑客访问PS3的ECDSA的私钥的。

你还记得产生一个签名的两个方程，R = K * G 以及

这些方程的强势在于实际上有一个方程里面有两个未知数（ k和 dA），因此你是无法确定其中的任意一个。

话又说回来，算法的安全是基于其实现的。确保随机数k确实是随机产生的变得非常重要，并且没有人能够猜测、计算或者其它任何类型的攻击来得到随机数。但是索尼在它们的实现当中犯了一个巨大的错误，它们在任何地方都采用了同一个随机数，然后它们将具有相同的R，这意味着你可以使用两个分别具有散列z和 z'和签名S和 S'的两个文件的S签名来计算随机数k：

\[% MathType!MTEF!2!1!+- % feaagGart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakqGabeqaaWpabaGaam4uaiabgkHiTiaadofa % caGGNaaabaGaeyypa0Jaam4AamaaCaaaleqabaGaeyOeI0IaaGymaa % aakiaacIcacaWG6bGaey4kaSIaamizaiaadgeacqGHxdaTcaWGsbGa % aiykaiabgkHiTiaadUgadaahaaWcbeqaaiabgkHiTiaaigdaaaGcca % GGOaGaamOEaiaacEcacqGHRaWkcaWGKbGaamyqaiabgEna0kaadkfa % caGGPaaabaGaeyypa0Jaam4AamaaCaaaleqabaGaeyOeI0IaaGymaa % aakiaacIcacaWG6bGaey4kaSIaamizaiaadgeacqGHxdaTcaWGsbGa % eyOeI0IaamOEaiaacEcacqGHRaWkcaWGKbGaamyqaiabgEna0kaadk % facaGGPaaabaGaeyypa0Jaam4AamaaCaaaleqabaGaeyOeI0IaaGym % aaaakiaacIcacaWG6bGaeyOeI0IaamOEaiaacEcacaGGPaaaaaa!77E0! \begin{array}{l} S - S'\\ = {k^{ - 1}}(z + dA \times R) - {k^{ - 1}}(z' + dA \times R)\\ = {k^{ - 1}}(z + dA \times R - z' + dA \times R)\\ = {k^{ - 1}}(z - z') \end{array} \]

于是有：

一旦你知道了随机数k，求解S的方程就变成了一个只含一个未知数的方程，然后可以很容易地解出dA：

而一旦你知道了私钥dA，你现在可以签署自己的文件，PS3将承认它是一个由索尼签署的官方文件。这就是为什么重要的是要确保用于生成签名的随机数实际上是“加密随机的”。这也是为什么不可能有一个3.56版本以上的自定义固件的原因，因为自从3.56版本以来，索尼已经修复了他们的ECDSA算法实现，并使用了新的密钥，现在不可能这么容易找到私钥。

这个问题的另一个例子是，一些比特币客户使用非加密随机数生成器（在一些浏览器和一些Android客户机上），导致他们以相同的随机数k来签署交易，恶意用户能够据此找到他们比特币钱包的私钥并窃取他们的资金。

这表明了每次签名时使用真正随机数的重要性，因为如果(R,S)签名对的R值在两个不同签名上相同，则会暴露私钥。

下图展示了一个关于随机数的笑话。

当然，只要实现是正确合理的，ECDSA算法非常安全，不可能找到私钥。如果有办法很容易找到私钥，那么每台计算机、网站、系统的安全都可能受到危害，因为很多系统都依赖ECDSA来保证安全，而且不可能破解。

Step15: Conclusion

终于！我希望这能让很多人更清楚整个算法。我知道这仍然很复杂、很难理解。我试图让非技术人员更容易理解，但这个算法太复杂，无法用任何简单的术语解释。

但是，如果你是一个开发人员或数学家，或者有兴趣学习这方面的知识，因为你想帮助或简单地获得知识，那么我确信这包含了足够的信息，你可以开始学习，或者至少理解这个名为ECDSA的未知野兽背后的概念。

尽管如此，我还是要感谢一些帮助我理解这一切的人，特别是希望保持匿名的人，以及我在这篇文章中链接到的许多维基百科页面，还有Avi Kak，感谢他解释ECDSA背后的数学的论文，我从中借用了上面的这些图片。