扩展KMP(Z函数)

用途

(O(n))求一个串与另一个串的每一个后缀的LCP长度

算法过程

其实个人感觉跟KMP关系不大，反倒与Manacher有异曲同工之妙

求解Z函数

定义

s(i,j)：字符串(S)的第(i)为到第(j)位

suf(i)：以 (i) 开头的后缀，即(s(i,n))

z[i]：s(1,n)与(suf(i))的LCP长度，(z[1]=n)

r：当前匹配过的最靠右的点

考虑已知(z[1]sim z[i-1])，求出(z[i])

第一种情况

(i>r)，直接从(0)开始暴力匹配

第二种情况

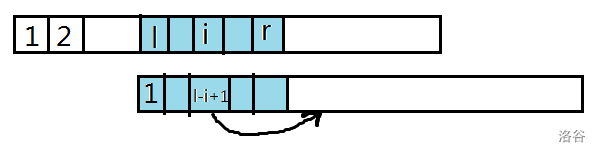
当前(s(l,r))对应匹配(s(1,r-l+1))，如图中蓝色部分所示

(i)对应的位置是(i-l+1)，如果(z[i-l+1])不超过(r-i+1)，那么(z[i-l+1])一定是合法的，直接赋值

第三种情况

(i)对应的位置是(i-l+1)，如果(z[i-l+1])超过(r-i+1)，那么(r-i+1)以内的一定是合法的，剩下的需要暴力判一判

代码

inline void getz(char *s,int n){
	memset(z+1,0,n<<2);
    z[1]=n;len=n;
	for(int i=2,l=0,r=0;i<=n;++i){
		if(i<=r)z[i]=min(z[i-l+1],r-i+1);
		while(i+z[i]<=n&&s[i+z[i]]==s[z[i]+1])++z[i];
		if(i+z[i]-1>r)l=i,r=i+z[i]-1;
	}
}

求一个串与另一个串的每一个后缀的LCP长度

与求Z函数类似

inline void calc(char *s,char *a,int n,int *ans){
	memset(ans+1,0,n<<2);
	for(int i=1,l=0,r=0;i<=n;++i){
		if(i<=r)ans[i]=min(z[i-l+1],r-i+1);
		while(i+ans[i]<=n&&ans[i]+1<=len&&a[i+ans[i]]==s[ans[i]+1])++ans[i];
		if(i+ans[i]-1>r)l=i,r=i+ans[i]-1;
	}
}

例题

CF1313E Concatenation with intersection

设(f_i)表示(a[i])与(s)的LCP长度，(g_i)表示(b[i])与(s)的LCS长度，这两个可以(O(n))使用exKMP求

转化题意为满足以下四个条件的(f_i+g_j-m+1)之和

(ile j)
(i+m-1>j)
(f_i>0,g_j>0)
(f_i+g_jge m)

对第二个限制容斥一下，先不考虑第二个限制，减去(jge i+m-1)的贡献

考虑维护(g_jge max(1,m-f_i))的(f_i+g_j-m+1)之和

将(f_i)与(g_j)拆开，两个树状数组(T1,T2)，分别维护(g_jge max(1,m-f_i))的(g_j)之和的(j)的个数，满足(g_jge max(1,m-f_i))的(g_j)之和

贡献为((f_i-m+1) imes T1+T2)

注意到(a/b)不能把(s)占满，求出的(LCP/LSP)要与(m-1)取(min)