模型性能的度量
目标:已知样本((x_1, y_1),(x_2,y_2),...,(x_n, y_n)),要求拟合出一个模型(函数)(hat{f}),其预测值与样本实际值y的误差最小。
考虑到样本数据其实是采样,y并不是真实值本身,假设真实模型(函数)是f,则采样值(y=f(x)+epsilon),其中(epsilon) 代表噪音,其均值为0, 方差为(sigma^2)。
噪音(noise)
实际应用中的数据基本都是有干扰的,例如信用卡发放问题:
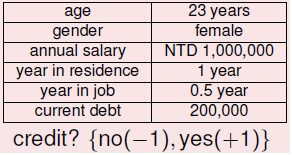
噪声产生的原因:
- 标记错误:应该发卡的客户标记成不卡,或者两个数据相同的客户一个发卡一个不发卡
- 输入错误:用户的数据本身就有错误,例如年收入少写一个0,性别写反了等
拟合函数(hat{f})的主要目的是希望它能对新的样本进行预测,所以,拟合出函数(hat{f})后,需要在测试集上检测其预测值与实际值y之间的误差。用平方误差函数(mean square error)来度量其拟合的好坏程度,即(((y-hat{f}(x))^2)
理解误差期望值
期望值的含义是指在同样的条件下重复多次随机试验,得到的所有可能状态的平均结果。对于机器学习,则是我们选择一种算法,以及设置一个固定的训练集大小(即所谓的特定的模型)。每次训练时从样本空间中选择一批样本作为训练集,但每次都随机抽取不同的样本,这样重复进行多次训练。每次训练会得到一个具体的模型,每个具体模型对同一个未见过的样本进行预测可以得到预测值。不断重复训练和预测,就能得到一系列预测值,根据样本和这些预测值计算出方差和偏差,可以帮助我们考察该特定模型的预测误差的期望值,衡量该特定模型的性能。通过对比多个特定模型的误差的期望值,可以帮助我们选择合适的模型。
举例说明如下:
假设真实模型为(f(x)=x+2sin(1.5x)),函数图像如下图曲线所示。样本值y就在真实值得基础上叠加一个随机噪音N(0,0.2)
import numpy as np
import math
from matplotlib import pyplot as plt
import random
x = np.arange(1, 10, 0.1)
y = [i+2*math.sin(1.5*i) for i in x]
index = random.sample(range(len(x)), 20)
x_samples = [x[i] for i in index]
y_samples = [y[i] + np.random.normal(0, 0.2, 1) for i in index]
plt.plot(x, y)
plt.scatter(x_samples, y_samples, marker='o', color='r')
plt.show()
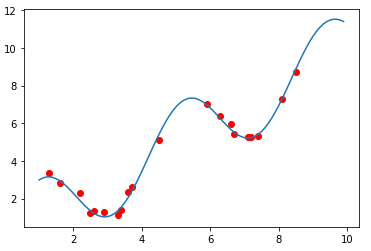
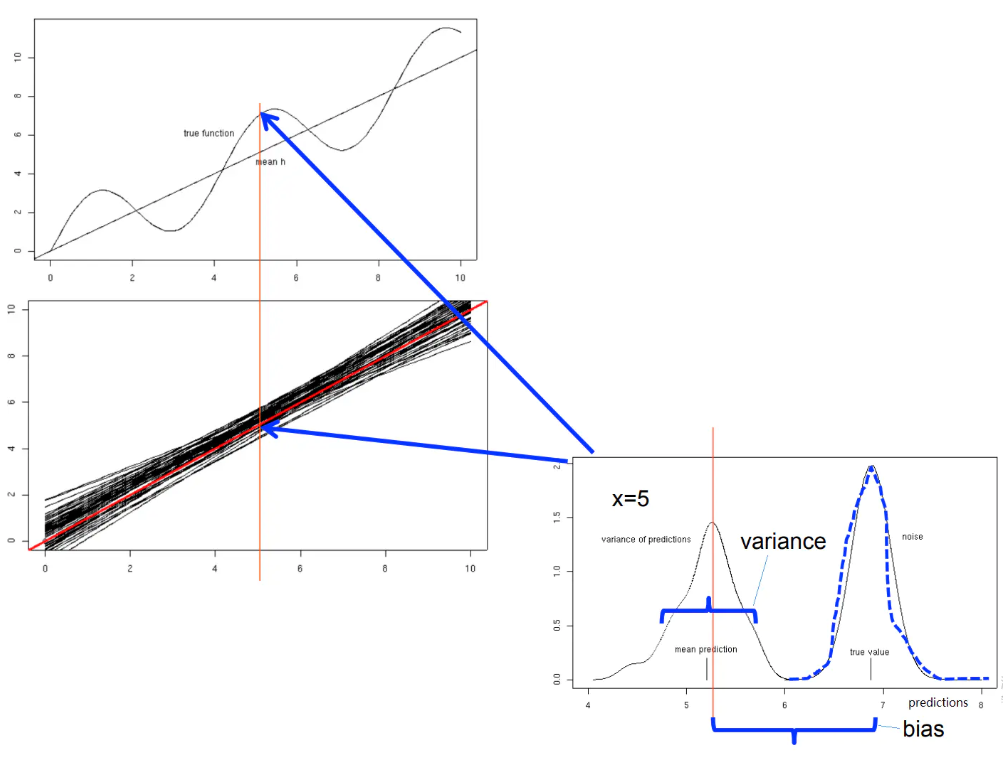
假设我们用线性函数来构建模型,训练样本为y((y=f(x)+epsilon))。经过多次重复,可以得到一系列具体的线性模型,如下图中那一组聚集在一起的黑色直线所示,其中间有一条红色线是这一组线性函数的平均(期望值)。这就是特定模型(线性函数)在同样条件下(每次取固定数个样本点)重复多次(得到50个线性函数)。
根据生成的50个具体的线性函数来考察该线性模型的预测性能,选取一个样本点,比如选择 x=5 时(下图中红色竖线位置),真实值f(x)=6.878, 样本y约等于6.876,y与f(x)的偏差体现在图片右下方的噪音部分。红色线性函数在x=5位置的值是这50个线性函数在该位置的期望值,黑色直线在x=5位置的一系列值得分布则反映了它们的方差(varaince)。50个预测的期望值与真实值f(x)之间的距离体现了偏差(bias)。
误差期望值的分解及公式推导
误差的期望值可以分解为三个部分:样本噪音、模型预测值的方差、预测值相对真实值的偏差
即误差的平方的期望 = 噪音的方差 + 模型预测值的方差 + 预测值相对真实值得偏差的平方
推导如下
真实模型(函数):(f=f(x))
拟合模型(函数):(hat{f}=hat{f}(x))
方差的计算公式:(Var[X] = E[X^2] - (E[X])^2)
测试样本值y的期望值: (E(y)=E(f+epsilon)=E(f)+E(epsilon)=E(f)=f)
测试样本值y的方差: (Var(y)= E[(y-E(y)^2]=E[(y-f)^2]=E[(f+epsilon-f)^2]=E(epsilon)^2=Var(epsilon)+(E(epsilon))^2=sigma^2)
误差的平方的期望公式推导如下:
使用特定模型对一个测试样本进行预测,就像打靶一样。
靶心(红点)是测试样本的真实值,测试样本的y(橙色点)是真实值加上噪音,特定模型重复多次训练会得到多个具体的模型,每一个具体模型对测试样本进行一次预测,就在靶上打出一个预测值(图上蓝色的点)。所有预测值的平均就是预测值的期望(较大的浅蓝色点),浅蓝色的圆圈表示预测值的离散程度,即预测值的方差。
所以,特定模型的预测值 与 真实值 的误差的 期望值,分解为上面公式中的三个部分,对应到图上的三条橙色线段:预测值的偏差、预测值的方差、样本噪音。

总之,在机器学习中考察偏差和方差,最重要的是要在不同数据集上训练出一组特定模型,对一个测试样本进行预测,考察这一组预测值的方差和偏差。
偏差-方差的选择
理想中,我们希望得到一个偏差和方差都很小的模型,但实际上往往很困难。
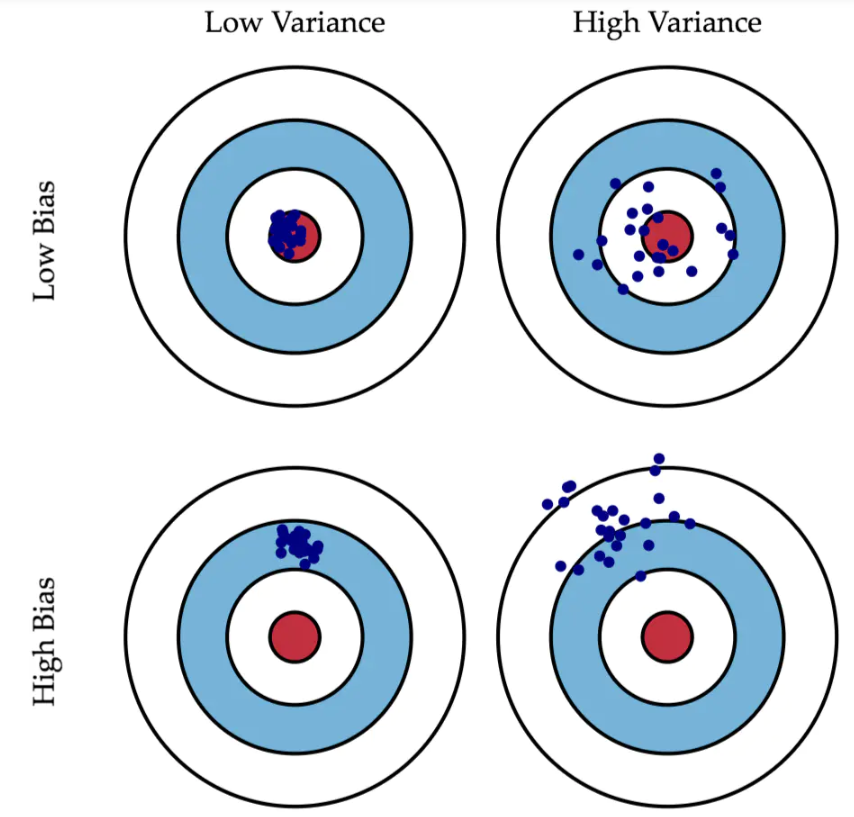
相对较好的模型的顺序:方差小,偏差小>方差小,偏差大>方差大,偏差小>方差大,偏差大。
方差小,偏差大之所以在实际中排位比较靠前,是因为它比较稳定。很多时候,实际中无法获得非常全面的数据集,那么,如果一个模型在可获得的样本上有较小的方差,说明它对不同数据集的敏感度不高,可以期望它对新数据集的预测效果比较稳定。