题目等级:Hard
题目描述:
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
You may assume nums1 and nums2 cannot be both empty.
Example 1:
nums1 = [1, 3]
nums2 = [2]
The median is 2.0
Example 2:
nums1 = [1, 2]
nums2 = [3, 4]
The median is (2 + 3)/2 = 2.5
题意:给定两个长度分别为m和n的有序数组,找到这两个数组所有元素的中位数。要求时间复杂度为O(log(m+n))。
解题思路:
本题属于困难等级,相对难度较大。这里由简单到复杂给出五种解法。
解法一:两个数组归并,找中位数
第一眼看到这个题目,我们就会有一个很直观的暴力解法。两个数组都是从小到大有序,要求整体的中位数,只需要将两个数组进行归并,合成一个递增的数组,则直接就可以找到中间元素。
两个数组归并的时间复杂度是O(m+n),有序数组中找中位数只需要O(1)的时间,所以总的时间复杂度是O(m+n),另外还需要一个长度为m+n的额外数组,因此空间复杂度也是O(m+n)。
代码如下:
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m = nums1==null?0:nums1.length;
int n = nums2==null?0:nums2.length;
if(m==0) //数组1空
return findMedianSortedArrays(nums2);
if(n==0) //数组2空
return findMedianSortedArrays(nums1);
int[] nums=new int[m+n];
int count=0;
for(int i=0,j=0;i<m || j<n;){ //合并为一个数组
if(i==m)
nums[count++]=nums2[j++];
else if(j==n)
nums[count++]=nums1[i++];
else{
if(nums1[i]<nums2[j])
nums[count++]=nums1[i++];
else
nums[count++]=nums2[j++];
}
}
return findMedianSortedArrays(nums);
}
//在一个有序数组中找中位数
public double findMedianSortedArrays(int[] nums){
int len=nums.length;
if(len%2==0)
return (nums[len/2]+nums[len/2-1])/2.0;
else
return nums[len/2];
}
解法二:改进的归并
从暴力法出发,我们其实可以发现,我们的目标只是找到中位数,因此完全没有必要将整个数组都归并完,我们只需要归并到可以得到中位数即可。也就是说:本来归并后的数组长度应该为m+n,但是只要归并到长度的一半就可以找到中位数。
对于中位数,如果len(len=m+n)是奇数,那么归并之后第len/2+1个数就是中位数;如果len是偶数,那么归并之后应该是两个中间数的平均值,也就是第len/2个数和第len/2+1个数两个数的均值。注意这里我们说的是第几个数,下标为0就是第1个数,写代码时要注意。
因此,解法二的思路就是只归并到可求出中位数为止,并且整个归并后的数组没有必要都保存,只需要在循环过程中维护两个变量即可,第len/2个数和第len/2+1个数。
由于只归并了一半,因此时间复杂度为O(len/2),也就是仍为O(m+n),但是空间复杂度降到了O(1)。
代码如下:
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m = nums1==null?0:nums1.length;
int n = nums2==null?0:nums2.length;
int i=0,j=0;
int first=-1,second=-1;
//不需要全部保存,只保存两个数即可
for(int count=0;count<=(m+n)/2;count++){ //找到中位数就停止
first=second;
if(i==m)
second=nums2[j++];
else if(j==n)
second=nums1[i++];
else{
if(nums1[i]<nums2[j])
second=nums1[i++];
else
second=nums2[j++];
}
}
if((m+n)%2==0)
return (first+second)/2.0;
else
return second;
}
解法三:找第k小的数字
很明显,解法一和二虽然比较容易理解,但是我们看到实际时间复杂度都没有达到题目的要求。题目要求时间复杂度为log级别,一般情况下,要想成为log时间复杂度,要么是与二叉树相关,要么是与二分查找有关。这里的数据结构是数组,因此,我们要在二分查找上面进行一些考虑。
这里我们给出第三种解题思路:有序数组的中位数实际上就是数组中的第len/2个数(偶数的话就是两个数的均值)。因此找中位数可以转化为求数组中第k小的数字。我们只要知道如何求第k小的数,那么对于长度为奇数的,我们直接找到第len/2+1小的数字就是中位数,而偶数的话,就找到第len/2小和第len/2+1小的数字取均值。
因此,我们的问题就转化为如何在两个有序数组中找第k小的数字。
这里有一个比较好的方法:为了找第k小的数字,我们比较两个数组中第k/2个数字,也就是将nums1[k/2-1]和nums2[k/2-1]进行比较,如果哪个小,那么它以及它之前的数字都不会是第k小的数字,可以排除,在剩余的数据里面重复这个过程进行查找。
实际上这个道理并不难理解:如下图所示,如果nums1[k/2-1]小于nums2[k/2-1],那么首先它之前的数都是小于nums1[k/2-1],假设nums2数组中nums2[k/2-1]前面的数也都小于它(实际上不一定都小于),那么所有比nums1[k/2-1]小的数最多一共有k/2-1+k/2-1个,即k-2个,也就是说nums1[k/2-1]最多可能是第k-1小,不可能是第k小,因此,它和它之前的数字都可以排除掉。
反之,如果nums1[k/2-1]大于nums2[k/2-1],就可以排除掉nums2[k/2-1]及它之前的数,如果这两个数相等,那么实际上任选一个数组进行排除就可以了,仍然是排除掉k/2个数。
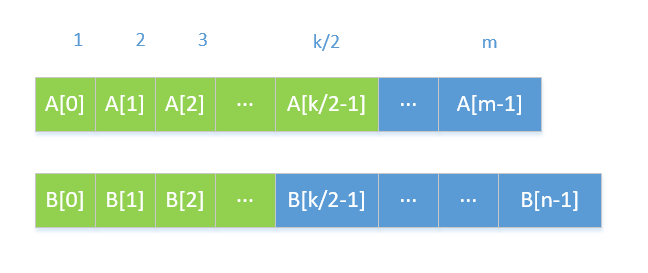
因此,我们的第三种解法就是:每次都取k的一半处的元素进行比较,相对小的那个数组中k/2及其之前的元素都可以排除掉,然后继续在剩余数组找第k小元素(注意:由于已经排除了k/2个元素,所以k的值要减去排除掉的元素个数)。
很明显,这是一个重复的过程,因此可以通过递归来进行解决,这里要注意递归的终止条件和数组的越界问题,k/2要和数组长度进行比较,取其较小值。另外,由于每次去掉k/2个元素,因此最后一定是有一个数组变为了空,或者k会变为1,这就是终止条件,具体见如下所示的代码。
最后我们来分析这个解法的复杂度,解法三我们每一次循环排除掉k/2个元素,所以时间复杂度是O(logk),而k是m+n的一半,所以时间复杂度为O(log(m+n)),没有用到额外空间,空间复杂度为O(1)。
class Solution {
//解法三:相当于求两个有序数组的第k小数字
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m = nums1==null?0:nums1.length;
int n = nums2==null?0:nums2.length;
int len=m+n;
if(len%2==0) //偶数
return (findKthNum(nums1,nums2,0,0,len/2) + findKthNum(nums1,nums2,0,0,len/2 + 1)) / 2.0;
else
return findKthNum(nums1,nums2,0,0,len/2+1);
}
//找第k小数字,i和j表示两个数组的起始位置
public int findKthNum(int[] nums1,int[] nums2,int i,int j,int k){
int m=nums1.length;
int n=nums2.length;
if(i>=m) //nums1空
return nums2[j+k-1];
if(j>=n) //nums2空
return nums1[i+k-1];
if(k==1)
return Math.min(nums1[i],nums2[j]);
int index=k/2-1;
int nums1Index=Math.min(m-1,i+index);
int nums2Index=Math.min(n-1,j+index);
if(nums1[nums1Index]<nums2[nums2Index])
return findKthNum(nums1,nums2,nums1Index+1,j,k-(nums1Index-i+1));
else
return findKthNum(nums1,nums2,i,nums2Index+1,k-(nums2Index-j+1));
}
}
解法四:数据流的中位数
如果做过《剑指Offer》上相关的习题,我们应该记得也有一道关于中位数的题目,可以参考:【剑指Offer】63、数据流中的中位数。在该题中,由于数据是从数据流中逐一读出,因此我们选用了适当的数据结构对其进行保存,由于中位数的性质,我们最好的数据结构是选用了最大堆和最小堆,用一个最大堆实现左边的数据存储,用一个最小堆实现右边的数据存储,并保证数据平均分到两个堆中,所有最大堆的数据都小于最小堆的数据,此时我们说堆顶的数据就是中位数。
受该题的启发,我们当然也可以把这两个数组的数据看作一个数据流,依次加入到最大堆和最小堆中,进而就可以利用该题的算法得到求解。这样时间复杂度仍然为O(log(m+n)),但是使用了两个堆的额外空间。
本解法的实现参考:【剑指Offer】63、数据流中的中位数
解法五:切分法,左边最大小于右边最小
从解法四出发,我们考虑能不能不使用额外的空间,在数组中达到同样的效果,这就是在LeetCode中给出的本题的题解算法。
如果我们将一个数组切分为两半,一个长度为 m 的数组,有 0 到 m 总共 m + 1 个位置可以切,假设数组A在位置i处切,数组B在位置j处切,然后将i的左边和j的左边合成左半部分,i的右边和j的右边合成右半部分。然后类似于解法四,如果我们能保证(1)所有数据平均分到两边;(2)左边的元素都小于右边的元素;那么中位数就只跟左边的最大值和右边的最小值相关(相当于解法四种的堆顶)。

要满足以上两个条件,关键就在于如何确定i和j的位置,我们分情况来考虑:
(1)如果m+n是偶数,那么左右两边的数据个数应该是相等的,并且中位数就是(左半部分最大值 + 右半部分最小值 )/ 2 。此时,根据上图我们可以知道左边数据长度等于右边数据长度,即i+j=m-i+n-j,所以j=(m+n)/2-i。
(2)如果m+n是奇数,那么左半部分的长度比右半部分大 1 ,并且中位数就是左半部分的最大值。此时,有:左边的数据长度=右边的数据长度+1,即i+j = m-i + n-j + 1,所以j=(m+n+1)/2-i。
由于当m+n是偶数时,(m+n)/2和(m+n+1)/2是一样的,所以上述两种情况可以合并,也就是说只需要确定i的位置,我们就可以得到j的位置,即满足j=(m+n+1)/2-i。
上述i和j的关系我们是基于第一个条件进行考虑的,接下来考虑第二个条件,要想让左边的元素都小于右边的元素,只要让左边的最大值小于右边的最小值即可。由于数组有序,那么左边的最大值一定只有两种情况,即要么是A[i-1],要么是B[j-1],右边的最小值也一定只有两种情况,要么是A[i],要么是B[j],同样分两种情况:
(1)如果左边A[i-1]最大,那么它一定小于A[i],只需和B[j]进行比较,如果也小于B[j],那么就满足了第二条件;如果大于B[j],此时应该减小i,增大j(因为如果i更大,j更小,那么A[i-1]只会比B[j]更大。
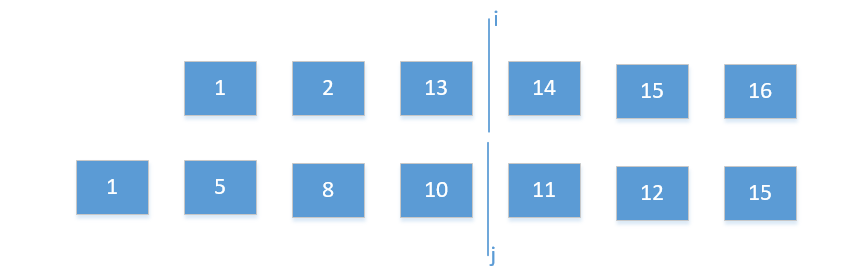
(2)如果左边B[j-1]最大,那么它一定小于B[j],只需和A[i]进行比较,如果也小于A[i],那么就满足了第二条件;如果大于A[i],此时应该增大i,减小j(因为如果i更小,j更大,那么B[j-1]只会比A[i]更大。
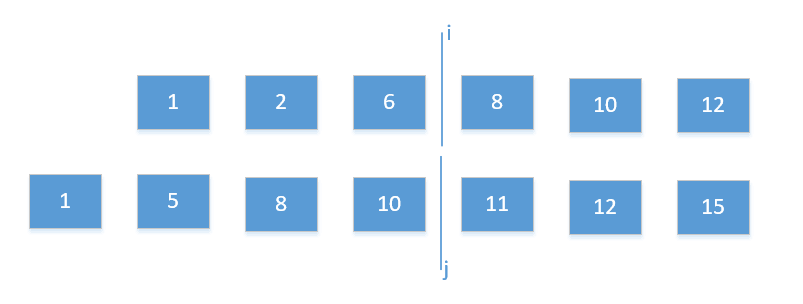
分析到这里,我们应该就知道如何去找合适的i的位置,我们可以通过二分的方法去查找,然后通过上述两种情况的比较增大或者减小i的范围,进而找到合适的i的位置,并通过j的公式求出j,这样我们就可以很容易的找到中位数。
注意:这里还有一个问题就是:由于 0 <= i <= m ,为了保证 0 <= j <= n ,我们必须保证 m <= n ,因此我们每次都是对较短的那个数组进行切分。
因此,我们可以看到此解法和数据流中位数基于堆的解法实际上有异曲同工之妙,只不过数据结构不同。由于是对较短的数组进行二分,因此此算法的时间复杂度为O(log(min(m,n))).
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
//解法4:切分法,左边最大小于右边最小
int m = nums1==null?0:nums1.length;
int n = nums2==null?0:nums2.length;
if(m>n) //保证m是小于n的
return findMedianSortedArrays(nums2,nums1);
//通过二分查找,在较短的那个数组里找一个位置i,使得左边最大小于右边最小
int low=0,high=m;
while(low<=high){
int i=(low+high)/2;
int j=(m+n+1)/2-i;
if(j!=0 && i!=m && nums1[i] < nums2[j-1]) //此时应该增大i
low=i+1;
else if(i!=0 && j!=n && nums1[i-1]> nums2[j]) //此时应该减小i
high=i-1;
else{ //此时i符合条件,找到了i
//找到左边最大的
int maxLeft=0;
if(i==0)
maxLeft=nums2[j-1];
else if(j==0)
maxLeft=nums1[i-1];
else
maxLeft=Math.max(nums1[i-1],nums2[j-1]);
if((m+n)%2!=0) //奇数,左边最大的就是中位数
return maxLeft;
//找到右边最小的
int minRight=0;
if(i==m)
minRight=nums2[j];
else if(j==n)
minRight=nums1[i];
else
minRight=Math.min(nums1[i],nums2[j]);
return (maxLeft+minRight)/2.0;
}
}
return 0.0;
}
总结
作为第一道hard级别的题目,此题确实是有一定难度的,我们给出的五种解法中,时间复杂度逐步降低,最重要的是这里体会到二分查找的灵活运用,建议先看一下剑指Offer:数据流的中位数那道题目,对比这里的解法四和解法五可以比较容易理解。