1. 正态分布
1.1. wiki
1.2. 生成正态高斯正态分布随机数
来源:http://www.cnblogs.com/yeahgis/archive/2012/07/13/2590485.html
#include <stdlib.h>
#include <math.h>
double gaussrand()
{
static double V1, V2, S;
static int phase = 0;
double X;
if ( phase == 0 ) {
do {
double U1 = (double)rand() / RAND_MAX;
double U2 = (double)rand() / RAND_MAX;
V1 = 2 * U1 - 1;
V2 = 2 * U2 - 1;
S = V1 * V1 + V2 * V2;
} while(S >= 1 || S == 0);
X = V1 * sqrt(-2 * log(S) / S);
} else
X = V2 * sqrt(-2 * log(S) / S);
phase = 1 - phase;
return X;
}
这样生成的高斯分布随机数序列的期望为0.0,方差为1.0。若指定期望为E,方差为V,则只需增加:
期望 :
方差 :
1.3. 计算概率密度函数CDF Φ(x)
1.3.1. 方法1
参考链接:Stand-alone C++ implementation of Φ(x)
The function Φ(x) is the cumulative density function (CDF) of a standard normal (Gaussian) random variable. It is closely related to the error function erf(x).
#include <cmath>
double phi(double x)
{
// constants
double a1 = 0.254829592;
double a2 = -0.284496736;
double a3 = 1.421413741;
double a4 = -1.453152027;
double a5 = 1.061405429;
double p = 0.3275911;
// Save the sign of x
int sign = 1;
if (x < 0)
sign = -1;
x = fabs(x)/sqrt(2.0);
// A&S formula 7.1.26
double t = 1.0/(1.0 + p*x);
double y = 1.0 - (((((a5*t + a4)*t) + a3)*t + a2)*t + a1)*t*exp(-x*x);
return 0.5*(1.0 + sign*y);
}
void testPhi()
{
// Select a few input values
double x[] =
{
-3,
-1,
0.0,
0.5,
2.1
};
// Output computed by Mathematica
// y = Phi[x]
double y[] =
{
0.00134989803163,
0.158655253931,
0.5,
0.691462461274,
0.982135579437
};
int numTests = sizeof(x)/sizeof(double);
double maxError = 0.0;
for (int i = 0; i < numTests; ++i)
{
double error = fabs(y[i] - phi(x[i]));
if (error > maxError)
maxError = error;
}
std::cout << "Maximum error: " << maxError << "
";
}
1.3.2. 方法2-NVIDIA
参考原链接:c/c++/c# 快速计算 Cumulative Normal Distribution 正态累积函数CDF
static double CND(double d)
{
const double A1 = 0.31938153;
const double A2 = -0.356563782;
const double A3 = 1.781477937;
const double A4 = -1.821255978;
const double A5 = 1.330274429;
const double RSQRT2PI = 0.39894228040143267793994605993438;
double
K = 1.0 / (1.0 + 0.2316419 * fabs(d));
double
cnd = RSQRT2PI * exp(- 0.5 * d * d) *
(K * (A1 + K * (A2 + K * (A3 + K * (A4 + K * A5)))));
if (d > 0)
cnd = 1.0 - cnd;
return cnd;
}
1.3.3. 方法3 内插法
像查表那样,预先计算一部分值,然后内插,为保证精度能达到要求,预选值有一定的选择条件。
参考
1.4. 误差函数erf(x)
根据选择方法的不同有不同的计算代码
其中一个来源于这里
Here’s a Python implementation of erf(x) based on formula 7.1.26 from A&S. The maximum error is below 1.5 × 10-7.
import math
def erf(x):
# constants
a1 = 0.254829592
a2 = -0.284496736
a3 = 1.421413741
a4 = -1.453152027
a5 = 1.061405429
p = 0.3275911
# Save the sign of x
sign = 1
if x < 0:
sign = -1
x = abs(x)
# A & S 7.1.26
t = 1.0/(1.0 + p*x)
y = 1.0 - (((((a5*t + a4)*t) + a3)*t + a2)*t + a1)*t*math.exp(-x*x)
return sign*y
This problem is typical in two ways: A&S has a solution, and you’ve got to know a little background before you can use it.The formula given in A&S is only good for x ≥ 0. That’s no problem if you know that the error function is an odd function, i.e. erf(-x) = -erf(x). But if you’re an engineer who has never heard of the error function but needs to use it, it may take a while to figure out how to handle negative inputs.One other thing that someone just picking up A&S might not know is the best way to evaluate polynomials. The formula appears as 1 – (a1t1 + a2t2 + a3t3 + a4t4 + a5t5)exp(-x2), which is absolutely correct. But directly evaluating an nth order polynomial takes O(n2) operations, while the factorization used in the code above uses O(n) operations. This technique is known as Horner’s method.
1.5. 卡方检验
参考wiki卡方分布
1.5.1. 概率密度函数
卡方分布(Chi-squared Distribution)Chi-squared distribution
(
1.5.1.1. 代码1
double PChisquared(double b, int x)
{
double f = 0;
if (x < 0) f = 0;
else
{
f = (pow(b, x / 2 - 1)*exp(-b / 2)) / (power(2, x / 2)*tgamma(x / 2));
}
return f;
}
1.5.1.2. 代码2
double CND(double d)
{
const double A1 = 0.31938153;
const double A2 = -0.356563782;
const double A3 = 1.781477937;
const double A4 = -1.821255978;
const double A5 = 1.330274429;
const double RSQRT2PI = 0.39894228040143267793994605993438;
double
K = 1.0 / (1.0 + 0.2316419 * fabs(d));
double cnd = RSQRT2PI * exp(-0.5 * d * d) *(K * (A1 + K * (A2 + K * (A3 + K * (A4 + K * A5)))));
if (d > 0)
cnd = 1.0 - cnd;
return cnd;
1.5.1.3. 代码3
//c/c++/c# 快速计算 Cumulative Normal Distribution 正态累积函数CDF 此函数版权属于NVIDIA
/*方法2 https://www.johndcook.com/blog/cpp_phi/*/
double phi(double x)
{
// constants
double a1 = 0.254829592;
double a2 = -0.284496736;
double a3 = 1.421413741;
double a4 = -1.453152027;
double a5 = 1.061405429;
double p = 0.3275911;
// Save the sign of x
int sign = 1;
if (x < 0)
sign = -1;
x = fabs(x) / sqrt(2.0);
// A&S formula 7.1.26
double t = 1.0 / (1.0 + p * x);
double y = 1.0 - (((((a5*t + a4)*t) + a3)*t + a2)*t + a1)*t*exp(-x * x);
return 0.5*(1.0 + sign * y);
}
1.5.2. 概率值CDF(累积分布函数)
(gamma(s,t))表示下不完全Γ函数,定义为:
对应的上不完整(Gamma)函数为:
上不完整和下不完整函数之和等于gamma函数的和。即:
(=lim limits_{x o infty} gamma(s,t))
C语言中其实自带上述不完整函数概率函数。参考这里.
tgamma(a,z) gamma函数上无穷
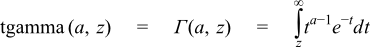
tgamma_lower(a,z) gamma