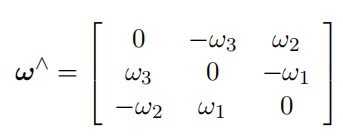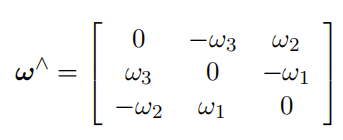手写VIO（一）概论与预备知识

第一章 VIO概论

当前市面上很少有系统介绍VIO系统的书

一 VIO简介

VIO（Visual-Inertial Odometry）：以视觉和IMU融合的方法实现定位的里程计

接下来介绍VIO使用到的两个信息

1. IMU（Inertial MeasureMent Unit）惯性测量单元

典型的6轴IMU能以较高频率（>= 100Hz）返回被测量物体的角速度和加速度
IMU的缺点在于，容易收到自身温度、灵片、振动等因素干扰，通过积分直接得到的评议和旋转将产生漂移

2. 视觉信息

通过视觉定位的方法即视觉SLAM，主要利用相机采集的图片信息作为输入，采样频率较低（15-60Hz居多）
定位的时候主要通过图像特征点或像素推断相机运动

之所以使用以上两个硬件主要是由于二者的互补性。

3. 二者的互补性

IMU与视觉定位的优劣势对比

方案	IMU	视觉
优势	快速响应不受成像质量影响角速度普遍比较准确可估计绝对尺度	不产生漂移直接测量旋转与平移
劣势	存在零偏低精度IMU积分位子发散高精度IMU价格昂贵	受图像遮挡、运动物体干扰单目视觉无法测量尺度单目纯旋转运动无法估计快速运动时易丢失

可以看出视觉与IMU之间存在一定的互补性质：

IMU适合于计算短时间快速的运动
视觉适合计算长时间慢速的运动

同时，可以利用视觉定位信息来估计好吃IMU的零偏，减少IMU由零偏导致的发散和累积误差。

反之，IMU也可以为视觉提供快速运动的定位。

应用

IMU数据可以多种定位方案融合

自动驾驶中通常使用IMU+GPS差分GPS/RTK的融合定位方案，形成GNSS-INS组合导航系统，打倒厘米组定位精度；
头戴式AR/VR头盔则多使用视觉+IMU的VIO定位系统，形成高帧率定位方案

里程计的后端

根据信息融合的方式进行分类我们可以把视觉里程计分为松耦合和紧耦合两种

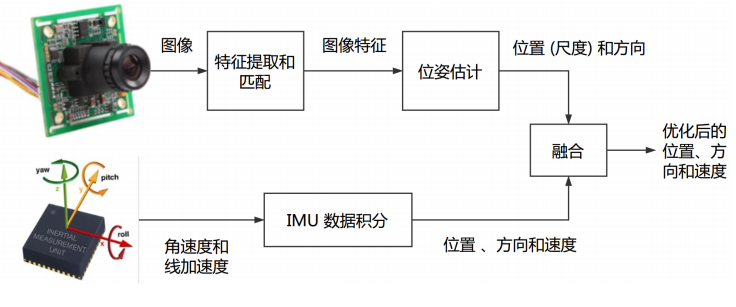
松耦合

将 IMU 定位与视觉/GNSS 的位姿直接进行融合，融合过程对二者本身不产生影响，作为后处理方式输出。典型方案为卡尔曼滤波器。

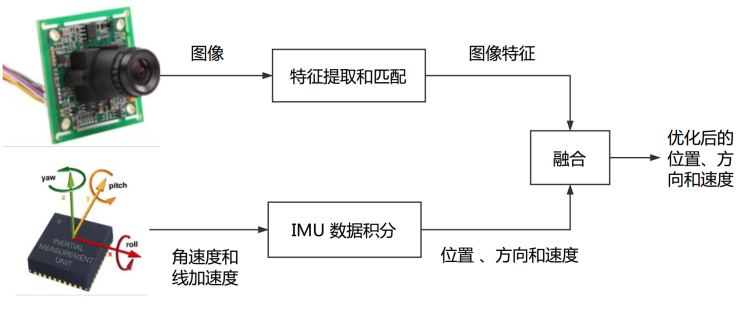
紧耦合

融合过程本身会影响视觉和 IMU 中的参数（如 IMU 的零偏和视觉的尺度）。典型方案为 MSCKF 和非线性优化。

为什么要使用紧耦合？

单纯凭（单目）视觉或 IMU 都不具备估计 Pose 的能力：视觉存在尺度不确定性、IMU 存在零偏导致漂移；
松耦合中，视觉内部 BA 没有 IMU 的信息，在整体层面来看不是最优的。
紧耦合可以一次性建模所有的运动和测量信息，更容易达到最优。

二预备知识

2.1 三维刚体运动的表示

首先需要在机器人/车辆上定义各种坐标系，如：

世界坐标系 W；
IMU坐标系 I；
相机坐标系 C；

坐标系之间的变换关系由一个SE(3)给出。如I到W系的变换矩阵：(T_{W_i})

[T_{W_i} = left[ egin{array}{ccc} R_{WI}&t_{WI}\ 0^{T}&1 end{array} ight] in R^{4 imes 4} ]

(R_{WI})为(3 imes 3)的旋转矩阵，(t_{WI})为平移向量。

(T_{WI})右乘一个I系下（其次）坐标，将得到该点W系下坐标。

通常默认有以下约定：

当某个量表达坐标系的转换关系，写在右下脚标，例如(T_{WB})。
当表达矢量在某坐标系中取的坐标时，写在右上角标，如(v^{omega})表达速度矢量在World系坐标
IMU坐标系即I系也称为Body系。
定义明确时，有时会省略该脚标，我们会直接谈论R,t这样的量
不刻意区分齐次和非齐次坐标，因为在程序中可以自动完成转换，且无歧义
默认以 (T_{WI}) 表达并存储 IMU 的定位信息，而不是 (T_{IW}) 。二者实际互为逆，存储哪一类区别不大，视习惯而定。
同理，(T_{WI}) 的平移部分可直接视作 IMU 在世界中的坐标，从而进行绘图或可视化操作。

四元数

旋转矩阵 R 亦可用四元数 q 描述。

四元数 q 有一个实部和三个虚部。我们把实部写在前：(q = [q0, q1, q2, q3]^⊤) 或 (q = [w, x, y, z]^⊤)

其中 (q_0) 为实部，([q_1, q_2, q_3]^⊤) 为虚部。因为实部为标量，虚部为矢量，所以也可记为：

[q = [s, v]^⊤ ]
其中 s 为标量，v 为虚部的矢量。

四元数乘法

此外，四元数可类似复数，定义加减、模长、逆、共轭等运算，不一一展开。

角速度：

[omega = lim_{Delta arr 0}frac{partial heta}{Delta t} ]

四元数的导数

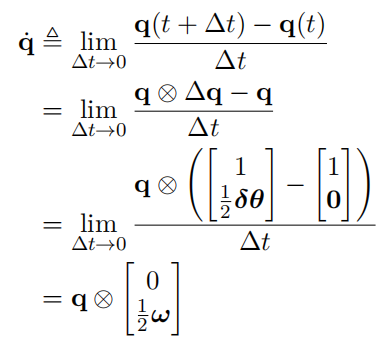
李代数

除了利用四元数求导，亦可利用李代数进行旋转求导。使用旋转矩阵 R 时，角速度为 ω，那么 R 相对于时间的导数可写作：

[dot {R} = Rω ]

该式被称为泊松公式（Possion’s equation），其中 ∧ 为反对称矩阵算子：

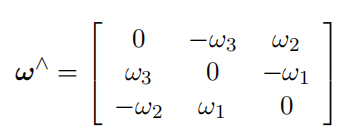
在本课程中亦记作：(ω_×) 或者 ([ω]_×)，表达含义相同。

so(3) 导数

在优化带有旋转的函数时，通常计算一个增量 ϕ ∈ so(3)，然后用它更新当前估计值：

[R ← R exp(ϕ^∧) ]

其中 exp 为 so(3) 至 SO(3) 上的指数映射。
本课程习惯为右乘，实际当中左右乘等价，仅为习惯上的差别。
注：(i) 不同的 R 函数，具体的导数形式也不同。(ii) 在程序中，不必区分 R 是以矩阵存储或是以四元数存储，只需按照该式更新即可。

2.2 重要的雅克比求导

常见的一些雅可比（以自变量为 R 举例）：

1. 旋转点的左扰动雅可比：

（中间的变换可以考虑向量的叉乘形式）。

2. 旋转点的右扰动雅克比

3. 旋转连乘的雅克比：

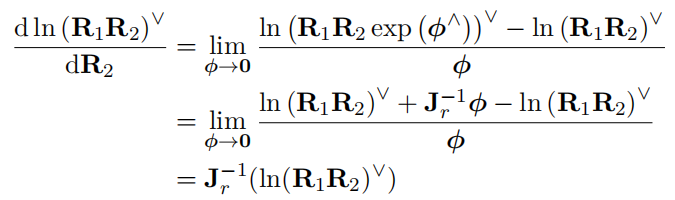
其中用到了对(R):

[ln(Rexp(phi^{wedge}))^{vee} = ln(R)^{vee}+J^{-1}_rphi ]

和(J_r^{-1})为SO3上的右雅克比：

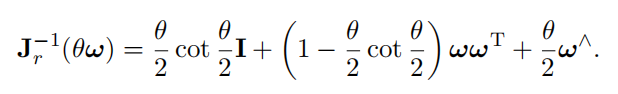
4. 旋转连乘的雅克比：

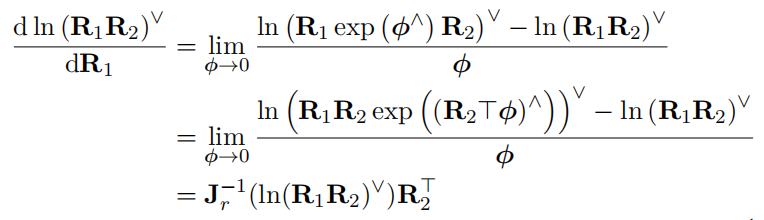
这里用到了SO(3)的伴随性质：

有关 SE(3)：由于 SE(3) 李代数性质复杂，在 VIO 中，我们通常使用SO(3) + t 的形式表达旋转和平移。对平移部分使用矢量更新而非SE(3) 上的更新。

三后续作业

3.1 VIO 文献阅读

阅读VIO 相关综述文献如a，回答以下问题：

1. 视觉与IMU 进行融合之后有何优势？

答：

视觉定位的优点在于不会产生漂移，可以直接测量旋转和平移；缺点在于当存在外界图像遮挡、且运动物体干扰时影响较大，定位不准；当使用单目视觉进行测量时还存在尺度不确定性的问题，而且单目视觉定位无法估计纯旋转运动；当相机快速运动时定位容易丢失。

IMU的优点在于输出频率高（100hz以上）能够快速响应，受外界影响小（不受成像质量影响），角速度普遍比较准确，并且可估计绝对尺度；缺点在于IMU受温度影响，存在零偏；并且使用低精度IMU得到积分容易发散，长时间跟踪容易产生累积漂移。而高精度的IMU价格比较昂贵。

2. 有哪些常见的视觉+IMU 融合方案？有没有工业界应用的例子？

常见的视觉+IMU融合方案包括：

VINS-mono及各种改进（VINS_Fusion）
MSCKF (基于KF滤波器实现)
OKVIS
ROVIO
VIORB
ICE-BA(百度)

工业界应用的例子包括AR Core。虚拟现实领域中AR Kit 通过VIO实现移动设备在空间中的精确定位。在虚拟现实头显中的Inside-out 定位中，目前被广泛采用的方案就是视觉惯性传感器融合实现 SLAM的 VINS 算法。

3.在学术界，VIO 研究有哪些新进展？有没有将学习方法用到VIO中的例子？你也可以对自己感兴趣的方向进行文献调研，阐述你的观点

目前的学术界中，VIO提高的主要方向包括精度、鲁棒性、效率三部分；

在VIO中，可以深度学习网络来预测相机的位姿状态、场景深度等。还可以使用深度网络剔除动态物体等以提高VIO系统的鲁棒性。

利用了深度学习的例子包括有D3VO（使用深度学习来预测场景深度、光度、姿态等），VINet（使用深度网络来预测相机位姿）DeepVO（使用网络来预测位姿）等；

3.2 四元数和李代数更新

课件提到了可以使用四元数或旋转矩阵存储旋转变量。当我们用计算出来的对某旋转更新时，有两种不同方式：

[Rleftarrow Rexp(omega^wedge) ]

或

[qleftarrow qotimes[1,frac{1}{2}omega]^T ]

请编程验证对于小量(omega = [0.01, 0.02, 0.03]^T)，两种方法得到的结果非常接近，实践当中可视为等同。因此，在后文提到旋转时，我们并不刻意区分旋转本身是q 还是R，也不区分其更新方式为上式的哪一种。

答：

编程过程包括如下步骤：

生成初始的四元数和随机矩阵
利用小量生成旋转角和旋转轴，得到对应的旋转矩阵和四元数
更新四元数和旋转矩阵
计算差值

部分源代码如下：

int main()
{
    Vector3d w(0.01,0.02,0.03); //旋转向量 可以理解为角速度
    //生成一个随机的旋转矩阵
    Vector3d v = Vector3d::Random();
    v.normalize();
    // Matrix3d R = Eigen::Matrix3d::Random();
    Matrix3d R = Eigen::AngleAxisd(M_PI/4,v).toRotationMatrix();
    Quaterniond q(R);
    cout<<"初始四元数:"<< endl <<q.coeffs().transpose()<<endl;
    cout<<"初始旋转矩阵:"<< endl <<R<<endl;

    //获得旋转向量对应的旋转角
    double theta = w.norm(); //旋转对应的旋转角
    Vector3d n_w = w/theta; //归一化得到旋转角得到的旋转轴
    //利用旋转角更新旋转矩阵
    Matrix3d DeltaR = AngleAxisd(theta,n_w).toRotationMatrix();
    Matrix3d R_update = R*DeltaR;
    cout<<"更新后的旋转矩阵："<<endl<<R_update<<endl;
    
    //利用小量更新四元数
    Quaterniond deltaq(1,w(0)/2,w(1)/2,w(2)/2);
    Quaterniond q_update = q*deltaq;
    //更新之后对四元数进行归一化
    //q_update = q_update.normalized(); //1
    q_update.normalize();
    cout<<"更新后的四元数:"<<endl<<q_update.coeffs().transpose()<<endl;

    cout<<"两种方法得到的结果之差："<<endl;    
    cout<<q_update.toRotationMatrix()-R_update<<endl;

    return 0;
}

生成结果如图所示：

可以看出最后结果的差值在小数点后六位，因此两种方法效果类似。

3.3 其他导数推导

使用右乘(so(3))，推导一下导数：

[frac{d R^{-1}p}{d R}\ frac{d ln(R_1R_2^{-1})^{wedge}}{dR_2} ]

答：推导过程如下：

[egin{aligned} frac{partial R^{-1}p}{partial R}&=lim_{phi arr 0} frac{{(Rexp(phi)^{wedge})}^{-1}p-R^{-1} p }{phi} \&=lim_{phi arr 0}frac{{(exp(phi^{wedge})^{-1}R^{-1}}p-R^{-1} p }{phi} \&=lim_{phi arr 0}frac{(exp(phi^{wedge})^{-1}-I)R^{-1}p}{phi} \&=lim_{phi arr 0}frac{((I+{phi^wedge})^{-1}-I)R^{-1}p}{phi} \&=lim_{phi arr 0}frac{((I-{phi^wedge})-I)R^{-1}p}{phi} \&=lim_{phi arr 0}frac{-{phi^wedge}R^{-1}p}{phi} \&=lim_{phi arr 0}frac{(R^{-1}p)^{wedge}phi}{phi} \&=(R^{-1}p)^{wedge} end{aligned} ]

用到的性质如下：

一：(R)、(exp(phi^{wedge}))和(Rexp(phi^{wedge}))都代表旋转矩阵，旋转矩阵的逆与转置相等，这里所有的逆都相当于转置，也就是用的矩阵转置的性质((Rexp(phi^{wedge}))^{-1} = exp(phi^{wedge})^{-1}R^{-1})(来自网络)
二：泰勒展开：(exp{varphi^{wedge}}approx I+varphi^{wedge})
三：反对称矩阵:((varphi^{wedge})^T = -varphi^{wedge})
四：《视觉-SLAM十四讲》P42,概括为如下公式：(a imes b=a^wedge b=-b imes a=-b imes a)。

[egin{aligned} frac{d ln(R_1R_2^{-1})^{vee}}{dR_2}&= lim_{varphi arr 0}frac{ln (R_1(R_2exp{(phi^{wedge})})^{-1})^{vee}-ln(R_1R_2^{-1})^{vee}}{varphi} \&= lim_{varphi arr 0}frac{ln(R_1(exp{phi^{wedge})}^{-1}R_2^{-1})^{vee}-ln(R_1R_2^{-1})^{vee}}{varphi} \&= lim_{varphi arr 0}frac{ln(R_1R_2^{-1}R_2(exp{phi^{wedge})}^{-1}R_2^{-1})^{vee}-ln(R_1R_2^{-1})^{vee}}{varphi} \&= lim_{varphi arr 0}frac{ln(R_1R_2^{-1}R_2(exp{phi^{wedge})}^{-1}R_2^{T})^{vee}-ln(R_1R_2^{-1})^{vee}}{varphi} \&= lim_{varphi arr 0}frac{ln(R_1R_2^{-1}(exp{(R_2phi)^{wedge})}^{-1})^{vee}-ln(R_1R_2^{-1})^{vee}}{varphi} \&= lim_{varphi arr 0}frac{ln(R_1R_2^{-1})^{vee}+J_r^{-1}(ln(R_1R_2^{-1})^{vee})(-R_2varphi)-ln(R_1R_2^{-1})^{vee}}{varphi} \&= -J_r^{-1}(ln(R_1R_2^{-1})^{vee})R_2 end{aligned} ]

重要的几个点

其中第三行第四行用到了伴随矩阵的性质（在SLAM第四讲中有学）

第四行到第五行使用了如下性质：

[ln(Rexp(varphi^{wedge}))^{vee} = ln R^{vee}+J^{-1}_r(ln R^{vee}) ]