适用范围:给定的图存在负权边,这时类似Dijkstra等算法便没有了用武之地,而Bellman-Ford算法的复杂度又过高,SPFA算法便 派上用场了。 我们约定有向加权图G不存在负权回路,即最短路径一定存在。当然,我们可以在执行该算法前做一次拓扑排序,以判断是否存在负权回路,但这不是我们讨论的重 点。
算法思想:我们用数组d记录每个结点的最短路径估计值,用邻接表来存储图G。我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的
结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在
当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止
期望的时间复杂度O(ke), 其中k为所有顶点进队的平均次数,可以证明k一般小于等于2。
实现方法:
建立一个队列,初始时队列里只有起始点,再建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为 0)。然后执行松弛操作,用队列里有的点作为起始点去刷新到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列 为空。
判断有无负环:
如果某个点进入队列的次数超过N次则存在负环(SPFA无法处理带负环的图)
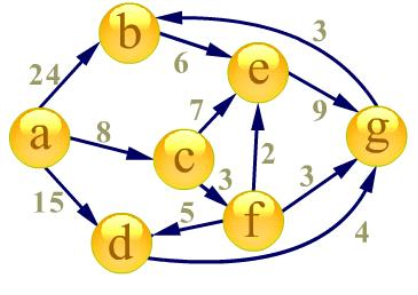
首先建立起始点a到其余各点的
最短路径表格
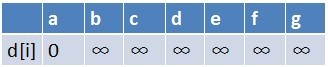
首先源点a入队,当队列非空时:
1、队首元素(a)出队,对以a为起始点的所有边的终点依次进行松弛操作(此处有b,c,d三个点),此时路径表格状态为:
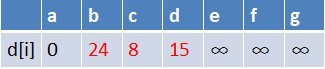
在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点
需要入队,此时,队列中新入队了三个结点b,c,d
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e点),此时路径表格状态为:
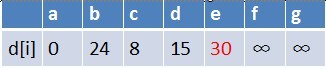
在最短路径表中,e的最短路径估值也变小了,e在队列中不存在,因此e也要
入队,此时队列中的元素为c,d,e
队首元素c点出队,对以c为起始点的所有边的终点依次进行松弛操作(此处有e,f两个点),此时路径表格状态为:
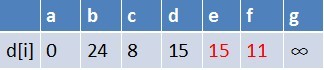
在最短路径表中,e,f的最短路径估值变小了,e在队列中存在,f不存在。因此
e不用入队了,f要入队,此时队列中的元素为d,e,f
队首元素d点出队,对以d为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
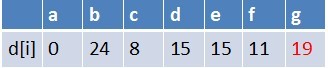
在最短路径表中,g的最短路径估值没有变小(松弛不成功),没有新结点入队,队列中元素为f,g
队首元素f点出队,对以f为起始点的所有边的终点依次进行松弛操作(此处有d,e,g三个点),此时路径表格状态为:

在最短路径表中,e,g的最短路径估值又变小,队列中无e点,e入队,队列中存在g这个点,g不用入队,此时队列中元素为g,e
队首元素g点出队,对以g为起始点的所有边的终点依次进行松弛操作(此处只有b点),此时路径表格状态为:
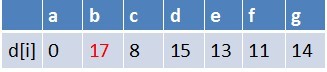
在最短路径表中,b的最短路径估值又变小,队列中无b点,b入队,此时队列中元素为e,b
队首元素e点出队,对以e为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
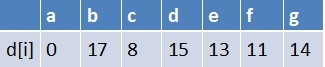
在最短路径表中,g的最短路径估值没变化(松弛不成功),此时队列中元素为b
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e这个点),此时路径表格状态为:

在最短路径表中,e的最短路径估值没变化(松弛不成功),此时队列为空了
最终a到g的最短路径为14
program:
#include<cstdio>
using namespace std;
struct node
{int x;
int value;
int next;
};
node e[60000];
int visited[1505],dis[1505],st[1505],queue[1000];
int main()
{
int n,m,u,v,w,start,h,r,cur;
freopen("c.in","r",stdin);
freopen("c.out","w",stdout);
while(scanf("%d%d",&n,&m)!=EOF)
{
for(int i=1;i<=1500;i++)
{visited[i]=0;
dis[i]=-1;
st[i]=-1; //这个初始化给下边那个while循环带来影响
}
for(int i=1;i<=m;i++)
{
scanf("%d%d%d
",&u,&v,&w);
e[i].x=v; //记录后继节点 相当于链表中的创建一个节点,并使得数据域先记录
e[i].value=w;
e[i].next=st[u]; //记录顶点节点的某一个边表节点的下标,相当于在链表中吧该边表节点的next指针先指向他的后继边表节点
st[u]=i; //把该顶点的指针指向边表节点,相当于链表中的插入中,头结点的指针改变
}
start=1;
visited[start]=1;
dis[start]=0;
h=0;
r=1;
queue[r]=start;
while(h!=r)
{
h=(h+1)%1000;
cur=queue[h];
int tmp=st[cur];
visited[cur]=0;
while(tmp!=-1)
{
if (dis[e[tmp].x]<dis[cur]+e[tmp].value) //改成大于号才对
{
dis[e[tmp].x]=dis[cur]+e[tmp].value;
if(visited[e[tmp].x]==0)
{
visited[e[tmp].x]=1;
r=(r+1)%1000;
queue[r]=e[tmp].x;
}
}
tmp=e[tmp].next;
}
}
printf("%d
",dis[n]);
}
return 0;
}