二次剩余学习小记（+斐波那契通项公式推导）

斐波那契通项公式

来自https://www.zhihu.com/question/25217301/answer/158753864

(F(x)=x+x^2+2x^3+3x^4+4x^5+...=frac{x}{1-x-x^2})

设(F(x)=frac{a}{1-cx}+frac{b}{1-dx})，可以列出方程

根据③④可以解得

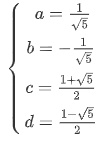
那么把(F(x))展开可得

(F(x)=sum (ac^i+bd^i)x^i)

(F_n=ac^n+bd^n=frac{1}{sqrt5}[(frac{1+sqrt5}{2})^n-(frac{1-sqrt5}{2})^n])

群论

基础定义：

https://www.cnblogs.com/nosta/p/9444576.html

https://blog.csdn.net/Fredric_2014/article/details/84251441

https://wenwen.sogou.com/z/q736604849.htm

https://zhidao.baidu.com/question/92977832.html

https://en.wikipedia.org/wiki/Field_(mathematics)

https://en.wikipedia.org/wiki/Algebraic_number_field

将就看一下吧（

一个域大概就是一个集合加上运算符，满足交换律集合率分配律逆元之类的，操作后的元素一定在范围内

~~并不知道学了一天学了什么东西~~

二次剩余

判断

求(x^2equiv n(mod;p))的一组解，即对n开根

定义勒让德符号((frac{n}{p})=n^{frac{p-1}{2}}(mod;p))，特判掉p|n

结论：((frac{n}{q})=1)是二次剩余，(=-1)不是二次剩余

证明：

首先由于(n^{p-1}equiv 1)，所以(n^{frac{p-1}{2}}equiv 1;or;-1)

①当n是二次剩余时

那么(sqrt n=n^{frac{1}{2}})有值，则(n^{frac{p-1}{2}}equiv 1)

②当n不是二次剩余时

((p-1)!)除掉1和p-1之后可以两两配对都为1（除掉1和-1之后逆元不等于自己，p^2-1=0）

所以((frac{n}{p})=-1)

计算

首先随机一个(a)使得(w=a^2-n,(frac{w}{p})=-1)，由于一个平方对应两个解所以只有一半的数是/不是二次剩余，因此期望次数为2

~~因为ω太难写了所以就用w代替~~

定义域(F_p=({0,1,...,p-1}))，里面有四则运算，除就是乘以逆元

定义扩域(F_{p2}={a+bsqrt w:x,yin F_p})，同样满足四则运算（类似虚数的操作），a和b都是模p意义下的整数（Fp里的）

证明一下逆元，即求（ω即√w）

解得

那么证得(F_{p2})是一个域

答案即为((a+sqrt w)^{frac{p+1}{2}})在(F_{p2})下的实数部分，另一个解显然是-x

证明（以下操作均在(F_{p2})中进行）：

(x=(a+sqrt w)^{frac{p+1}{2}},x^2=(a+sqrt w)^{p+1})

(=(a+sqrt w)^p(a+sqrt w))

二项式展开，根据lucas定理可以提出来一个C(0,>0)的组合数，所以组合数为0

（至于为什么可以模掉，正常来说没有整数乘实数再取模的操作，但这是在扩域下的运算所以可以）

(=(a^p+sqrt w^p)(a+sqrt w))

(=(a+sqrt w^{p-1}sqrt w)(a+sqrt w))

(=(a+(frac{w}{p})sqrt w)(a+sqrt w))

(=(a-sqrt w)(a+sqrt w))

(=a^2-(a^a-n))

(=n)

证毕，得到的是在(F_{p2})域下的解

根据拉格朗日定理（数论中的，不是群论的神仙东西），任意非0n次多项式在任何域下只有最多n个解，而(x^2equiv n(mod;p))在(F_p)中有2个解，在(F_{p2})中显然也是这2个解，所以((a+sqrt w)^{frac{p+1}{2}})没有虚数部分，实数部分就是答案

那么就做完了，时间复杂度O(log)

例题

http://acm.hdu.edu.cn/showproblem.php?pid=6755

强行二合一

模10^9+9意义下5是二次剩余

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define C(n,m) (jc[n]*Jc[m]%1000000009*Jc[(n)-(m)]%1000000009)
#define mod 1000000009
#define Mod 1000000007
#define two 500000005
#define ll long long
#define N 5
//#define file
using namespace std;

ll jc[100001],Jc[100001],w[100001],S1[100001],S2[100001],W,n,c,ans,five,s1,s2,s;
int T,K,i,j,k,l;
struct type{ll x,y;};
type operator + (type a,type b) {return {(a.x+b.x)%mod,(a.y+b.y)%mod};}
type operator - (type a,type b) {return {(a.x-b.x)%mod,(a.y-b.y)%mod};}
type operator * (type a,type b) {return {(a.x*b.x+a.y*b.y%mod*W)%mod,(a.x*b.y+a.y*b.x)%mod};}

ll qpower(ll a,ll b) {ll ans=1; while (b) {if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;} return ans;}
ll random(int x,int y) {return (1ll*rand()*233333+rand())%(y-x+1)+x;}
ll ldr(int t) {return qpower(t,(mod-1)/2);}
void work()
{
	static type A,B;
	ll a;
	do{
	a=random(0,mod-1);W=((a*a-N)%mod+mod)%mod;
	} while (ldr(W)==1);
	
	A={1,0},B={a,1};
	i=(mod+1)/2;
	while (i)
	{
		if (i&1) A=A*B;
		B=B*B;i>>=1;
	}
	five=A.x;
}
ll js(ll p) {if (p==1) return (n+1)%mod; return (qpower(p,(n+1)%(mod-1))-1)*(qpower(p-1,Mod))%mod;}

int main()
{
	#ifdef file
	freopen("hdu6755.in","r",stdin);
	#endif
	
	srand(time(NULL));
	work();
	jc[0]=jc[1]=Jc[0]=Jc[1]=w[1]=1;
	fo(i,2,100000) w[i]=mod-w[mod%i]*(mod/i)%mod,jc[i]=jc[i-1]*i%mod,Jc[i]=Jc[i-1]*w[i]%mod;
	
	scanf("%d",&T);
	for (;T;--T)
	{
		scanf("%lld%lld%d",&n,&c,&K);ans=0;
		s1=(1ll+five)*two%mod,s2=(1ll-five)*two%mod;
		s1=qpower(s1,c%(mod-1)),s2=qpower(s2,c%(mod-1));
		S1[0]=S2[0]=1;
		fo(i,1,K) S1[i]=S1[i-1]*s1%mod,S2[i]=S2[i-1]*s2%mod;
		fo(i,0,K)
		{
			s=S1[i]*S2[K-i]%mod;
			ans=(ans+js(s)*C(K,i)*(((K-i)&1)?-1:1))%mod;
		}
		printf("%lld
",(ans+mod)%mod*qpower(five,(mod-1)-K)%mod);
	}
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}