1001.Yes, Prime Minister
题意:1e6组数据,每次给定xi,求长度最短的一个包含xi的区间[l,r]使得li~ri的区间和为质数,-1e7<=xi<=1e7。
思路反思:这道题可以说是这场打的最差的一题了,一开始的时候思路并不是我想的,所以当队友陷入代码冗余,debug困难的时候我就接手了重构代码的任务。队友认为区间和<=2logn时,是可以找到一个合法区间的。所以对于普通的xi,我们考虑不包含xi的区间[l,r](l>xi),对于>0的xi,我们考虑枚举长度不超过2logn的区间。然后。。。。快乐的收获了一个TLE。但实际上在实现的过程中我们并没有具体的考虑这个2logn是否正确,并且由于我提出了评测机非常快,所以我们直接上的log^2n的枚举区间的做法,获得了TLE。这时候其实最应该做的就是重新审视题目并且得到一些这道题具有的特质。而且我们还认为1e7内的质数密度大概在logn区间内有一个,而实际上在赛后枚举取max后发现,两个质数的距离可以达到210,远高于预期。而这题的关键在于我们要查询的一个值是一个连续区间的和。这个性质非常的好。我们发现一个区间的和为中位数*区间长度。也就意味着当区间长度>=3时,区间和必然不可能是质数。所以题目就这么解决了,我们枚举210内的长度为2的区间,再找到后一个质数,两种方案取个min即可。
1004.Decomposition
题意:n个点的完全图,n为奇数,要找到k条路径,路径长度给定,这k条路径互不相交,并且每条路径不能经过重复点,保证k条路径的并是完全图本身,每条路径长度不超过n-3
思路反思:这题虽然队友看错题了。但是也是一个很有趣的做法。我们稍微改变一下题意,若k条路径是不能经过重复边。队友相处了一个有趣的构造。我们考虑枚举k=2,3,4,..... n/2作为间隔,然后将一堆环连成一个欧拉回路。那么当gcd(k,n)=1时,他会遍历所有的n个点并最终回到1,而当gcd(k,n)!=1时,诸如n=9,k=3则会产生 0 3 6 0;1 4 7 1;2 5 8 2;等的环,那么我们在%gcd意义下的vector插入每个环,最终将每个vector用邻边链接起来,就可以获得一个欧拉路径。但是这题是不允许这么做的。
然后回到这道题。这题原题我原原本本的做过,当时的我还是能够很好的思考出这种题的,只能说经过一个寒假之后我再也没有这么好的状态了,只能慢慢恢复吧。
显然我们希望构造出一种比较方便旋转or对称的路径,使得这条路径的长度大概在n的级别。首先应该想到的就是折线。诸如:
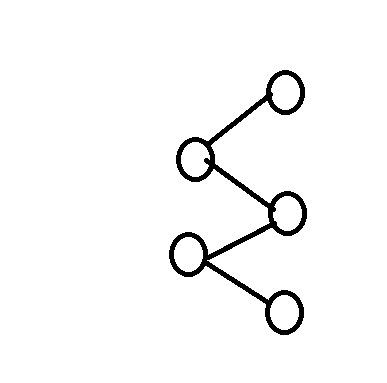
但是我们发现如若是奇数个点构成的折线,我们很难做旋转or对称,因为多了一个点之后会很容易搞出重边和缺边。我们考虑将多的这一个点放到合适的地方。放在外侧显然不可取,我们考虑放在中间。
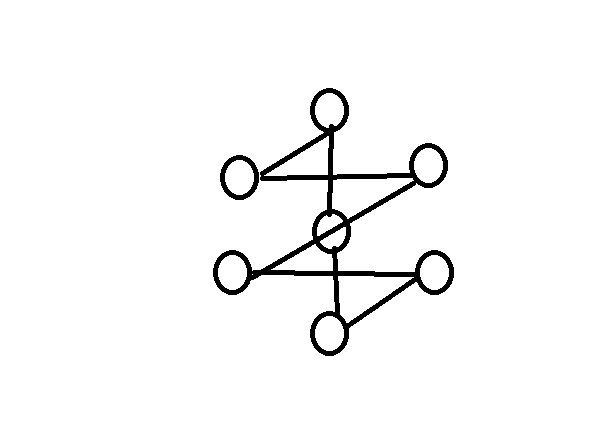 此时我们惊奇的发现这是一个非常适合旋转的结构!实际上只要旋转n/2次就可以得到一个完全图!这样我们只需要简单的构造+输出方案即可。
此时我们惊奇的发现这是一个非常适合旋转的结构!实际上只要旋转n/2次就可以得到一个完全图!这样我们只需要简单的构造+输出方案即可。
1005.Median
题意:给定1~n的n个数,其中有m个数被选中,你需要将1~n分配到m个集合使得这m个集合的中位数为给定的ai。其中中位数定义为c[(i+1)/2](i为集合长度),问是否存在方案。
思路反思:这题是我开出来的,题目翻译出来就是第i个集合里比ai小的数=比ai大的数或者右边比左边大1。
首先有一个很显然的策略,就是按照权值对ai排序之后,对于ai左侧的数,显然塞到ai这个集合里比较优,因为如果塞到后续集合里只会变得更劣。因为塞到后续集合只会使得r的选取区间变得更小,显然不会更优。
我一开场的思路是考虑最后一个集合后面的数,假设有r个,那么a[m]<r时必然无解。然后我们考虑将a[m]左边的数尽量的消耗,如果消耗到最多时,l(左边剩余的空隙)仍然>r则无解,其余情况都必定有解。这个想法本身是没有问题的。问题在于我考虑如何消耗的最多的时候陷入了困境,当对第i个集合考虑的时候,左端点肯定选一个比ai小的,但是右端点的选取方法没有特别的贪心,选最靠左的和最靠右的都不是最合理的策略。我也考虑能不能通过改变一个点的所属权来反悔操作或者调整方案,但是没什么思路。
实际上我考场时的第一感觉是没错的。这题既然回答YES/NO,那么构造方案本身就是困难的。特化问题只会让题目更复杂,即考虑最后一个集合,因为考虑之后问题并没有得到完全的简化,仍然是一个复杂的配对问题。正确的思路应该是考虑区间的某些性质,单纯对一些充要条件进行check。当思考到这一点的时候我就需要果断放弃构造序列本身了,这才是及时止损的关键所在。
这题的解法是十分有趣的。我们先考虑一个比较直观的方法。对于第一个集合,如果左侧的空隙个数为x个,那么右侧需要至少有x,至多有x+1个位置与x匹配。当枚举到第i个集合时,我们考虑右侧的集合的空隙的位置个数应该满足什么条件。假设第i-1个集合需要至少a个位置,至多b个位置,我们可以至多供出c个空隙,首先我们必须保证a<=c<=b,否则无解,那么我们考虑两个极端:c尽量满足i-1前的集合,c全部给第i个集合,可以发现第i个集合右侧至少要c-a个位置,至多需要b+c+1个位置。这个解法就跟我们特化后的问题本质上是一样的,我们期望找到内耗最多(右侧至少x个位置)的一个条件,内耗最少(至多y个位置)的一个条件,若cntr满足这两个条件则为YES。所以其实如果我们将最后一个判定推广,则我们就能想出这个做法了。
第二个解法就是题解的写法。在我贪心匹配的时候我就发现,最终无法匹配的一定是一个夹在两个中位数之间的一段区间,那么这段区间什么时候可以被调整,什么时候无解呢?我们发现一个事情,就是考虑暴力填满这个区间,即长度len-前面的中位数个数(使用右侧+1的权利)仍然大于剩余的数的个数:n-m-len,那么必然是无解的。如若细心证明即可发现反之一定有解。这个证明较为复杂,之后会补上的。