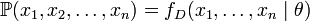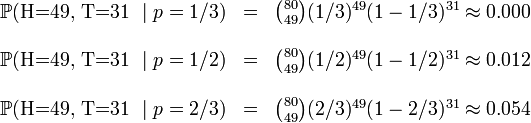维基百科,自由的百科全书
最大似然估计是一种统计方法,它用来求一个样本集的相关概率密度函数的参数。这个方法最早是遗传学家以及统计学家罗纳德·费雪爵士在1912年至1922年间开始使用的。
预备知识
下边的讨论要求读者熟悉概率论中的基本定义,如概率分布、概率密度函数、随机变量、数学期望等。同时,还要求读者熟悉连续实函数的基本技巧,比如使用微分来求一个函数的极值(即极大值或极小值)。
最大似然估计的原理
给定一个概率分布 ,假定其概率密度函数(连续分布)或概率聚集函数(离散分布)为
,假定其概率密度函数(连续分布)或概率聚集函数(离散分布)为 ,以及一个分布参数
,以及一个分布参数 ,我们可以从这个分布中抽出一个具有
,我们可以从这个分布中抽出一个具有 个值的采样
个值的采样 ,通过利用
,通过利用 ,我们就能计算出其概率:
,我们就能计算出其概率:
但是,我们可能不知道 的值,尽管我们知道这些采样数据来自于分布
的值,尽管我们知道这些采样数据来自于分布 。那么我们如何才能估计出
。那么我们如何才能估计出 呢?一个自然的想法是从这个分布中抽出一个具有
呢?一个自然的想法是从这个分布中抽出一个具有 个值的采样
个值的采样 ,然后用这些采样数据来估计
,然后用这些采样数据来估计 .
.
一旦我们获得 ,我们就能从中找到一个关于
,我们就能从中找到一个关于 的估计。最大似然估计会寻找关于
的估计。最大似然估计会寻找关于 的最可能的值(即,在所有可能的
的最可能的值(即,在所有可能的 取值中,寻找一个值使这个采样的“可能性”最大化)。这种方法正好同一些其他的估计方法不同,如
取值中,寻找一个值使这个采样的“可能性”最大化)。这种方法正好同一些其他的估计方法不同,如 的非偏估计,非偏估计未必会输出一个最可能的值,而是会输出一个既不高估也不低估的
的非偏估计,非偏估计未必会输出一个最可能的值,而是会输出一个既不高估也不低估的 值。
值。
要在数学上实现最大似然估计法,我们首先要定义似然函数:
并且在 的所有取值上,使这个函数最大化。这个使可能性最大的
的所有取值上,使这个函数最大化。这个使可能性最大的 值即被称为
值即被称为 的最大似然估计。
的最大似然估计。
注意
- 这里的似然函数是指
 不变时,关于
不变时,关于 的一个函数。
的一个函数。 - 最大似然估计函数不一定是惟一的,甚至不一定存在。
例子
离散分布,离散有限参数空间
考虑一个抛硬币的例子。假设这个硬币正面跟反面轻重不同。我们把这个硬币抛80次(即,我们获取一个采样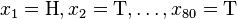 并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为
并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为 ,抛出一个反面的概率记为
,抛出一个反面的概率记为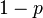 (因此,这里的
(因此,这里的 即相当于上边的
即相当于上边的 )。假设我们抛出了49个正面,31个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为
)。假设我们抛出了49个正面,31个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为 ,
,  ,
,  .这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个:
.这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个:
我们可以看到当 时,似然函数取得最大值。这就是
时,似然函数取得最大值。这就是 的最大似然估计。
的最大似然估计。
由上可知最大似然估计的一般求解过程:
- 写出似然函数;
- 对似然函数取对数,并整理;
- 求导数;
- 解似然方程。
注意:最大似然估计只考虑某个模型能产生某个给定观察序列的概率。而未考虑该模型本身的概率。这点与最大后验概率估计不同。