0.PTA总分

1.本周学习总结
1.1 总结图内容
图存储结构
- 邻接矩阵
简单来讲使用二维数组进行存储,设位edge[M][N]。其中,M,N代表两个顶点,edge[M][N]可代表是否连通或者权值。
邻接矩阵的特点:
- 若图为无向图,则矩阵是沿对角线是对称的。
- 可以直接访问顶点M,N间边的关系以及权值。
缺点:
- 存储的图为稀疏图时,浪费的空间较多,n个顶点所需空间至少为n^2。
结构体定义
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,边数
} MGraph;
- 邻接表
采用结构体数组跟链表结合,存储每个顶点的临边
特点:
- 存储的图为无向图时,遍历顶点数组每个临边即可遍历整张图
- 相比于邻接矩阵更节省空间
缺点
- 无法直接知道任一两个顶点之间的关系。
- 存储的图为有向图时,同一条边会生成两条链。
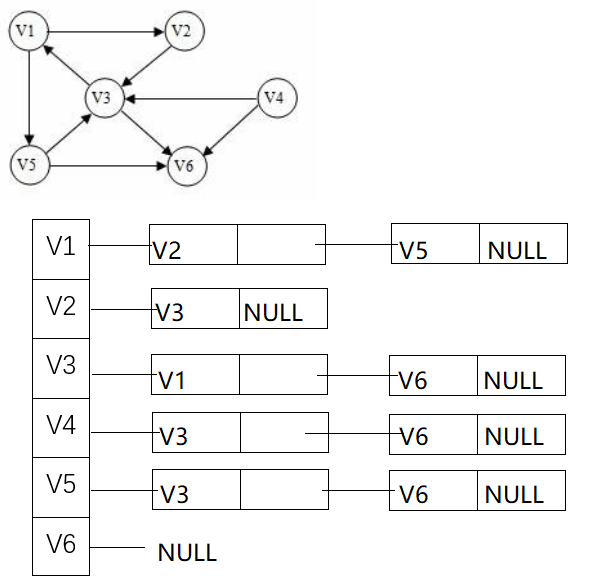
结构体定义
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV]; //头结点数组
typedef struct
{
AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
图遍历及应用
- 遍历
图的遍历总的分为两种:
1.深度优先搜索(Depth-First-Search)简称为DFS。
可对比于二叉树的先序遍历。只要当前节点仍有未访问的邻接点,就继续访问,直到尽头。
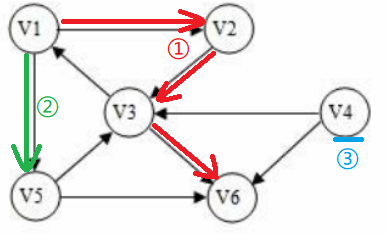
邻接矩阵DFS代码
void DFS(MGraph g, int v)
{
int i, j;
visited[v] = 1; //v元素已被访问
if (flag == 0)
{
flag = 1;
cout << v;
}
else
{
cout <<" "<< v;
}
for (j = 1; j <= g.n; j++)
{
if (g.edges[v][j] ==1 && visited[j] != 1) //寻找未被访问的邻接点
{
DFS(g, j);
}
}
}
邻接表DFS代码
void DFS(AdjGraph* G, int v)
{
ArcNode* p;
int a;
p = G->adjlist[v].firstarc; //v顶点指向的第一条边
visited[v] = 1; //v节点已被访问
if (flag == 0)
{
flag = 1;
cout << v;
}
else
{
cout << " " << v;
}
while(p!=NULL) //遍历v节点邻边,寻找未访问的节点
{
a = p->adjvex;
if (visited[a] != 1)
{
DFS(G, a);
}
p = p->nextarc;
}
}
- 广度优先搜索(Breadth-First-Search)简称为BFS。
可对比于二叉树的层次遍历。根节点入队,每次出队一个元素,将其所有邻边入队,直到队空。
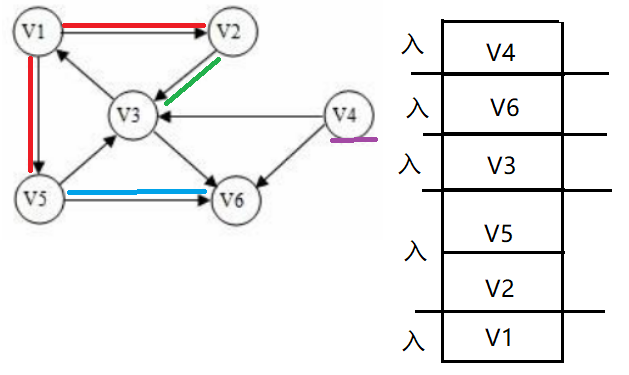
邻接矩阵BFS代码
void BFS(MGraph g, int v)
{
queue<int>q;
int top;
int j;
visited[v] = 1; //v元素被访问
cout << v;
q.push(v); //入队根节点
while (!q.empty())
{
top = q.front(); //取队头元素,并出队
q.pop();
for (j = 1; j <= g.n; j++)
{
if (g.edges[top][j] == 1 && visited[j] != 1)
{
cout << " " << j;
visited[j] = 1; //入队所有未被访问的邻接点
q.push(j);
}
}
}
}
邻接表BFS代码
void BFS(AdjGraph* G, int v)
{
queue<int>q;
ArcNode* p;
int top;
int a;
visited[v] = 1; //v元素被访问
q.push(v); //入队根节点
cout << v;
while (!q.empty())
{
top = q.front();
p = G->adjlist[top].firstarc; //取队头元素指向的第一条边
q.pop();
while (p)
{
a = p->adjvex;
if (visited[a] != 1)
{
q.push(a); //遍历其所有邻接点,入队未访问节点
visited[a] = 1;
cout << " " << a;
}
p = p->nextarc;
}
}
}
- 判断图是否连通
连通图:如果图中任意两点都有路径相连通,那么图被称作连通图。如果图是有向图,则称为强连通图。
根据定义,我们就可以很好的解决如何判断图是否连通了。我们只需对图任一一个顶点进行一次DFS或BFS即可,最终只需判断已访问的顶点数跟总顶点数是否一致。
bool JudgeG(MGraph g, int v)
{
int count;
count = BFS(g,v);//对v顶点经行一次BFS
if count!=g.n //遍历的顶点数不等于总顶点数时
return false;
return true;
}
- 最短路径
- Dijkstra算法
算法讲顶点分为两部分S(入选顶点)T(未入选顶点),并采用了dist[]与path[]数组
for i=0 to n
{
if v跟i间有边
path[i]=v;
dist[i]=edge[v][i];
else
path[i]=-1;
dist[i]=inf;
}//初始化dist数组,path数组
遍历图中所有节点
{
for(i=0;i<g.n;i++) //找最短dist
{
若s[i]!=0,则dist数组找最短路径,顶点为u
}
s[u]=1 //加入选中数组S,说明顶点已选
for(i=0;i<g.n;i++) //修正dist
{
if i未选 && dist[i]>dist[u]+u到i的距离
则 dist[i]= dist[i]>dist[u]+g.edges[u][i]
path[i]=u;
}
}
Dijkstra算法的缺点:
- 所求最短路径图不能带负权值。
- 不能够用于求最长路径。
- Floyd算法
采用矩阵来进行操作,A[],path[][]
其每次取一个顶点 k 为中间衔接点,若 i 到 j 的距离大于 i 到 k 的距离加上 k 到 j 的距离,则修正A[i][j]=A[i][k]+A[k][j],path[i][j]=k。直到顶点遍历完成
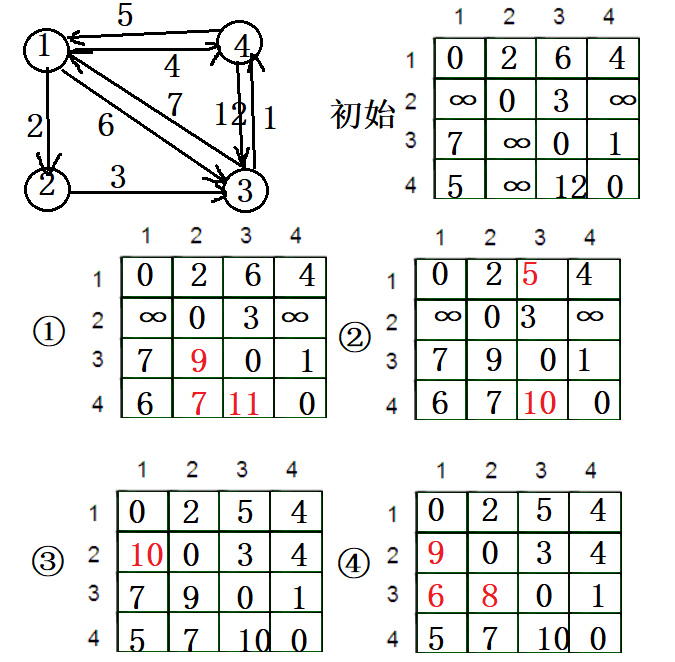
for (k=0;k<g.n;k++) //求A与path
{
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
if (A[i][j]>A[i][k]+A[k][j]) //找到更短路径
{
A[i][j]=A[i][k]+A[k][j]; //修改路径长度
path[i][j]=k; //修改经过顶点k
}
}
- 最小生成树
- prim算法
采用两个辅助数组closest[]存未入选顶点距离最近的已选顶点,lowcost[]存closest[k]到k之间的距离。
每次从lowcost数组中挑选最短边节点k输出(将lowcost[k]=0,表示已选),若新加入的顶点使得未加入顶点最短边有变化则修正closest跟lowcost数组。循环直到所有节点入选。
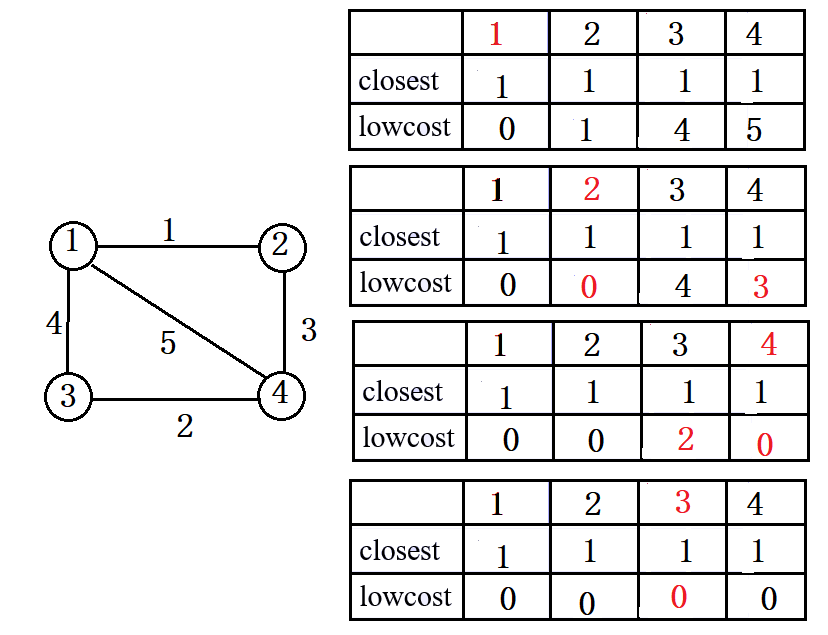
- prim算法
for (i=1;i<g.n;i++) //找出n-1个顶点,初始顶点默认已选
{
min=INF;
for (j=0;j<g.n;j++) // 找未选顶点到已选顶点最小值
if (lowcost[j]!=0 && lowcost[j]<min) //j未选并且边最小
{
min=lowcost[j]; k=j; /k记录最近顶点的编号
}
cout>>k;
lowcost[k]=0; //k已选
for (j=0;j<g.n;j++) //修正数组lowcost和closest
if (lowcost[j]!=0 && g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k;
}
}
2. Kruskal算法
对我而言,该算法比prim算法易于理解,但代码量较多与prim算法。
算法将所有边权值进行排序。依次从小选取边,若选取的边没有使图形成环路,则入选该边,直到选满n-1一条边为止。
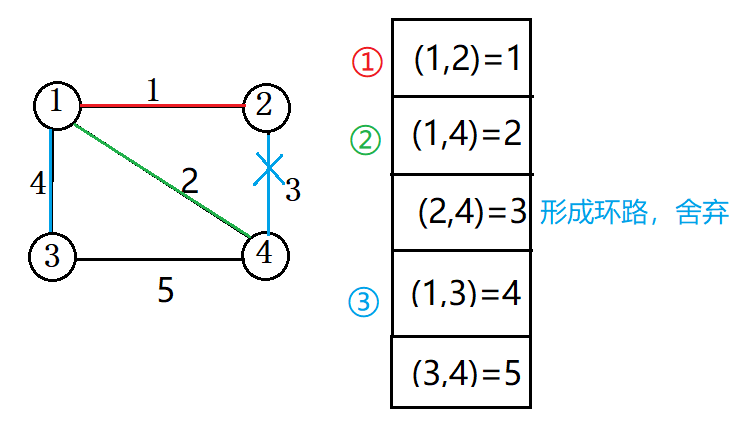
是否构成环路问题可用并查集知识点来解决
//边结构体
typedef struct
{ int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
} Edge;
void Kruskal(AdjGraph *g)
{
初始化边数组Edge E[MAX];
将E数组对边的权值进行排序;
初始化并查集树t;
j=1; //E中边的下标,初值为1
while 生成的边数小于n-1
{
取sn1跟sn2为E[j].u跟E[j].v的集合;
if sn1!=sn2
输出该边,并合并两顶点所在集合;
}
-
应用:公路村村通
本题我采用了vector数组以及排序函数sort,这可能会使得编写起来较为容易


-
拓扑排序
拓扑排序的对象只能是有向无环图
因此拓扑排序可用于判断图是否有环。
每次取入度为0的节点,并将其邻接点入度-1,做类似删除操作,但实际并没有。循环直至入选所有节点
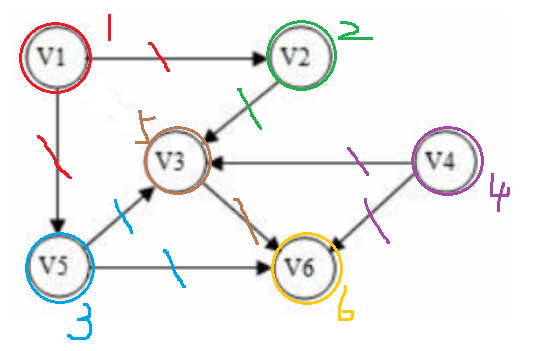
遍历图,将每个顶点的入度存入count[]数组;
遍历顶点
入栈入度为0的顶点
while 栈不空
{
出栈节点V;
遍历V的所有邻接点
{
入度-1;
若入度为0,入栈
}
}
求所有顶点的入度(邻接表)
for (i=0;i<G->n;i++)
{
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
G->adjlist[p->adjvex].count++;
p=p->nextarc;
}
}
for (i=0;i<G->n;i++) //将入度为0的顶点进栈
if (G->adjlist[i].count==0)
{
top++;
St[top]=i;
}
栈内循环
while (top>-1) //栈不空循环
{
i=St[top];top--; //出栈顶点i
p=G->adjlist[i].firstarc;
while (p!=NULL) //遍历顶点i所有邻接点
{
j=p->adjvex;
G->adjlist[j].count--; //入度-1
if (G->adjlist[j].count==0) //入度为0进栈
{
top++;
St[top]=j;
}
p=p->nextarc;
}
}
- 关键路径
求关键路径有两个重要概念:时间V的最早开始时间ve以及最迟开始时间vl。
其中vl要在ve的基础上才能求得
关键活动则要通过ve,vl求得:引入e,l,其中e=ve而l=vl-dut(顶点间权值)。当e==l时该活动称为关键活动,将所有关键活动连起来,则是关键路径。
需要注意的是:关键路径要在拓扑排序的基础上进行
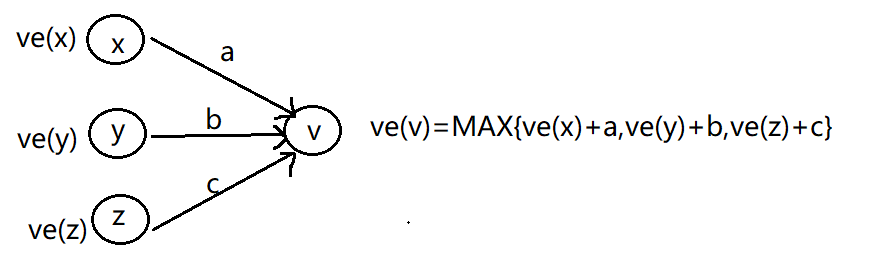
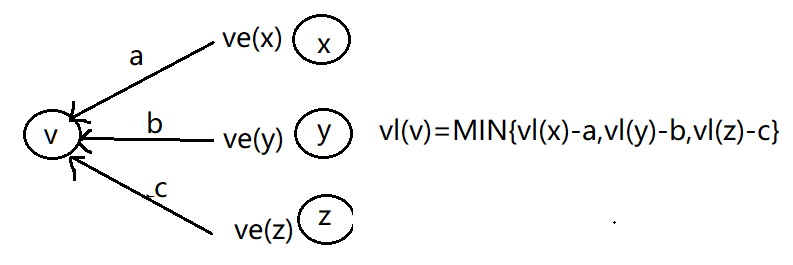
以测试题为例
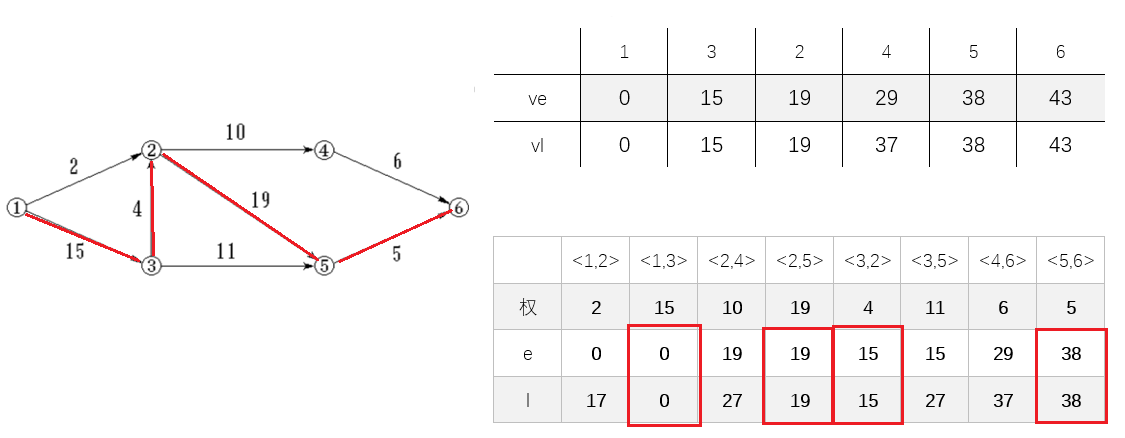
1.2.图的认识及学习体会。
根据之前的内容,相当于是循循渐进的过程,从 一对一 到 一对多 到图的 多对多 ,一个逐步认知的过程。当我个人觉得图这章内容更易于树,本章相对于树没有太多链与链之间的关系,可能操作起来会比较的简单。但是由于图的关系更深入,部分知识点理解起来也会比较的困难。尤其是感觉最近课程比较赶,可能还需要一些时间更好的消化。
2.阅读代码
2.1 84. 柱状图中最大的矩形
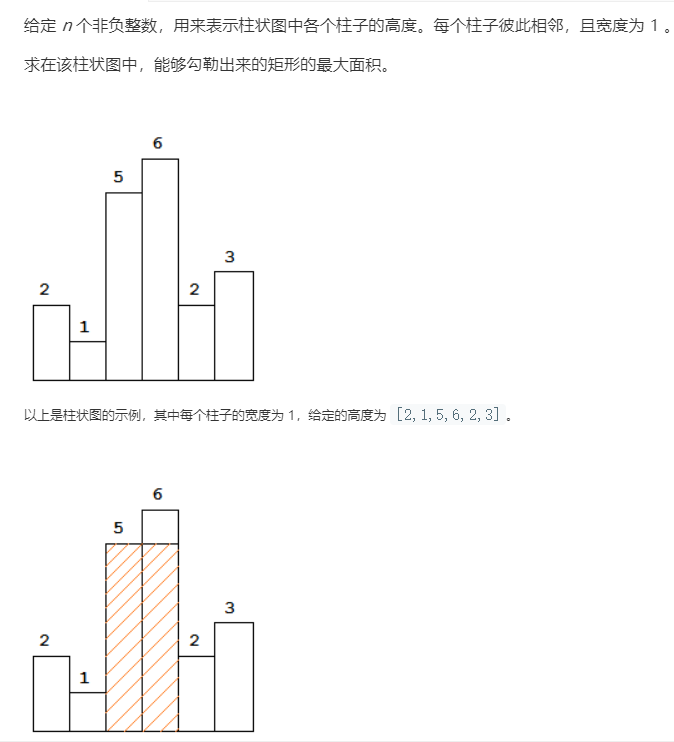

代码
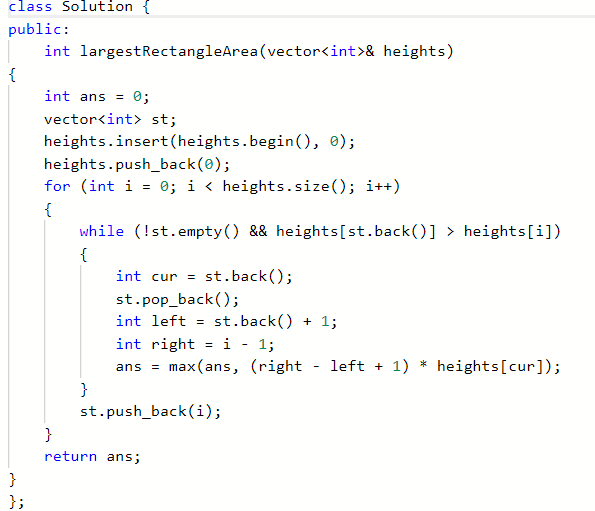
2.1.1 该题的设计思路
使用单向栈,单向栈即栈内元素保持单调递增或递减。
思路:对每个高度求其宽度,就能得到每个高度下的面积,取最大值即可。
应用到单向栈,使得栈中从小到大排列,所以栈中后面元素高度一定大于前面元素,相当于宽度可以一直延伸,直到进栈元素低于栈顶时出栈并开始计算面积,出栈直到栈顶高度小于进栈元素。
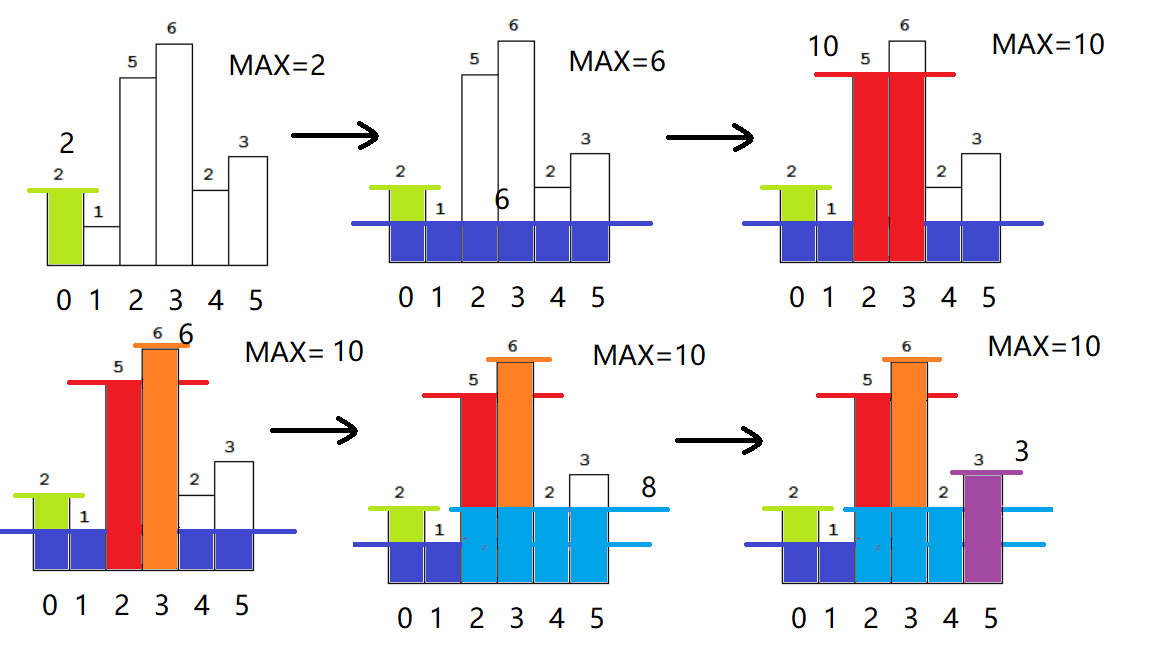
由于每个元素都将出入栈一次时间复杂度:O(n)
栈中存储元素n个空间复杂度:O(n)
2.1.2 该题的伪代码
先将0进栈,保证初始栈顶有元素;
while (遍历所有高度hights[i])
{
while (栈非空&& 进栈元素小于栈顶时)
{
取栈顶元素top;
求矩形宽度w;
面积S = top * w;
最大面积MaxS = max(MaxS, S);
}
入栈hight[i];
}
2.1.3 运行结果
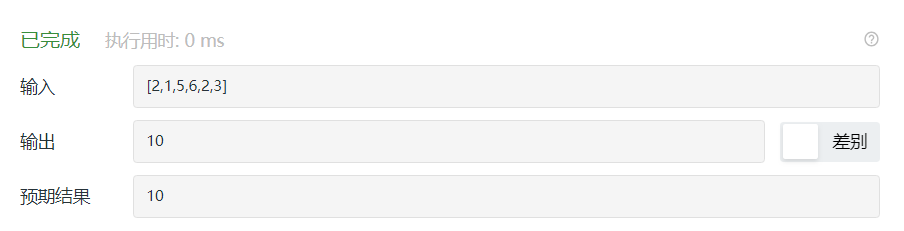
2.1.4分析该题目解题优势及难点
1.难点:单向栈概念的引入,刚开始时我疑惑了一会才知道这个栈怎么实现的程序。通过栈内数据来模拟成一个高度的最大宽度,从而实现算法。
2.优势:看到题目时我最先想到的是通过计算所有柱之间最小高度再乘以宽度得出面积,再统计最大面积,相当于暴力算法。显然是不如采用栈所得的效率。
2.2 785. 判断二分图

代码

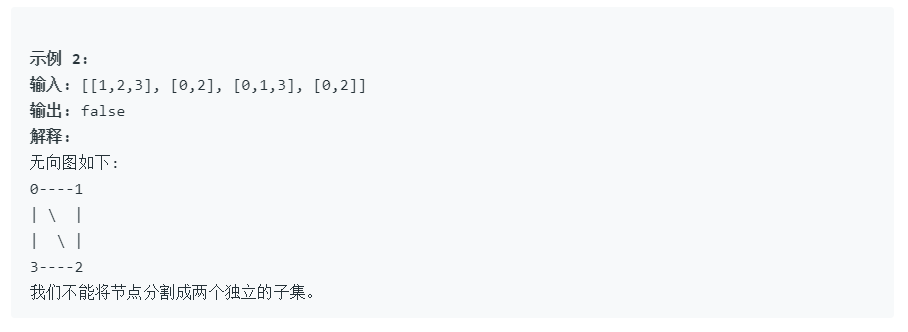
2.2.1 该题的设计思路
将二分图问题转化为着色问题,分为2种颜色。通过DFS进行着色,若在DFS过程中发现邻接点已经着色且颜色相同,说明不构成二分图。
时间复杂度O(n+e)n为顶点数e为边数;
空间复杂度O(n)color数组存顶点颜色。
2.2.2 该题的伪代码
for 遍历顶点
{
if 顶点v未被着色
{
将v着色成color
for 遍历v的邻接点
{
if 邻接点color与v的相同 return false;
else if 邻接点未着色
递归将邻接点着色成-color
}
}
}
return true;
2.2.3 运行结果

2.2.4分析该题目解题优势及难点
1.难点就在于能不能将二分图的判别方法转化为图的着色问题。
2.优势在于题解是在DFS过程中同时着色跟判断,这会提升不少效率。
2.3 802. 找到最终的安全状态
代码

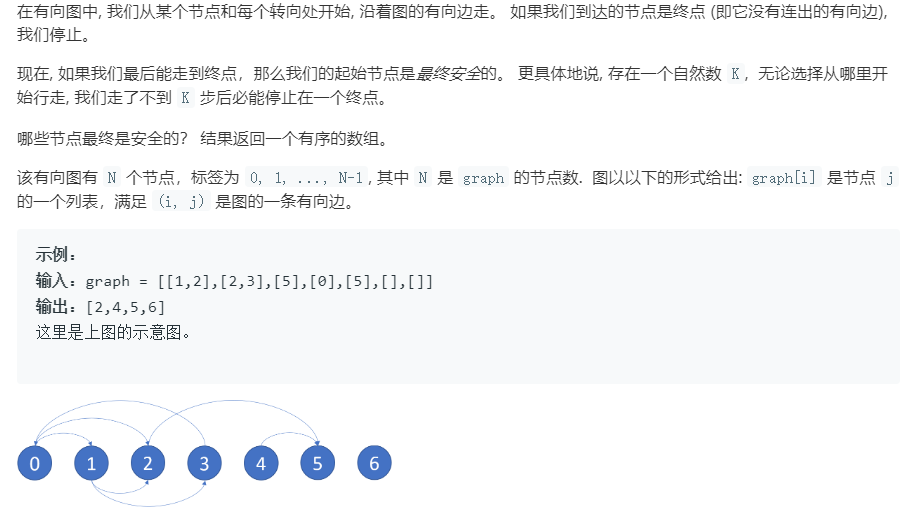
2.3.1 该题的设计思路
采用拓扑排序的思想。图中没有出边的顶点一定是安全的,将此顶点删除,剩下顶点中没有出边顶点也是安全的,以此类推,找到所有安全节点。
将top排序中对入度操作改为对出度的操作即可。
2.2.2 该题的伪代码
for 遍历顶点
{
if 顶点v出度度为0
v入队列
}
while 队列非空
{
出队top
for 将top所有邻接点出度度减一
{
if (邻接点出度度为0)
邻接点入队
}
}
2.2.3 运行结果
2.2.4分析该题目解题优势及难点
1.优势:由于图是用vector数组存储,只需通过graph[i].size()即可知道顶点i的出度。
2.难点:能否看出安全状态与top排序之间的关系。