红黑树
定义:
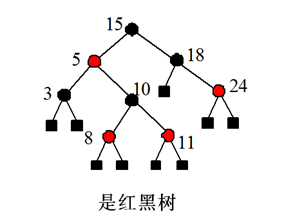
带有外部结点,且满足下列条件的二叉树:
1)每个结点都有标为红色,或黑色
2)根结点为红色
3)外结点为黑色
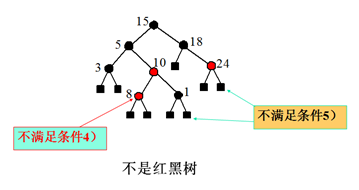
4)[红不相邻]每个红结点的儿子必为黑结点
5)根(包括子树的根)到外结点的每条路径上,标记为黑色的结点数相同
结点数与高度之间的关系:
定理:
1.具有n个内结点的红黑树,高度h≤2log(n+1)。
2.结点x的黑高bh(x)等于x到达其子孙叶子的任意路径上遇到的黑色结点的数目(不包括x本身)。
3.结点x的非空子孙数≥2bh(x)-1 。
旋转方法:
红黑树属于二叉平衡检索树
对红黑树插入删除时,若破坏了黑平衡
则要对其进行调整(通过旋转)
旋转方法——左旋、右旋,二者对称
要求:保中序、保黑平衡
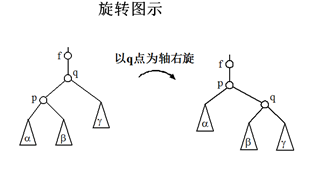
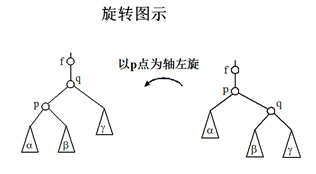
红黑树插入算法
void rb_insert(elem_type x)
{ //插入阶段
1. 按一般检索树的插入方法插入x,用新结点x代替某个外结点
2. 将x标记为红色//为保黑平衡,新结点总是先标为红色
//回溯阶段
3. 设p是指向新结点x的指针
4. while(1)
5. { if(p是根) {将结点p标成黑色; return;}
6. if(p之父是黑色) return;
//至此,p不是根,并且p之父为红色,而且p之父也不是根
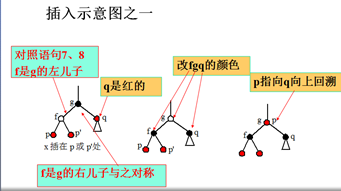
7. 用f指向p之父,g指向f之父;
8. if(f是g的左儿子) //f是g的右儿子处理步骤与之对称
9. { 用q指向g的右儿子; //即q是p的“叔叔”
10. if(q为红色)
11. {将f和q改为黑色,将g改为红色; //g原为黑色
12. 令p指向g;
13. coninue;
} //因g改为红色后,会造成“红相邻”,要向上层回溯
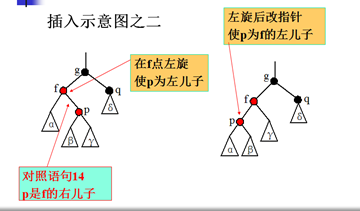
14. if(p是f的右儿子)在f点左旋,并调整指针;
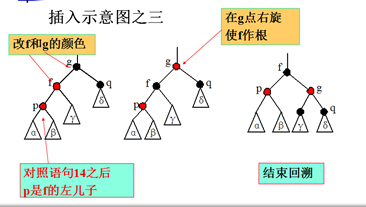
15. 将p的父亲f改为黑色,将f的父亲g改为红色;
16. 在g点右旋;
17. return;
}
else {与语句9~17对称,处理f是g的右儿子的情况}
} //与语句5的左括号对应
} //与最外层左括号对应
图示
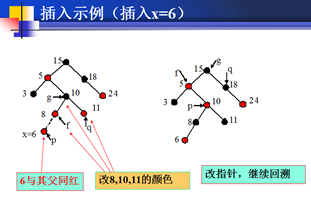
插入示例图
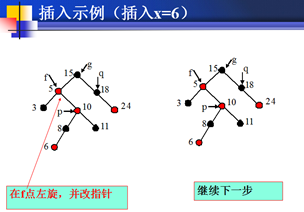
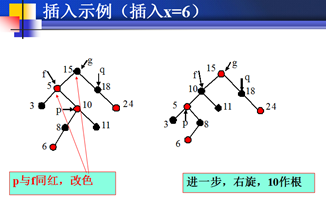
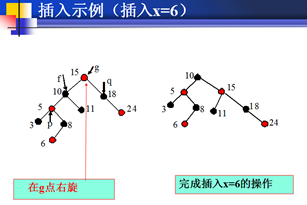
删除操作的基本原理
像一般检索树那样,找到要删除的结点x,若x有两个儿子,真删除的是x的中序前驱
于是,被删除结点或是叶,或只有一个儿子,删除后,要接好断枝。
如果被删除结点f是红的,不要回溯,算法终止。
如果被删除结点f是黑的,破坏了红黑树条件
分下列3种情况,分别进行处理:
1)f是根结点,而且代替f的红儿子p作新根(破坏了条件2),只要将新根p改为黑的就行了。
2)f的儿子p是红的,而f的父亲g也是红色的,用p代替f作g的儿子时,发生红冲突,破坏了条件4,只要将p改为黑的就行了。
3)f的儿子p是黑的,用p代替f,将导致p所在的那条路径上黑色结点减少,破坏了条件5,要考虑如何恢复黑平衡。
当删除黑色结点f,让其黑儿子p代替它时,给p“附加”一个虚拟黑色,使p成为既有原来的颜色,又有虚拟黑色的一个“双色结点”,使树仍然保持黑平衡(假想的)。
注意:
“双色结点”只是一个虚拟概念(帮助理解回溯过程中的黑平衡)。随着向上层回溯过程,原双色结点消失(保留原色),上层某个结点变成双色结点(双色上移)
双色结点上移过程,可能出现三种情况:
1)如果p是“红-黑”的,即p本来是红的。这种情况下,只要将p改为黑色,恢复其单色性,回溯终止
2)如果p指向根结点,在这种情况下,这个附加的黑色自动消失了,回溯终止
3)其他情况,则需要适当地旋转和改色
红黑树删除算法
void rb_delete(elem_type x)
1. { 在树中找到要删除的结点x,并用f指向x;
2. if(x有两个儿子) //被删除的将是x的中序前驱y
3. {找x的中序前驱y; 用y结点值代替x结点值;并用f指向y;}
//至此,f指向被删除结点,且f至多只有一个儿子
4. if(f的左儿子不空) p指向f的左儿子;
5. else p指向f的右儿子; //p有可能指向外结点
6. if(f是根){使p作根,并将p标为黑色; return;} //算法终止
7. else 让p代替f作为其父g的儿子; //删除了f
8. if(f是红的) return; //算法终止
9. if(f是黑的,而p是红的){ 将p标为黑色; return;}//算法终止
//至此,f和p都是黑的
10. while(p不是根,且p是黑的)
{
11. if(p是左儿子)//是右儿子的情况与之对称
12. { 用q指向p的兄弟;
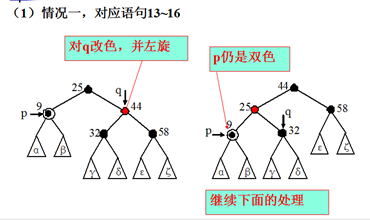
13. if(q是红的) //情况一
14. { 将q改为黑色, 将p之父改为红色;
15. 在p之父处左旋;
16. 将q重新指向p的新右兄弟;
}
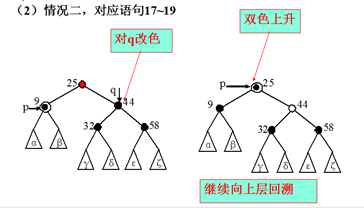
17. if(q的左右儿子都是黑的) //情况二,双色结点上升
18. { 将q改为红的;将p指向其父;
19. cotinue; //进入下一轮循环
}
else//与语句17的if配对,q的左右儿子不全是黑的
{
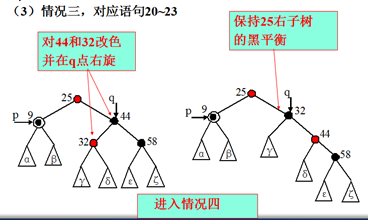
20. if(q的右儿子是黑的,而左儿子是红的) //情况三
21. { 将q的左儿子改黑, 将q改红;
22. 在q点右旋;
23. 将q重新指向p的新右兄弟;
} //至此q的右儿子是红的
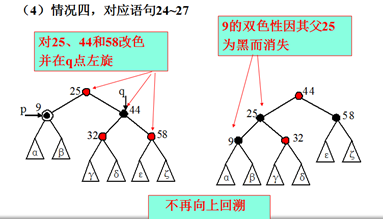
24. 将p之父的颜色赋给q;//情况四
25. 将p之父改为黑色, 将q的右儿子改黑;
26. 在p之父点处作左旋;
27. p指向根; //转到语句10,使循环终止,再转到语句29处
}
}
28. else {与语句12~27对称,处理p是f右儿子的情况}
}
29. 将p改为黑色;return;
}
图示