一个多元函数的梯度方向是该函数值增大最陡的方向。对于一元函数而言,梯度方向是沿着曲线切线的,然后取切线向上增长的方向为梯度方向。对于二元或多元函数而言,梯度向量为函数F对每个变量的导数,该向量的方向就是梯度的方向。
上图为一元二次函数的曲线图,可以看出:在最低点的左边部分,每一点的梯度方向值都是负值,因为每一点的斜率都是小于0的,所以当变量沿着梯度的方向递进,函数值越来越大,从上图可以很明显看出;同理右边,每一点的梯度方向都是大于0的,所以沿着梯度方向,函数值也是越来越大。所以,函数的梯度方向总是函数值越来越大的方向。因此,我们要想求最小值,就应该沿着梯度的反方向进行,这正是梯度下降法的原理。
梯度下降法(梯度上升法应该也适用)迭代结束的条件,常用的有两种:
一、定义一个合理的阈值,当两次迭代之间的差值小于该阈值时,迭代结束。
二、设置一个大概的迭代步数,比如1000或500,梯度下降法最终的迭代肯定会收敛,只要达到相应迭代次数,多了也没关系。因为迭代次数多了后,在
到达极值点时,函数对变量的导数已近乎为0,即使过了极值点,导数就变为正数了,之前的导数为负数。这个时候,变量x的值减去步长与导数的乘
积反倒变小了。所以即使步数多了,结果也基本上就在极值点处左右徘徊,几乎等于极值点,因此没有问题。
为什么梯度是下降最快的方向呢?
其实下降最快的方向在数学上被称为梯度方向而已,所以并不是什么梯度下降最快,而是最快的方向就被定义为梯度。那么什么方向下降最快呢,所谓下降最快其实就是这一点的斜率最大的方向。

上图Duf(x,y)表示的是曲面上任意方向的变化速率,即该点对应的斜率,因为曲面上过某点的切线有无数条,曲线上是只有一条。
根据上述解释我们举例函数z=x+y,依据上面推到则A=(1,1),I=(cosθ,sinθ),θ是任意变化速率方向与X轴的夹角,如下图所示:

所以当向量I转到与A平行的时候,方向导数最大,因为这个时候I跟A的夹角为0,斜率就等于|A|=√(12+12)=√2 ,此时I与X轴与y轴的夹角都为45°,因为A的方向是(1,1),所以这个时候sinθ和cosθ都是1/√2,然后fx(x,y)sinθ+fy(x,y)cosθ=√2 。
从几何图示上来解释,其实我们求的这个斜率就是针对x,y的变化,所引起的z轴数值的变化速率,当x,y从点(0,0)沿着梯度方向(1,1)变化的时候,z值由0变成了2,如下图所示:
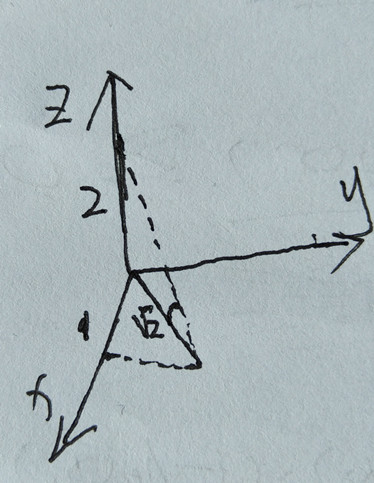
而x和y共同走的是下面的√2,所以斜率为2/√2=√2。同理如果梯度是(1,2),则梯度方向的斜率为√5,几何意义参考上图。
参考:https://mp.weixin.qq.com/s?__biz=MzI4MDYzNzg4Mw==&mid=2247483704&idx=1&sn=8f0c6e33ef84c26823e562be16bce684&chksm=ebb439ecdcc3b0fa4e9571deb33ccea62e42034c88db4e190633588307dce4a1e0c91ed2635c&scene=21#wechat_redirect
