一切从逻辑回归开始

JSong @2016.06.13

本系列文章不适合入门，是作者综合各方资源和个人理解而得. 另外最好有数学基础, 因为数学人一言不合就会上公式.

简单模型的魅力在于它能从各个角度去欣赏. 逻辑回归是最简单的二分类模型之一，实际应用中二分类最常见，如判定是否是垃圾邮件，是否是人脸，是否值得借贷等, 而概率模型对于这类问题有得天独厚的优势. 本文将从各个角度来理解逻辑回归，并指出它是一个概率模型、对数线性模型、交叉熵模型.

我们先从线性回归谈起。 考察 m 个变量和 y 之间的线性关系：

[ysim x_1+x_2+cdots +x_m ]

根据要求我们需要找到 m+1 个回归系数 θ_i，使得

[min ||y-hat{y}||_{F},quad hat{y}=h_{ heta}(x)=sum_{i=0}^m heta_i x_i= heta^T x ]

其中 x_0=1.

1. 线性代数下的回归模型

如果每个变量都有 n 个样本，即 x_i ∈ R^n ，则上述问题等价于求解线性方程组：

[X heta =y, quad X=(x_0,x_1,ldots,x_m) ]

一般来讲，上述方程有唯一解(最小二乘法)：

[ heta=X^{+}y=(X^TX)^{-1}X^Ty ]

讲到这，车就可以开始上路了。

2. 二分类问题简介

分类模型比较常见，例如是否是垃圾邮件等等。而最简单的分类就是二分类，且多分类一定程度也可以转化成二分类问题。 给定一组有标签的训练数据

[(X,y)={(x^{i}in mathbb{R}^n, y^{i}in {0,1}): i=1,2,ldots,m} ]

在下图中我们随机给了一组散点图，红色代表y=1，蓝色代表y=0.

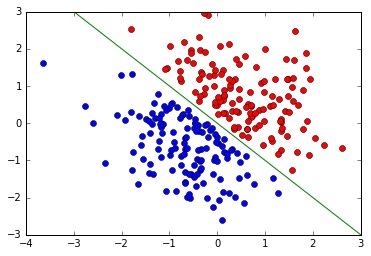
我们的目的就是找到一种模型将这两类样本点分开(当然实际应用中可能没有这么好的情况。 这里只是给一个Demo)。 最直接的想法就是找一个超平面

[ heta^T x=0 ]

使得红色点和蓝色点分别分布于超平面的两端. 此时对于任意一个样本点 x^{(i)}, 不失一般性

[ heta^T x^{(i)} ]

可以代表样本点到该超平面的距离。 因为红色样本点在超平面上方，即红点对应距离为正数，同理蓝点对应的距离为负数。 为避免区分红点或者蓝点，我们可以用

[(2y-1) heta^T x ]

来代替， 此时只要被正确分类， 该距离则为正数，否则为负数。 于是可得相应的损失函数为

[max(0,(2y-1) heta^T x) ]

综合一下可得最简单的线性分类模型为：

[arg_ heta min sum_{i=1}^{m} max(0,(2y_i-1) heta^T x^{(i)}) ]

这个损失函数有很多不好的地方，而且也不可导。接下来我们介绍更好的逻辑回归模型，其背后有很多的解释。

2.1 逻辑回归模型

令

[ heta^T x= heta_0 +sum_{i=1}^{m} heta_i x_i ]

且我们假定

[P(y=1|x; heta)=h_{ heta}(x)=g( heta^T x)=frac{1}{1+e^{- heta^T x}} ]

[P(y=0|x; heta)=1-h_{ heta}(x) ]

其中

[g(z)=frac{1}{1+e^{-z}} ]

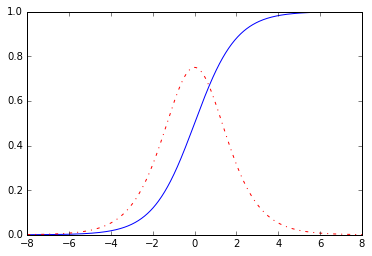
是 logistic 分布函数，它的图像和密度函数

[e^{-z}/(1+e^{-z})^2 ]

图像见下图. 原则上任何连续的分布函数都可以，其把实数映射到0到1之间. 至于为啥选择logistic函数, 我们之后再讨论.

这里我们采用极大似然估计. 由于y取值的特殊性, 上面的模型假设等价于

[P(y|x; heta)=(h_{ heta}(x))^y \,(1-h_{ heta}(x))^{1-y} ]

这样我们便有似然函数：

[l( heta)=log L( heta)=log prod_{i=1}^{m} p(y^{(i)}|x^{(i)}; heta) ]

[=sum_{i=1}^m [y^{(i)} log h_{ heta}(x^{(i)})+ (1-y^{(i)}) log (1-h_{ heta}(x^{(i)})] ]

于是得到逻辑回归模型为

[arg_{ heta} max l( heta) ]

2.2 几何意义（超平面分类）

重新考虑模型假设, 我们可以得到

[ heta^T x=log frac{p}{1-p}, quad p=P(y=1|x) ]

同样，逻辑回归模型也是用超平面来分类的. 且相应的极大似然估计可以写成

[min -l( heta)= sum_{i=1}^{m} log[(2y-1)(y-h_{ heta}(x))]=sum_{i=1}^{m} log (1+e^{(2y-1) heta^T x}) ]

也即相应的损失函数为

[log(1+exp((2y-1) heta^T x)) ]

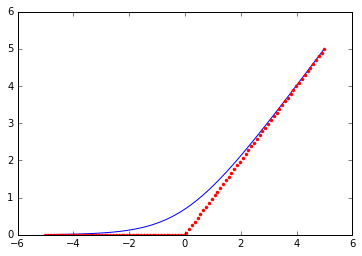
图像见下方. 由统计假设可知，给定一个样本点，如果它被正确分类，则

[(2y-1)(y-h_{ heta}(x)) ]

应该越小越好, 如y=1时,h_θ(x)越接近1越好. 相应的 (2y−1)θ^Tx 也是越小越好. 又根据第一节的讨论我们有, 当某样本点被正确分类时

[(2y-1) heta^T x= mbox{distance of sample point and hyperplane}\,\, heta^T x=0 ]

此处

[log(1+exp(x)) quad and quad max(0,x) ]

的作用类似，但连续性更好. 另外有些文章会写逻辑回归的损失函数为

[log(1+exp(-ycdot heta^T x)) ]

这是因为该损失函数中的 y 取值范围为-1和1.

2.3 线性代数意义

在上一节，我们给出了表达式

[ heta^T x=log frac{p}{1-p}, quad p=P(y=1|x) ]

可以看出它相当于把 y 映射到了[0,1]区间。而且 p/(1-p) 是事件发生与事件不发生的概率之比，称为事件的发生比 (the odds of experiencing an event), 简称为 odds 。

2.4 信息论解释(交叉熵模型)

令随机变量

[pin {y,1-y}, quad q in{hat{y},1-hat{y}} ]

其中 hat{y} 为模型拟合得到的y, 则它们之间的交叉熵 (cross entropy) 为

[H(p,q)= -sum_i p_i log q_i =-[ylog hat{y}+(1-y)log(1-hat{y})] ]

我们知道熵常用于度量一个随机变量所包含的信息量， 而交叉熵可以用来度量两个随机变量之间的相似性, 从上面式子可以看出逻辑回归的极大似然等价于最小化交叉熵.

事实上真正等价的是交叉熵与极大似然估计，有兴趣的同学可以自己证明。

2.5 神经网络模型

这个就不多说了，逻辑回归是一个最简单的神经网络模型

2.6 梯度下降法参数求解

按照极大似然的来求导：

[igtriangledown_{ heta} l( heta)=sum_{i=1}^{m} (y^{(i)}-h_{ heta}(x^{(i)}))x^{(i)}= X^T[Y-h_{ heta}(X)] ]

其中 x^{(i)} 在 X 中作为行向量存储. 于是可得参数 θ 的迭代式：

[ heta:= heta+alpha X^T[Y-h_{ heta}(X)] ]

其中 α 为步长, 另外因为是最大化 l(θ) ，所以是沿着梯度的正方向寻找。

1.7 python代码

import numpy as np
import matplotlib.pyplot as plt
import time
%pylab inline

# calculate the sigmoid function
def sigmoid(inX):
    return 1.0 / (1 + np.exp(-inX))



def trainLogRegres(train_x, train_y, opts):
    # train a logistic regression model using some optional optimize algorithm
    # train_x is a mat datatype, each row stands for one sample
    # train_y is mat datatype too, each row is the corresponding label
    # opts is optimize option include step and maximum number of iterations

    # calculate training time
    startTime = time.time()
    train_x=np.asmatrix(train_x)
    train_y=np.asmatrix(train_y)
    numSamples, numFeatures =train_x.shape
    alpha = opts['alpha']; maxIter = opts['maxIter']
    weights = np.ones((numFeatures, 1))
    for k in range(maxIter):
        err = train_y - sigmoid(train_x * weights)
        weights = weights + alpha * train_x.T * err
    print 'Congratulations, training complete! Took %fs!' % (time.time() - startTime)
    return weights


# show your trained logistic regression model only available with 2-D data
def showLogRegres(weights, train_x, train_y):
    # notice: train_x and train_y is mat datatype
    numSamples, numFeatures = train_x.shape
    if numFeatures != 3:
        print "Sorry! I can not draw because the dimension of your data is not 2!"
        return 1

    # draw all samples   
    idx1=np.asarray(train_y)==1
    idx2=np.asarray(train_y)==0
    plt.plot(x[:,1][idx1].T,x[:,2][idx1].T,'or')
    plt.plot(x[:,1][idx2].T,x[:,2][idx2].T,'ob')
    # draw the classify line
    min_x = min(train_x[:, 1])[0, 0]
    max_x = max(train_x[:, 1])[0, 0]
    weights = weights.getA()  # convert mat to array
    y_min_x = float(-weights[0] - weights[1] * min_x) / weights[2]
    y_max_x = float(-weights[0] - weights[1] * max_x) / weights[2]
    plt.plot([min_x, max_x], [y_min_x, y_max_x], '-g')
    plt.xlabel('X1'); plt.ylabel('X2')

# 测试样例
len_samples=500
x=np.random.randn(len_samples,2)
idx1=x[:,0]+x[:,1]>0.5
y=np.zeros((len_samples,1))
y[idx1,0]=1
opt={'alpha':0.1,'maxIter':1000}
x=np.hstack((np.ones((len_samples,1)),x))
x=np.asmatrix(x)
y=np.asmatrix(y)
w=trainLogRegres(x,y,opt)
print w
showLogRegres(w,x,y)

输出如下：

Populating the interactive namespace from numpy and matplotlib
Congratulations, training complete! Took 0.047000s!
[[-17.37216188]
 [ 34.35470115]
 [ 34.98381818]]

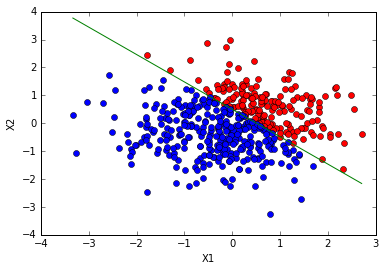
这只是最简单的样例，在实际应用中我们还可以添加惩罚项

[min_{w,c} |w|_2+ Csum_{i=1}^{m} log(1+exp(-y^{(i)}(wcdot x^{(i)}+c))) ]

或者 L_1 范数

[min_{w,c} |w|_1+ Csum_{i=1}^{m} log(1+exp(-y^{(i)}(wcdot x^{(i)}+c))) ]

在样本很稀疏的时候，惩罚项很有用. 另外当样本量很大，我们又极其要求速度的时候，梯度下降法也要改进，换成SGD（stochastic gradient descent ）、拟牛顿法、AGD等等

专注写文二十年，原文首发于公众号，欢迎关注

【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/gasongjian/p/5440519.html