Wikipedia上面的MDCT公式有错？

wikipedia上关于MDCT的公式

http://en.wikipedia.org/wiki/MDCT

As a lapped transform, the MDCT is a bit unusual compared to other Fourier-related transforms in that it has half as many outputs as inputs (instead of the same number). In particular, it is alinear function $F\colon \mathbf{R}^{2N} \to \mathbf{R}^N$ (where R denotes the set of real numbers). The 2N real numbers x₀, ..., x_2N-1 are transformed into the N real numbers X₀, ..., X_N-1 according to the formula:

$X_k = \sum_{n=0}^{2N-1} x_n \cos \left[\frac{\pi}{N} \left(n+\frac{1}{2}+\frac{N}{2}\right) \left(k+\frac{1}{2}\right) \right]$

(The normalization coefficient in front of this transform, here unity, is an arbitrary convention and differs between treatments. Only the product of the normalizations of the MDCT and the IMDCT, below, is constrained.)

Inverse transform [edit]

The inverse MDCT is known as the IMDCT. Because there are different numbers of inputs and outputs, at first glance it might seem that the MDCT should not be invertible. However, perfect invertibility is achieved by adding the overlapped IMDCTs of subsequent overlapping blocks, causing the errors to cancel and the original data to be retrieved; this technique is known as time-domain aliasing cancellation (TDAC).

The IMDCT transforms N real numbers X₀, ..., X_N-1 into 2N real numbers y₀, ..., y_2N-1 according to the formula:

$y_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k \cos \left[\frac{\pi}{N} \left(n+\frac{1}{2}+\frac{N}{2}\right) \left(k+\frac{1}{2}\right) \right]$

(Like for the DCT-IV, an orthogonal transform, the inverse has the same form as the forward transform.)

In the case of a windowed MDCT with the usual window normalization (see below), the normalization coefficient in front of the IMDCT should be multiplied by 2 (i.e., becoming 2/N).

直接实现会发现能量不守恒，编码输入是解码输出的2倍。

参考斯坦福大学JOS的公式

https://ccrma.stanford.edu/~jos/bosse/Modified_Discrete_Cosine_Transform.html

Modified Discrete Cosine Transform (MDCT)

The MDCT is a linear orthogonal lapped transform, based on the idea of time domain aliasing cancellation (TDAC). It was first introduced in [3], and further developed in [4].

MDCT is critically sampled, which means that though it is 50% overlapped, a sequence data represented with MDCT coefficients takes equally much space as the original data. This means, that a single block of IMDCT data does not correspond to the original block, on which the MDCT was performed, but rather to the odd part of that. When subsequent blocks of inverse transformed data are added (still using 50% overlap), the errors introduced by the transform cancels out $\Rightarrow$ TDAC. Thanks to the overlapping feature, the MDCT is very useful for quantization. It effectively removes the otherwise easily detectable blocking artifact between transform blocks. The used definition of MDCT is (a slight modification from [5]) is:

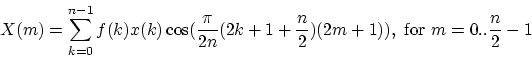$\begin{displaymath} X(m) = \sum_{k=0}^{n-1}{f(k)x(k)\cos(\frac{\pi}{2n}(2k+1+\frac{n}{2})(2m+1))}, \ {\rm for}\ m = 0..\frac{n}{2}-1 \end{displaymath}$

(20)

and the IMDCT:

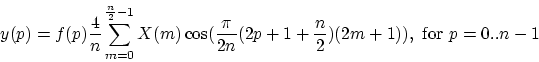$\begin{displaymath} y(p) = f(p)\frac{4}{n}\sum_{m=0}^{\frac{n}{2}-1}{X(m)\cos(\frac{\pi}{2n} (2p+1+\frac{n}{2})(2m+1))},\ {\rm for}\ p=0..n-1 \end{displaymath}$

(21)

注意解码部分4/n比wki的公式多了2倍，就守恒了。

再参考AAC标准13818-7的公式

MDCT

IMDCT：

发现MDCT公式又多乘了2

结论：变换的公式要守恒，但是系数乘在哪里不重要。实际都是归一化的值。

只有比较的相对意义。

但是wiki上对应公式应该守恒处理。