哎,最终还是得接受贝叶斯的宠幸。。。==。。
贝叶斯
preview
emmm。。
先说之前学的概率公式
- 记一个事件A发的概率为P(A),0≤P(A)≤1
- 记事件(A, B)发生的概率为P(A, B),有时也记为P(AB),这表示A, B同时发生的概率;或者记成P(A∩B)
- 记事件A或者B发生的概率为P(A∪B),这里需要注意一下的是,如果A, B不是相互独立的,那么P(A∪B)≠P(A)+P(B)。独立等号就能取到。
独立就是两个集合没有交集。
如果A, B, C是相互独立的,那么有P(ABC)=P(A)P(B)P(C)。这可推广到n种情况,如果事件A1, A2,⋯, An是相互独立的,有如下关系(这个公式我们下面会用到,记住哦)
条件概率:
已知事件B发生的情况下,事件A发生的概率记为P(A|B)
beyes
贝叶斯算法是有监督学习算法,解决的是分类问题,如客户是否流失、是否值得投资、信用等级评定等多分类问题。
但是有限制条件:
以自变量之间的独立(条件特征独立)性和连续变量的正态性假设为前提,就会导致算法精度在某种程度上受影响
推导
分类的核心就是看属于哪类的概率高
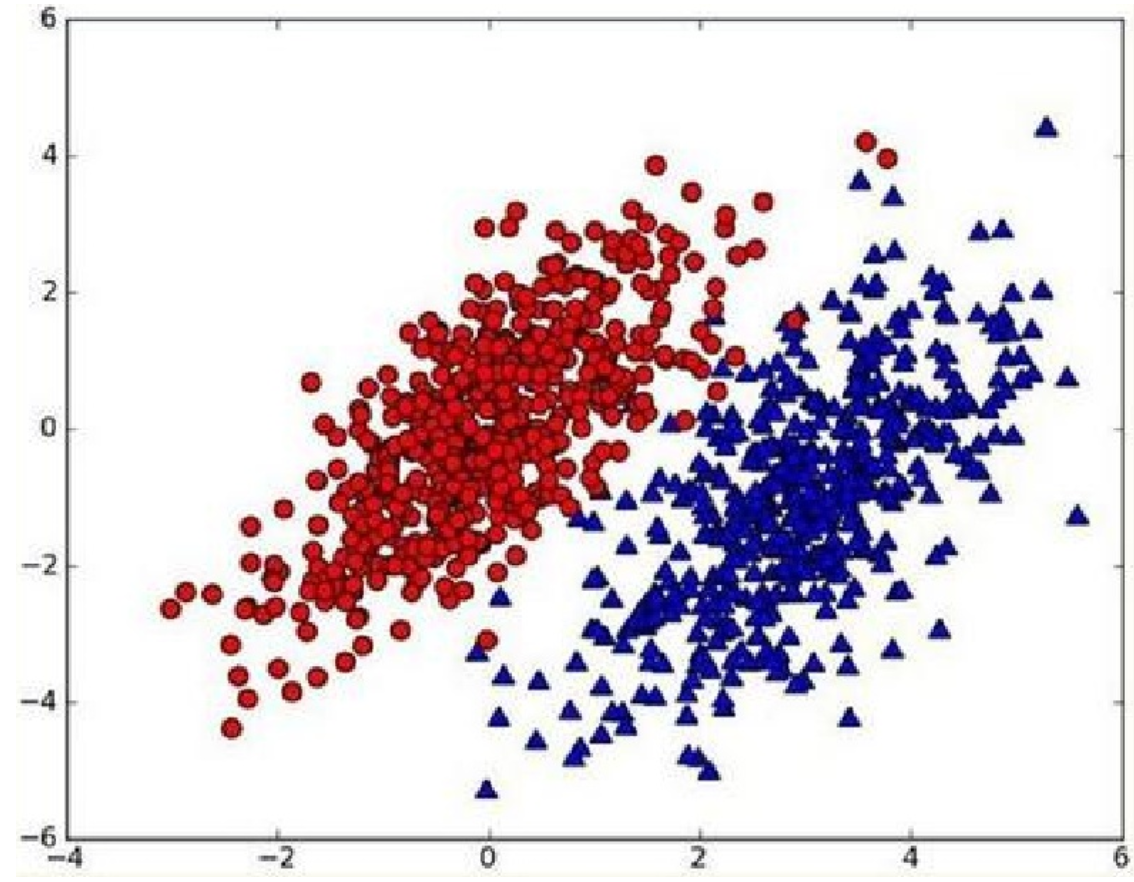
我们现在用(p_1(x,y))表示数据点((x,y))属于类别1(图中红色圆点表示的类别)的概率,用(p_2(x,y))表示数据点((x,y))属于类别2(图中蓝色三角形表示的类别)的概率,那么对于一个新数据点((x_0,y_0))g,可以用下面的规则来判断它的类别:jack cui
如果(p_1(x_0,y_0)>p2(x_0,y_0)),那么类别为1
如果(p_1(x_0,y_0)<p2(x_0,y_0)),那么类别为2
我觉得之前的学习没有对全概率公式好好的理解,没关系可以理解了。
可以图和公式相结合嘛
条件概率公式
这里有一交集图
(P(A | B)=frac{P(A cap B)}{P(B)})
(P(A cap B)=P(A | B) P(B))
(P(A cap B)=P(B | A) P(A))
(P(A | B) P(B)=P(B | A) P(A))
(P(A | B)=frac{P(B | A) P(A)}{P(B)})
全概率公式
参考jack cui
假设A和A'构成了样本空间S

样本空间中还有一个B
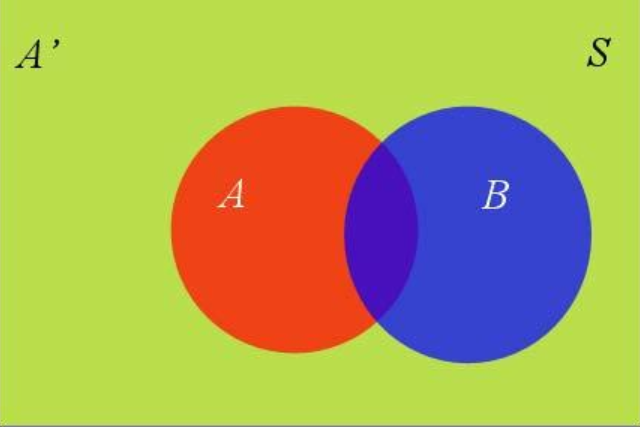
(P(B)=P(B cap A)+Pleft(B cap A^{prime}
ight))
(P(B cap A)=P(B | A) P(A))
(P(B)=P(B | A) P(A)+Pleft(B | A^{prime} ight) Pleft(A^{prime} ight))这就是全概率公式
如果A和A'构成样本空间的一个划分,那么事件B的概率,就等于A和A'的概率分别乘以B对这两个事件的条件概率之和
于是条件概率的另一种写法
(P(A | B)=frac{P(B | A) P(A)}{P(B | A) P(A)+Pleft(B | A^{prime}
ight) Pleft(A^{prime}
ight)})
贝叶斯
就是对条件概率的变形,那么怎么来理解
(P(A | B)=P(A) frac{P(B | A)}{P(B)})
把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。(这里解释的不是很清楚)
后验概率 = 先验概率 x 调整因子
东西看着真的不多
如何理解?
先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。也就是说先测,然后实验进行调整,查看实验之后的效果。
在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。jack cui
这里抓糖的栗子很形象了
在使用该算法的时候,如果不需要知道具体的类别概率,即上面P(H1|E)=0.6,只需要知道所属类别,即来自一号碗,我们有必要计算P(E)这个全概率吗?要知道我们只需要比较 P(H1|E)和P(H2|E)的大小,找到那个最大的概率就可以。既然如此,两者的分母都是相同的,那我们只需要比较分子即可。即比较P(E|H1)P(H1)和P(E|H2)P(H2)的大小,所以为了减少计算量,全概率公式在实际编程中可以不使用。jack cui
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
朴素贝叶斯推断的一些优点:
生成式模型,通过计算概率来进行分类,可以用来处理多分类问题。
对小规模的数据表现很好,适合多分类任务,适合增量式训练,算法也比较简单。
朴素贝叶斯推断的一些缺点:
对输入数据的表达形式很敏感。
由于朴素贝叶斯的“朴素”特点,所以会带来一些准确率上的损失。需要计算先验概率,分类决策存在错误率。
在机器学习的视角下,我们把X理解成“具有的某特征”,把Y理解成“类别标签”(一般机器学习问题中都是X=>特征, Y=>结果对吧)。在最简单的二分类问题(是与否判定)下,我们将Y理解成“属于某类”的标签。于是贝叶斯公式就变形成了下面的样子:han
(P(“属于某类”|“具有某特征”)=frac{P(“具有某特征”|“属于某类”)P(“属于某类”)}{P(“具有某特征”)})
P(“属于某类”∣“具有某特征”)=在已知某样本“具有某特征”的条件下,该样本“属于某类”的概率。所以叫做『后验概率』。
P(“具有某特征”∣“属于某类”)=P(“具有某特征”|“属于某类”)=P(“具有某特征”∣“属于某类”)=在已知某样本“属于某类”的条件下,该样本“具有某特征”的概率。
P(“属于某类”)=P(“属于某类”) =P(“属于某类”)=(在未知某样本具有该“具有某特征”的条件下,)该样本“属于某类”的概率。所以叫做『先验概率』。
P(“具有某特征”)=P(“具有某特征”) =P(“具有某特征”)=(在未知某样本“属于某类”的条件下,)该样本“具有某特征”的概率。han
这个就很好理解了,在没有分类条件下先对特征做一个预判,然后通过分类器之后已知分类了在查看属于某一类别的概率。
而我们二分类问题的最终目的就是要判断P(“属于某类”∣“具有某特征”)是否大于1/2就够了。贝叶斯方法把计算“具有某特征的条件下属于某类”的概率转换成需要计算“属于某类的条件下具有某特征”的概率,而后者获取方法就简单多了,我们只需要找到一些包含已知特征标签的样本,即可进行训练。而样本的类别标签都是明确的,所以贝叶斯方法在机器学习里属于有监督学习方法。
这里再补充一下,一般『先验概率』、『后验概率』是相对出现的,比如P(Y)与P(Y∣X)是关于Y的先验概率与后验概率,P(X)与P(X∣Y)是关于X的先验概率与后验概率。
以垃圾邮件分类为例
举个例子好啦,我们现在要对邮件进行分类,识别垃圾邮件和普通邮件,如果我们选择使用朴素贝叶斯分类器,那目标就是判断P(“垃圾邮件”∣“具有某特征”)是否大于1/2。现在假设我们有垃圾邮件和正常邮件各1万封作为训练集。需要判断以下这个邮件是否属于垃圾邮件:
比如我编的这个
"gwx公司招聘程序员,时薪保底达到1个亿"
也就是判断概率(P(“垃圾邮件”∣“gwx公司招聘程序员,时薪保底达到1个亿”))是否大于1/2。
有木有发现,转换成的这个概率,计算的方法:就是写个计数器,然后+1 +1 +1统计出所有垃圾邮件和正常邮件中出现这句话的次数啊!!!好,具体点说:
$ =frac{垃圾邮件中出现这句话的次数}{垃圾邮件中出现这句话的次数+正常邮件中出现这句话的次数}$
但是发邮件不可能会有那么多一样的句子,不要低估人类的智商嗷
训练集是有限的,而句子的可能性则是无限的。所以覆盖所有句子可能性的训练集是不存在的。
所以解决方法是?
对啦!句子的可能性无限,但是词语就那么些!!汉语常用字2500个,常用词语也就56000个(你终于明白小学语文老师的用心良苦了)。按人们的经验理解,两句话意思相近并不强求非得每个字、词语都一样。比如“gwx公司招聘程序员,时薪达到1个亿”,这句话就比之前那句话少了“(保底)”这个词,但是意思基本一样。如果把这些情况也考虑进来,那样本数量就会增加,这就方便我们计算了。
于是,我们可以不拿句子作为特征,而是拿句子里面的词语(组合)作为特征去考虑。比如“招聘”可以作为一个单独的词语,“时薪”也可以作为一个单独的词语等等。
于是就变成了(“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”)
于是你接触到了中文NLP中,最最最重要的技术之一:分词!!!也就是把一整句话拆分成更细粒度的词语来进行表示。咳咳,另外,分词之后去除标点符号、数字甚至无关成分(停用词)是特征预处理中的一项技术。
我们观察(“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”),这可以理解成一个向量:向量的每一维度都表示着该特征词在文本中的特定位置存在。这种将特征拆分成更小的单元,依据这些更灵活、更细粒度的特征进行判断的思维方式,在自然语言处理与机器学习中都是非常常见又有效的。
(P(“垃圾邮件”|(“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”))=frac{P((“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”)|“垃圾邮件”)P(“垃圾邮件”)}{P(“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”)})
(P(“正常邮件”|(“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”))=frac{P((“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”)|“正常邮件”)P(“正常邮件”)}{P(“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”)})
贝叶斯的前提是条件独立的,因此可以拆分
使用F代表垃圾邮件,A代表正常邮件
(P(“gwx”,“公司”,“招聘”,“程序员”,“时薪”,“保底”,“达到”,“1个亿”)∣F) =P(“gwx”∣F)×P(“公司”∣F)×P(“招聘”∣F)×P(“程序员”∣F)×P(“时薪”∣F)×P(“保底”∣F)×P(“达到”∣F)×P(“1个亿”∣F))
正常邮件同理
统计次数非常方便,而且样本数量足够大,算出来的概率比较接近真实。于是垃圾邮件识别的问题就可解了。
加上条件独立假设的贝叶斯方法就是朴素贝叶斯方法(Naive Bayes)。 Naive的发音是“乃一污”,意思是“朴素的”、“幼稚的”、“蠢蠢的”。咳咳,也就是说,大神们取名说该方法是一种比较萌蠢的方法,hahahah~
但是这个句子中还是有停用词,需要选择关键词(关键词有时候可以代替一整个邮件,剔除停用词
贝叶斯公式 + 条件独立假设 = 朴素贝叶斯方法