今天学了一下树状数组。
如果给定一个数组,要你求里面所有数的和,一般都会想到累加。但是当那个数组很大的时候,累加就显得太耗时了,时间复杂度为O(n),并且采用累加的方法 还有一个局限,那就是,当修改掉数组中的元素后,仍然要你求数组中某段元素的和,就显得麻烦了。所以我们就要用到树状数组,他的时间复杂度为 O(lgn),相比之下就快得多。下面就讲一下什么是树状数组:
一般讲到树状数组都会少不了下面这个图:
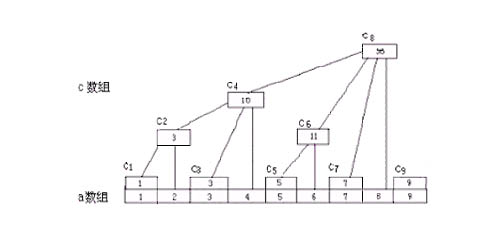
下面来分析一下上面那个图看能得出什么规律:
据图可 知:
令这棵树的结点编号为C1,C2...Cn。令每个结点的值为这棵树的值的总和,那么容易发现:
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
...
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16
这里有一个有趣的性质:
设节点编号为x,那么这个节点管辖的区间为2^k(其中k为x二进制末尾0的个数)个元素。因为这个区间最后一个元素必然为Ax,
所以很明显:Cn = A(n – 2^k + 1) + ... + An
那么,如何求 2^k 呢?求法如下:
int lowbit(int x)
{
return x&(-x);
}
lowbit()的返回值就是 2^k 次方的值。
求出来 2^k 之后,数组 c 的值就都出来了,接下来我们要求数组中所有元素的和。
(二)求数组的和的算法如下:
(1)首先,令sum=0,转向第二步;
(2)接下来判断,如果 n>0 的话,就令sum=sum+cn转向第三步,否则的话,终止算法,返回 sum 的值;
(3)n=n - lowbit(n)(将n的二进制表示的最后一个零删掉),回第二步。
代码实现:
int sum(int x) { int s=0,i; for(i=x; i; i-=lowbit(i))s+=a[i]; return s; }
(三)当数组中的元素有变更时,树状数组就发挥它的优势了,算法如下(修改为给某个节点 i 加上 x ):
(1)当 i<=n 时,执行下一步;否则的话,算法结束;
(2)ci=ci+x ,i=i+lowbit(i)(在 i 的二进制表示的最后加零),返回第一步。
代码实现:
1 void add(int x,int c) 2 { 3 int i; 4 for(i=x; i<=n; i+=lowbit(i))a[i]+=c; 5 }