
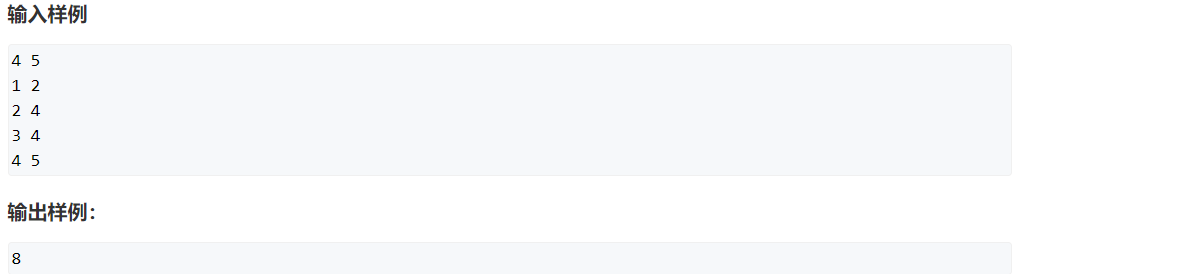
01背包问题是每件物品要么用0次,要么用1次,最多只用一次
dp[i][j]表示只从前i个物品中选,总体积<=j的选法的最大价值。

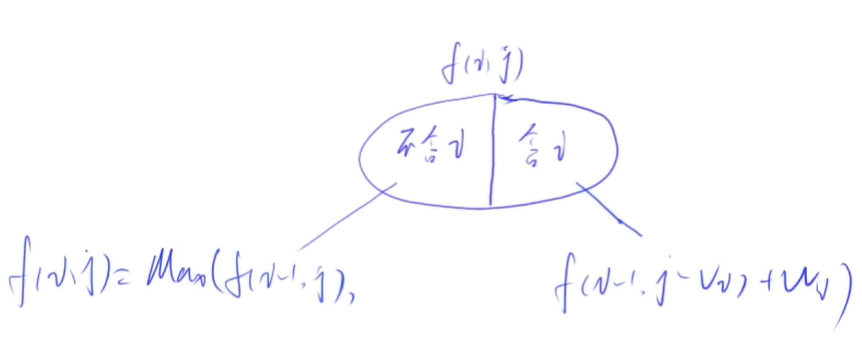
二维做法
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 1010; 4 int dp[N][N]; 5 int v[N], w[N]; //v是每件物品的体积,w是每件物品的价值 6 int main() { 7 int n, m; //n是物品个数,m是背包容量 8 cin >> n >> m; 9 for (int i = 1; i <= n; i++) { 10 cin >> v[i] >> w[i]; 11 } 12 //初始化dp[0][0~m]一件物品都没有选,所以是0 13 for (int i = 1; i <= n; i++) { //然后从第一件物品开始 14 for (int j = 0; j <= m; j++) { //枚举体积 15 //不含i的情况是一定存在的 16 dp[i][j] = dp[i - 1][j]; 17 //但是含i的情况是有条件的 18 if (j >= v[i]) { //只有能装下时才有这种情况 19 dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]); 20 } 21 } 22 } 23 /*for (int i = 1; i <= n; i++) { 24 for (int j = 0; j <= m; j++) { 25 cout << dp[i][j] << " "; 26 } 27 cout << endl; 28 }*/ 29 cout << dp[n][m] << endl; 30 return 0; 31 }
输出中间变量
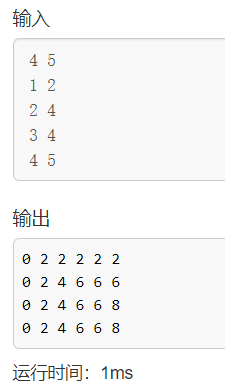
然后我们将二维转化为一维
能转换为一维是由两个原因决定的
因为dp[i][]这一层只用到了dp[i - 1][]这一层,所以就可以运用滚动数组的思想
然后我们又发现了另外一个问题,关于j,我们用到的一个是j一个是j - v[i],都是<= j的
所以我们就改为用一维数组来算
二维优化到一维,内层循环需要逆序
我们可以对比一下这两个式子:
dp[i][w]=max{dp[i-1][w],dp[i-1][w-wi]+vi}
f[w]=max{f[w], f[w-wi]+vi}
可以发现, 在一维递归式里, 要求f[w-wi]+vi 这部分 代替 dp[i-1][w-wi]+vi这部分
我们现在又只有一维数组. 这就要保证, 在第i次外循环时, 调用的f[w-wi]实际上是基于第i-1次循环得到的值.
而逆序保证了, 对于f[w], 它要调用的f[w-wi]一定是第i层循环还没有更新过的, 换言之, f[w-wi]只有可能是第i-1层存储的数据.
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 1010; 4 int dp[N]; 5 int v[N], w[N]; //v是每件物品的体积,w是每件物品的价值 6 int main() { 7 int n, m; //n是物品个数,m是背包容量 8 cin >> n >> m; 9 for (int i = 1; i <= n; i++) { 10 cin >> v[i] >> w[i]; 11 } 12 for (int i = 1; i <= n; i++) { //然后从第一件物品开始 13 for (int j = m; j >= v[i]; j--) { //枚举体积 14 dp[j] = max(dp[j], dp[j - v[i]] + w[i]); 15 //cout << "i: " << i << " j: " << j << " dp[j]: " << dp[j] << endl; 16 //dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]); 17 //第i层算的dp[j]一定是dp[i][j], j - v[i]是严格小于j的 18 //然后j是从小到大枚举的,所以说我们在算dp[j]的时候 19 //dp[j - v[i]]在第i层已经被计算过了 20 21 //所以我们把体积从大到小枚举 22 //这样的话,我们就保证了由于j - v[i] < j 23 //所以我们在算dp[j]时,dp[j - v[i]]还没有被更新过 24 //那么它存的就是第i - 1层的j - v[i] 25 } 26 } 27 cout << dp[m] << endl; 28 return 0; 29 }