Splay算法详解
本篇随笔浅谈一下算法竞赛中的(Splay)算法。
Splay的概念
Splay在我看来应该算作一种算法而非数据结构。无论是Treap,AVL,SBT,替罪羊树还是Splay其实都应该算作算法,因为它们都在解决一种数据结构存在的问题:二叉搜索树(BST)。
对于二叉搜索树和Treap(平衡树概念)不了解的,可以移步下面两篇博客:
有了前置知识,我们可以发现问题的根源在于(BST)在数据极端的情况下会退化成链。而什么Treap啊,AVL啊,SBT啊,Splay啊,替罪羊树啊都是在干一件事情:如何让这棵树尽可能平衡,不要退化成链。
有个叫做Tarjan的大佬YY出了Splay这种算法。
Splay的实现方式
Treap的实现原理在于为所有节点附加一个键值。这个键值按堆的形式排序。让整个数据结构在节点权值上是BST,但在优先级(键值)上却是一个堆。
但Splay的实现方式是对节点的序号进行重构,从而达到平衡树要求的标准。
splay操作
splay操作是指将一个点一直上旋,知道某个指定点。默认是根节点。
Splay的精髓在于旋转,这已经是不争的事实了。
如果对于树的旋转这个知识点有些不明白,请移步Treap的博客:
相比于Treap只有单旋这一种旋转方式,Splay的优秀之处在于它有着4种旋转方式:单旋和双旋。
什么是双旋?为什么要双旋?
双旋的适用范围在于:祖父、父亲和儿子节点连成一条线。
就像这样:
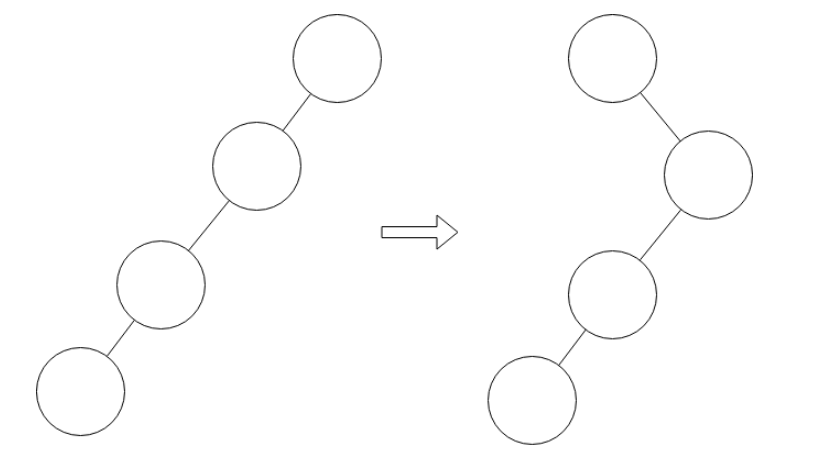
如果这样的结构不去双旋而简单粗暴地用两次单旋(先将需要旋转的节点上旋,再转他的父亲)来解决,最后造成的结果就像是右边的样子(自己手画模拟一下两次单旋即可发现)。我们发现,左侧的树是四层,右侧的树仍然是四层:对于复杂度来讲,没有任何优化。因为我们的平衡树是尽量把复杂度变成(log)级别的。
那么,我们就需要使用双旋。双旋的操作方式是:先将父节点上旋,再将需要旋转的节点上旋。别看这个双旋只是改变了其旋转顺序,但是可是大有文章,经过这样的旋转策略,最终的旋转结果就变成了这样:
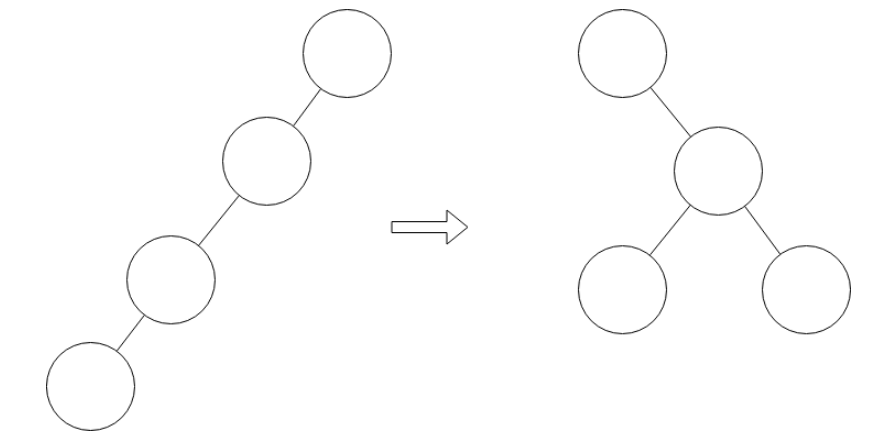
嗯,不错,少了一层,看起来很平衡。
所以,我们的Splay的精华是Splay操作,也就是把某个节点一直转到根节点,顺道改变整棵树的形态。具体实现方式是:如果当前节点的父亲节点就是根节点或者自己、父亲、祖父不在一条直线上,就单旋;如果自己、父亲、祖父正好在同一条直线上,那么就双旋:双旋的策略是:先转父亲后转自己。
所以我们有四种旋转方式:单旋左旋,单旋右旋,双旋左旋,双旋右旋。
这也是Splay的基本操作。
Splay和Treap在旋转上的区别
学过Treap的小伙伴(包括我)都在觉得Splay的单旋和Treap的左右旋好像是一样的。但是实际上它们却有所不同。在本蒟蒻的理解上,这种不同体现在“对象”上。
Treap的旋转是将儿子节点旋到自己的位置。左旋是把右儿子转到自己的位置,右旋是把左儿子转到自己的位置。
但是Splay的旋转则是将自己转到父亲节点的位置,虽然形式上都是上旋,但是作用对象是不一样的。
Splay的代码实现
一般来讲,Splay支持的操作和Treap是差不多的。其实所有的平衡树都是这种操作。动态插入删除,然后去动态查询第k大、数的排名、前驱、后继等等。因为平衡树的本质是BST,所以BST所拥有的性质,Splay全都可以支持和维护。
就拿洛谷的例题来讲吧:P3369的模板。
前置信息
前置信息包括三个函数:maintain函数(来维护节点的size,后期统计排名用),get函数(确认当前节点是它爹的左儿子还是右儿子,旋转要用)以及find函数(在树中找到某个值的节点位置)
void maintain(int x)
{
size[x]=cnt[x]+size[ch[x][0]]+size[ch[x][1]];
}
int find(int x)
{
int pos=root;
while(val[pos]!=x)
pos=ch[pos][x>val[pos]];
return pos;
}
int get(int x)
{
int f=fa[x];
return ch[f][1]==x;
}
代码很简单,应该一看就能懂。
旋转&Splay操作
上面的Splay的实现原理就在讲旋转和Splay操作的原理。依照上面讲的模拟即可得到下面的模板:
void rotate(int x)
{
int y=fa[x],z=fa[y];
int k=get(x);//k表示x是y的什么儿子
ch[y][k]=ch[x][k^1],fa[ch[y][k]]=y;
ch[x][k^1]=y,fa[y]=x,fa[x]=z;
if(z)
ch[z][ch[z][1]==y]=x;
maintain(y),maintain(x);
}
void splay(int x,int &goal)
{
int f=fa[goal];
while(fa[x]!=f)
{
if(fa[fa[x]]!=f)
rotate(get(x)==get(fa[x])?fa[x]:x);
rotate(x);
}
goal=x;
}
插入
插入的时候需要一个动态开点。也就是用到哪开到哪,所以一开始首先要判整棵树是不是空的。然后再去进行插入。插入的时候要注意:因为有些数可以重复出现。所以当我们在原树中找到与插入节点完全相同的节点之后,不用去插入,直接把计数变量+1就可。
如果这是一个全新的节点,那么它一定是个叶子。所以如果我们没在原树中找到这个节点的话,就得用动态开点把点加进去。
动态开点不太会的小伙伴走这边:
插入要注意两点:第一点是maintain,也就是统计节点的大小。第二点是Splay,每次插入和删除之后都要Splay,来维护树的形态。这也是Splay算法的精髓所在,一定不要忽略。这两种操作应该maintain在前,splay在后,因为在进入splay之前要保证当前状态下所有节点的信息都是对的,才能保证Splay之后所有节点的信息也都是对的。
插入代码:
void insert(int x)
{
if(!root)
{
++tot;
root=tot;
val[root]=x;
cnt[root]=1;
maintain(root);
return;
}
int pos,f;
pos=f=root;
while(pos && val[pos]!=x)
f=pos,pos=ch[pos][x>val[pos]];
if(!pos)
{
++tot;
cnt[tot]=1;
val[tot]=x;
fa[tot]=f;
ch[f][x>val[f]]=tot;
maintain(tot);
splay(tot,root);
return;
}
++cnt[pos];
maintain(pos);
splay(pos,root);
}
删除
删除的操作其实和Treap的有些像,但是又有些不同。作为一个树中节点来讲,尤其是一个BST的节点,我们肯定不能直接上来就暴力删掉这个节点,否则无法维护BST的性质。为了解决这个问题,我们选择把节点直接Splay转到根节点,这样的话,直接删根对左右子树是无影响的,直接合并就好。
但是要分几种情况讨论:(Splay之后)
首先,如果这个点有很多数,但是我们只删一个,所以直接cnt-1就可,其他不用变。
如果只有一个,那么就要删除,但是删除之后谁来当根节点呢?这又有三种情况可以讨论:根节点只有左儿子,根节点只有右儿子,根节点儿女双全。
前两种只能给唯一的儿子。如果儿女双全,就得在删掉当前根节点后再找一个根节点,但是问题来了,新的根节点到底是用左儿子合适还是用右儿子合适?
都不合适。根据BST的性质,因为左子树都比当前节点小,右子树都比当前节点大,所以我们选择根节点左子树中最大的点作为根节点(就是根节点向左,然后一直向右到头)。
别忘了Splay维护和maintain更新。
代码:
void del(int x)
{
int pos=find(x);
splay(pos,root);
if(cnt[root]>1)
{
cnt[root]--;
maintain(root);
return;
}
if((!ch[root][0])&&(!ch[root][1]))
root=0;
else if(!ch[root][0])
root=ch[root][1],fa[root]=0;
else if(!ch[root][1])
root=ch[root][0],fa[root]=0;
else
{
pos=ch[root][0];
while(ch[pos][1])
pos=ch[pos][1];
splay(pos,ch[root][0]);
ch[pos][1]=ch[root][1];
fa[ch[root][1]]=pos,fa[pos]=0;
maintain(pos);
root=pos;
}
}
查询排名
当然可以用BST的性质来遍历树计算排名。但是好笨的样子。
我们会Splay啊,直接把要查的节点Splay上去,然后直接调用其左子树的size+1不就可以了嘛!
int rank(int x)
{
int pos=find(x);
splay(pos,root);
return size[ch[root][0]]+1;
}
查询第k大
int kth(int x)
{
int pos=root;
while(1)
{
if(x<=size[ch[pos][0]])
pos=ch[pos][0];
else
{
x-=(size[ch[pos][0]]+cnt[pos]);
if(x<=0)
{
splay(pos,root);
return val[pos];
}
pos=ch[pos][1];
}
}
}
查询前驱/后继
前驱和后继的定义已经给出。我们惊喜地发现和BST的性质真的是无比的契合。
所以我们直接用BST查就可以,任何平衡树算法都是一样的。
代码:
int pre(int x)//前驱
{
int ans;
int pos=root;
while(pos)
{
if(x>val[pos])
{
ans=val[pos];
pos=ch[pos][1];
}
else
pos=ch[pos][0];
}
return ans;
}
int nxt(int x)//后继
{
int ans;
int pos=root;
while(pos)
{
if(x<val[pos])
{
ans=val[pos];
pos=ch[pos][0];
}
else
pos=ch[pos][1];
}
return ans;
}