【题型一】直线分割平面
在一个平面上有一个圆和n条直线,这些直线中每一条在圆内同其他直线相交,假设没有3条直线相交于一点,试问这些直线将圆分成多少区域。
分析: 
当添加第N条,为了使平面最多, 则第N条直线要与前面的N-1条直线都相交,且没有任何三条直线相交一个点。
则添加第N条直线会多N-1个交点。由于每增加N个交点,就增加N+1个平面,所以添加第N条直线来会在之前的基础上增加N个平面,用F[i]表示i条直线能把平面切分成的个数。
F[1]=2;
F[n]=F[n-1]+n;
递推的F[n]=1+n*(n+1)/2
【题型二】平面分割空间(HDU 1290)
分析:由二维的分割问题可知,平面分割与线之间的交点有关,即交点决定射线和线段的条数,从而决定新增的区域数。
试想在三维中则是否与平面的交线有关呢?
当有n-1个平面时,分割的空间数为f(n-1)。
要有最多的空间数,则第n个平面需与前n-1个平面相交,且不能有共同的交线。
即最多有n-1 条交线。而这n-1条交线把第n个平面最多分割成g(n-1)个区域。
(g(n)为(1)中的直线分平面的个数)此平面将原有的空间一分为二,
则最多增加g(n-1)个空间。
故:f(n)=f(n-1)+g(n-1) ( ps: g(n)=n(n+1)/2+1 )
f(n-1)=f(n-2)+g(n-2)
……
f(2)=f(1)+g(1)
因为,f(1)=g(1)=2
所以,f(n)=2+(1*2+2*3+3*4+……+(n-1)n)/2+(n-1)
=[ (1^2+2^2+3^2+4^2+……+n^2) - (1+2+3+……+n ) ]/2 + n+ 1
=(n^3+5n)/6+1
【题型三】折线分割平面(HDU 2050)
平面上有n条折线,问这些折线最多能将平面分割成多少块? 
分析先以问题一作为基础,
再看每次增加两条相互平行的直线的情况。
根据题型一分析可以知道
当第N次添加时,前面已经有2N-2条直线了,所以第N次添加时,第2N-1条直线和第2N条直线都各能增加2*(n-1)+1 个平面。
所以第N次添加增加的面数是2[2(n-1) + 1] = 4n - 2 个。因此,总面数应该是
1 + 4n(n+1)/2 - 2n = 2n2 + 1
如果把每次加进来的平行边让它们一头相交

则平面1、3已经合为一个面,因此,每一组平行线相交后,就会较少一个面,
所以所求就是平行线分割平面数减去N,为2n2 -n + 1.
利用上述总结公式f(n)=2n2 -n + 1
【题型四】圆形划分区域
题目:设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,
且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
分析:当n-1个圆时,区域数为f(n-1).那么第n个圆就必须与前n-1个圆相交,
则第n个圆被分为2(n-1)段线段,增加了2(n-1)个区域。
故: f(n)=f(n-1)+2*(n-1)
f(n-1)=f(n-2)+2*(n-2)
......
f(2)=f(1)+2*1
因为,f(1)=2
所以,f(n)=n^2-n+2
【拓展】
①:
说起佐罗,大家首先想到的除了他脸上的面具,恐怕还有他每次刻下的“Z”字。我们知道,一个“Z”可以把平面分为2部分,两个“Z”可以把平面分为12部分,那么,现在的问题是:如果平面上有n个“Z”,平面最多可以分割为几部分呢?
说明1:“Z”的两端应看成射线
说明2:“Z”的两条射线规定为平行的
分析:
设f(n)表示n个z字型折线至多平面划分数。
现在增加一条边a,和3n条线都相交,增加3n+1个区域。
再增加一条边b,与a平行,同样增加3n+1个区域。
最后增加一条边c,与已有的边都相交,增加3n+3个区域。又因为要与a,b形成锯齿形,所以又减去2*2个区域
所以得出递推式 f(n)=f(n-1)+9*(n-1)+1.
利用上述递推式总结为f(n)=9*n*(n-1)/2+n+1.
②(HDU 1249):
用N个三角形最多可以把平面分成几个区域?
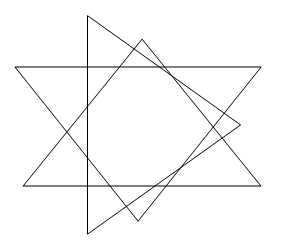
这时我们来回顾一下前3种情况
n 1 2 3
f(n) 2 8 20
不知道你们为了得到尽可能多的区域是如何去画这些三角形的,或许你会发现,画第n个三角形的时候,该三角形的一条边会穿过2(n-1)条边,这时,我们再来看看前3种情况,就会发现8=2+(2+2+2),20=8+(4+4+4),这增加的正好是3倍穿过的边数,即3*2(n-1)
于是,我们得到f(n)=f(n-1)+3*2(n-1)=f(n-1)+6(n-1)。
这样我们便可以利用累加法求出f(n)=3*n*n-3*n+2。
其实,对此类题都有一固定做法:
对于二维空间来说:f(x)=ax^2+bx+c;
对于三维空间:f(x)=ax^3+bx^2+cx+d;
只要通过带入x的值,求出a、b、c、d这些未知量即可得到公式。
以上内容均摘录自网上
