前言
本篇博客的字符串下标是从1开始的。
引入
给出两个字符串(A,B),询问(B)是否是(A)的子串。
对于以上问题,我们有一个比较暴力的想法,就是一位一位去配对呀。
给出代码:
int Check(){
for(int i=1;i+M-1<=N;i++){
int j=0;
while(j<M&&A[i+j]==B[j+1])j++;
if(j==M)return 1;
}
return 0;
}
但是显然,这个算法并不太优秀。(可以被卡到(O(Ncdot M)))
(尽管对于大多数题够用了)
引入KMP算法。
P1(定义)
对于A=ababababc,B=ababc的例子,我们观察一下Check函数的过程。
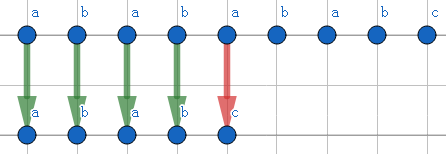
第一步,两个字符串可以配对到abab(绿边),直到遇到a与c,发现不能配对(红边)。此处贡献4步。
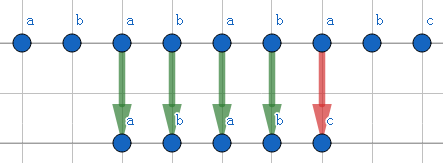
第二步,两个字符串再次配对到abab,并再次不能配对,贡献4步。
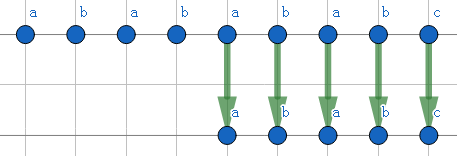
第三步,两个字符串完全配对,出解,并再次贡献4步。
注:以上贡献次数指除开了遍历了一次A串的步数。
考虑对以上过程优化。
可以发现,我们在第一步失配时,完全可以直接跳到下图的情况。
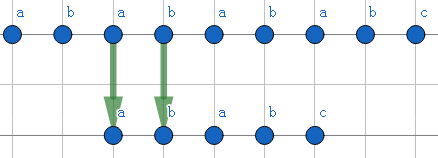
即我们的j的下标完全可以从4跳到2(失配前的下标)。
即我们如果能够处理出关于B串的一个数组,使得我们可以进行刚才的跳跃操作就好了。
于是乎,我们定义一个 (Next) 数组:
(Next[i])表示的是满足如下条件的一个串的末端下标。
该串是(B[1])$B[i]$这个串的后缀,也是$B[1]$(B[i])这个串的前缀,并且是满足以上两个条件的串中长度最长的串。
(限制(Next[i])值不能为(i),即跳跃操作至少往前跳1格)。
(语言表达不好,不如来看看例子)
还是之前那个例子:(B=ababc)
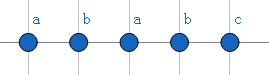
那么在处理(Next[4])时(即子串abab时),我们暴力的过程如下:
找出该子串的所有后缀(不算自己):
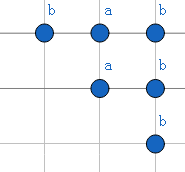
然后找出其所有前缀(同样不算自己):
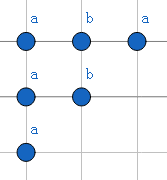
发现ab为两次查找均出现过串中最长的串,故满足要求,即(Next[4])的值就为(2)。
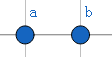
对于该例子(B=ababc)的所有(Next)值就是:
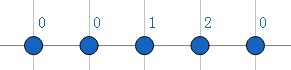
失配时跳跃情况如下:
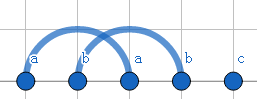
P2(初始化)
那么我们应该如何求出(Next)数组呢?
考虑求解(Next[i])时(假设(Next[1])~(Next[i-1])都求好了),我们如何用之前的状态转移。设之前的状态长这样:紫点与绿点是完全相等的两个子串,弧线表示(Next[i-1]),我们现在要求红点的(Next)值。
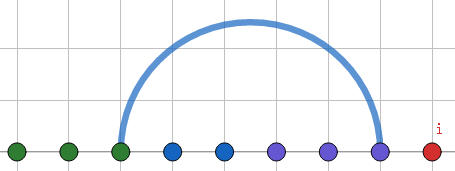
那么我们只需要去比较一下下图的红点与橙点是否相等就行了:
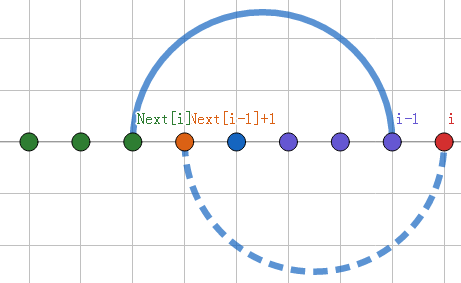
如果相等,那么 (Next[i]) 就等于 (Next[i-1]+1) 。
否则,我们就去访问下标为 (Next[Next[i]]+1) 的点再次比较,直到不能比较为止。
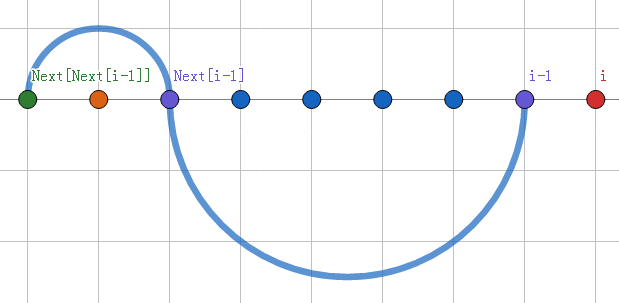
因为这样的话,同样也满足(Next)数组的性质:
(B[i-1]=B[Next[i-1]]=B[Next[Next[i-1]]]=...=B[Next[....]])
而最终求得的那个前缀,同样会是(B[1])~(B[i])的某个后缀。
P3(求解)
基于P1与P2的内容,P3就比较好理解了。
我们在最初那个暴力Check上改改就行了。
如果失配了,回到一个满足条件的Next[j]就行了。
原理呢,其实和P2初始化部分是一样的。
实在不懂的话,那还是举个例子吧。
对于A=ababababc,B=ababc时,我们用KMP算法来做一下。

发现a和c失配,现在(j=4),考虑让(j=Next[j]),更改后(j=2),贡献为4。

继续往后,发现失配,现在(j=4),再次让(j=Next[j]),更改后(j=2),贡献为3。

情况变化成下图:

最后出解,贡献为3。

虽然只比暴力的总贡献少两步,但在某些恶意卡暴力的题中,还是得用KMP算法。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=1000005;
int K,N,M,Next[MAXN],Ans;
char A[MAXN],B[MAXN];
void Prepare(){
for(int i=2;i<=M;i++){//注意从2开始.
int j=Next[i-1];
if(B[j+1]!=B[i]&&j>0)j=Next[j];
if(B[i]==B[j+1])j++;//判等于0的情况.
Next[i]=j;
}
}
int Find(){
int i=1,j=0;
for(int i=1,j=0;i<=N;i++){
while(j&&A[i]!=B[j+1])j=Next[j];
if(A[i]==B[j+1])j++;
if(j==M){
Ans++;
j=Next[j];
}
}
}
int main(){
scanf("%d",&K);
while(K--){
scanf("%s%s",B+1,A+1);
N=strlen(A+1);M=strlen(B+1);
Ans=0;Prepare();Find();
printf("%d
",Ans);
}
}
/*
ababababc
ababc
*/
后记
关于KMP算法的时间复杂度:
Q:求解(Next)时,(j)指针难道不会跳很多次吗,这个复杂度难道不是(O(M^2))吗?
A:其实可以发现,每次j=Next[j]的操作都会使当前的(Next)值比上一次的(Next)值小。
画出(Next)的函数图像如下:
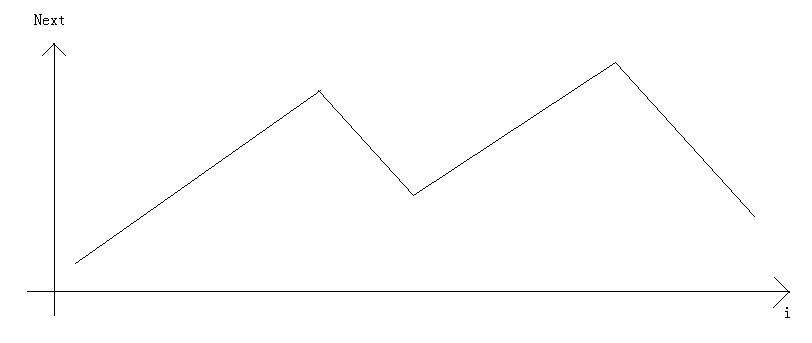
那么对于满足(Next[i]>Next[i-1])的(Next[i])肯定都是在(O(1))的时间里出解的。
而那些(Next[i]<Next[i-1])的(Next[i])总跳跃次数并不会超过(M)。
因为(Next)函数的值域是在(M)以内的,而且一次上升的差距肯定为1。
(即若(Next[i]>Next[i-1]),那么有(Next[i]=Next[i-1]+1))
而一次回跳至少跳1格,故总回跳次数是不会超过(M)次的。
Q:求解时每次失配,(j)指针最多还是会跳(M)次嘛,看似还是可以卡到(O(Ncdot M))嘛。
A:实则不然,指针(j)每次都是和(i)一起变化的,只有在(i)加1时,(j)才有可能跟着加1。这样的话,(j)失配往回跳的总次数是不会超过(N)次的(每次跳都至少跳1格)。故KMP算法的时间复杂度是十分优秀的(O(N)+O(M)=O(N+M))啦。