1、我们说矩阵的逆,是针对方阵(见下面wiki的定义)
给定一个 n 阶方阵  ,若存在一 n 阶方阵
,若存在一 n 阶方阵 ,使得
,使得 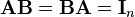 ,其中
,其中 为 n 阶单位矩阵,则称
为 n 阶单位矩阵,则称 是可逆的,且
是可逆的,且  是
是  的逆矩阵,记作
的逆矩阵,记作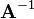 。
。
若方阵 的逆阵存在,则称
的逆阵存在,则称 为非奇异方阵或可逆方阵
为非奇异方阵或可逆方阵
(http://zh.wikipedia.org/wiki/%E9%80%86%E7%9F%A9%E9%98%B5)
性质:
(1)矩阵的逆是唯一的
(2)如果A 可逆,数λ≠ 0 ,那么 ( ![]() A)-1=
A)-1= ![]() A-1 ;
A-1 ;
(3)如果A 可逆,那么,A T 也可逆,而且 ( AT )-1=( A-1)T ;
(4)如果A ,B 皆可逆,那么 AB 也可逆,且(AB) -1=B-1A-1
矩阵的初等变换
定义 下面三种变换称为矩阵的初等行变换:
1. 互换两行(记 ![]() );
);
2. 以数 ![]()
![]() 乘以某一行(记
乘以某一行(记![]() );
);
3. 把某一行的 ![]() 倍加到另一行上(记
倍加到另一行上(记![]() )
)
若将定义中的“行”换成“列”,则称之为初等列变换,初等行变换和初等列变换统称为初等变换。
定义 若矩阵 ![]() 经有限次初等行变换变成矩阵
经有限次初等行变换变成矩阵![]() ,则称
,则称![]() 与
与![]() 行等价,记
行等价,记![]() ;
;
若矩阵 ![]() 经有限次初等列变换变成矩阵
经有限次初等列变换变成矩阵![]() ,则称
,则称![]() 与
与![]() 列等价,记
列等价,记![]() ;
;
若矩阵 ![]() 经有限次初等变换变成矩阵
经有限次初等变换变成矩阵![]() ,则称
,则称![]() 与
与![]() 等价,记
等价,记![]() 。
。
阶梯形矩阵定义:一个矩阵中每个非零行的首元素(指该行第一个非零元素)出现在上一行首元素的右边,同时,没有一个非零行出现在全零行的下方,这样的矩阵称为阶梯形矩阵
定理:任何一个矩阵 A 都行等价于一个阶梯形矩阵。
简化阶梯形矩阵定义:一个阶梯形矩阵,如果它的每一非零行的首元素是 1 ,且首元素所在列的其余元素全是零,就称为简化阶梯形矩阵。
定理:任何一个矩阵行等价于一个简化阶梯形矩阵。
定理:任何一个非零矩阵 A ∈Mm × n (F )可经过有限次初等变换化为下面形似的矩阵:  =
= ![]() ,
,
1 ≤r ≤min(m,n), 它称为矩阵A 的标准形
推论:任意一个非零矩阵 A ∈Mm × n (F ) ,一定存在m 阶可逆阵P 和n 阶可逆阵Q ,使
PAQ= ![]() ,其中 ,
,其中 , ![]() 是A 的标准形。
是A 的标准形。
推论:设A ,B 均是m*n的矩阵,A 与B 等价的充要条件是 AB 有相同的标准形。
定理:设A 为n 阶矩阵,下列叙述等价:
1 、 A 是可逆阵;
2 、 A 行等价于单位阵 E ;
3 、A 可表示为一些初等矩阵的乘积。
参考:http://web.tongji.edu.cn/~math/xxds/kcja/kcja_a/kcja_a.htm(第1、2、3节)