第一次算法作业共十题,包括简单的定积分求值、不等式证明、算法原理分析、搜索有序表、八皇后拓展、素数判定,主要是概率算法的掌握。
对某些问题确定性算法求解起来时间很长,而概率算法则能相对容易求得正确结果,如快速排序随机划分问题、八皇后求解问题、判断大整数是否伪素数问题。
概率算法分为数字算法、Mente Carlo算法、Las Vegas算法、Sherwood算法,其中MC算法不管正确与否总是给出一个结果,LV算法不返回错误的答案但有时根本找不到答案,MC和LV算法找到正确结果的概率正比于算法执行时间。Sherwood算法总是给出正确的答案,通常可以消除好坏实例之间的差别,用于当算法解决问题的平均时间远小于最坏时间。
作业1,2,3均为数字概率算法。作业5估计集合X的势的概率算法。作业7是sherwood算法搜索有序数组问题。作业9求n=12~20最优StepVegas值利用LV算法和确定性回溯算法相结合。作业10用MC算法求100~10000以内错误素数(即强伪素数)的比例。
其中:
作业5当n足够大(2^31)时,估计的n与实际n相差太大。尝试提高随机数的范围但错误率仍然很大,估计是算法本身不合理的问题。
作业7有序表通过两个序列确定, 分别是val和ptr,如下所示:
i 1 2 3 4 5 6 7
val[i] 2 3 13 1 5 21 8
ptr[i] 2 5 6 1 7 0 3
rank 2 3 6 1 4 7 5
head=4 有序表:1,2,3,5,8,13,21
采用shuffle()方法对val序列进行随机处理,保证最后通过ptr能按照从小到大顺序正确输出val序列的元素。
具体以
i 1 2 3 4 5
val 1 2 3 4 5
ptr 2 3 4 5 0
为例,如果i=1和i=2的列交换,则
i 1 2 3 4 5
val 2 1 3 4 5
ptr 3 1 4 5 0
继续交换,如果i=2和i=3的列交换,则
i 1 2 3 4 5
val 2 3 1 4 5
ptr 2 4 1 5 0
注意到这两种交换即为shuffle()随机处理过程中典型的两类列交换,分别是"序列两端任一端和序列中间元素交换"与"序列中间任两列元素交换"。以第一种交换为例,val交换的元素为第1和第2列,所以在ptr中找值为1和2的,并将值为2的重新赋值为1,值为1的重新赋值为2,如果没找到值为1或2的则不作处理。算法采用vector实现ptr,利用algorithm中的find()方法找出ptr中指定元素的下标位置并重新赋值,从而实现通过ptr即可按序输出val。find()元素也能找出val中第一个元素的位置,即为ptr中值为1的下标对应的val元素。
算法A为O(n)的确定算法,B为O(sqrt(n))的确定算法,算法D为概率算法。shuffle()耗时很多,对于顺序序列,算法B的表现和A一样差。随机算法D表现时好时坏。算法C表现始终很好。对于随机序列,算法B和算法C表现都很好,速度很快。而算法A效果要差。随机算法D表现时好时坏,算法具体运行的时间差别并不是很明显。
作业9根据搜索过的平均节点数确定最优的StepVegas,最终当n=8(八皇后)时结果比较合理,当n=12~20随着随机放置的马的数量增大,算法的成功率迅速降低为0,导致最后的结果很不合理。怀疑是由于当n增大时生成的随机数随机效果不好导致算法成功率迅速降低,没有被验证。
作业10由于求素数的算法为3/4正确、偏假的MC算法,导致当迭代次数为2~4时选出强伪素数的概率为(1-3/4)^(2~4),比较低的概率导致在100~10000中产生错误素数的比例很小。当改为迭代一次时,概率为1-3/4=1/4此时在100~10000中产生错误素数的比例稍微有所增加,也验证了MC算法迭代次数越多求出正确结果概率越大的结论。
其中作业5求集合大小的算法(求指正):
1 SetCount (X) { 2 k ← 0; S ← Ф; 3 a ← uniform(X); 4 do { 5 k++; 6 S ← S∪{a}; a ← uniform(X); 7 } while (a not in S) 8 return 2k2/π 9 }
其中作业7的shuffle()算法:
vector<int> Shuffle(int *val, vector<int> ptr, int n) { srand(time(0)); int i = 1, j = 1, k = 1, st = (int)sqrt(n*1.0); vector<int>::iterator ir,jr; for(; i < st; i++) { j = (rand()%(n-1) + 1); Swap(val, i, j); ptr = SwapVector(ptr, i, j); ir = find(ptr.begin(),ptr.end(),i); jr = find(ptr.begin(),ptr.end(),j); if(ir != ptr.end()){ ir = ptr.erase(ir,ir+1);//清除ptr中为i的值 ptr.insert(ir,j);//增加j } if(jr != ptr.end()){ jr = ptr.erase(jr,jr+1); ptr.insert(jr,i); } } return ptr; }
作业9截图:
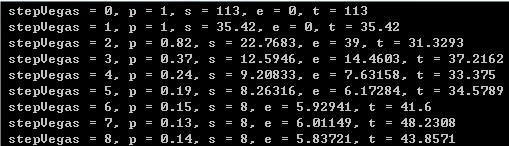
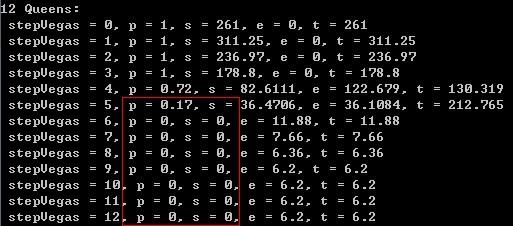
生成超出32767(2^15-1)的随机数方法:
1.rand()*rand()
2.rand()*1.0/RAND_MAX*n (n>32767)
3.对有m位数字的n,用随机生成每一位上的数字乘以对应的10的k次幂(k为该数字所在的位数,以321为例,3对应的k为2),最后相加
4.rand()<<16 + rand()
5.参考头文件里面的rand()函数,重写该函数
6.线性同余,x2 = ((x1 * 1103515245) + 12345) & 0x7fffffff,这个同余式可以[0, 2147483647]上随机。
其中1,3可能导致生成的随机数不是很随机。在windows下,RAND_MAX的值为32767(0x7fff),在linux下,RAND_MAX的值则是最大的32位正整数:2147483647(2的31次方减1:0xffffffff,该数也是欧拉发现的一个梅森素数)。其中6,线性同余参见http://www.cnblogs.com/xkfz007/archive/2012/03/27/2420154.html
对于5:
参见:http://www.oschina.net/code/explore/cygwin-1.7.7-1/newlib/libc/stdlib/rand_r.c
参见http://blog.csdn.net/ammana_babi/article/details/1437498
1 #include <stdlib.h> 2 3 /** Pseudo-random generator based on Minimal Standard by 4 Lewis, Goodman, and Miller in 1969. 5 6 I[j+1] = a*I[j] (mod m) 7 8 where a = 16807 9 m = 2147483647 10 11 Using Schrage's algorithm, a*I[j] (mod m) can be rewritten as: 12 13 a*(I[j] mod q) - r*{I[j]/q} if >= 0 14 a*(I[j] mod q) - r*{I[j]/q} + m otherwise 15 16 where: {} denotes integer division 17 q = {m/a} = 127773 18 r = m (mod a) = 2836 19 20 note that the seed value of 0 cannot be used in the calculation as 21 it results in 0 itself 22 */ 23 24 int 25 _DEFUN (rand_r, (seed), unsigned int *seed) 26 { 27 long k; 28 long s = (long)(*seed); 29 if (s == 0) 30 s = 0x12345987; 31 k = s / 127773; 32 s = 16807 * (s - k * 127773) - 2836 * k; 33 if (s < 0) 34 s += 2147483647; 35 (*seed) = (unsigned int)s; 36 return (int)(s & RAND_MAX); 37 }
1 static long my_do_rand(unsigned long *value) 2 { 3 /* 4 这个算法保证所产生的值不会超过(2^31 - 1)这里(2^31 - 1)就是 0x7FFFFFFF。 5 而 0x7FFFFFFF等于127773 * (7^5) + 2836,7^5 = 16807。 6 整个算法是通过:t = (7^5 * t) mod (2^31 - 1) 7 这个公式来计算随机值,并且把这次得到的值,作为下次计算的随机种子值。 8 */ 9 long quotient, remainder, t; 10 quotient = *value / 127773L; 11 remainder = *value % 127773L; 12 t = 16807L * remainder - 2836L * quotient; 13 if (t <= 0) 14 t += 0x7FFFFFFFL; 15 return ((*value = t) % ((unsigned long)RANDOM_MAX + 1)); 16 }
两者最后return处理方式不同但效果相同。
关于GSL(GNU Scientific Library)库的利用:
http://gnailuy.com/2011/07/10/gsl%E7%A7%91%E5%AD%A6%E8%AE%A1%E7%AE%97%E5%BA%93%E3%80%81%E9%9A%8F%E6%9C%BA%E5%8F%98%E9%87%8F%E7%9A%84erlang%E5%88%86%E5%B8%83%E4%B8%8Eweibull%E5%88%86%E5%B8%83/