本人博文《背包问题---01背包最优方案总数(原理剖析代码实现)》及
背包问题----完全背包(最优方案总数分析及实现)
中分别谈过“01背包”和“完全背包”实现最大价值的方案总数,这里我们再讨论一下这两种背包被物品刚好装满的方案总数。网上各大公司经常出题目:假设现在有1元、2元、5元的纸币很多张,现在需要20块钱,你能给多少种找钱方案,这就可以认为是完全背包问题,即背包容量为20,物品体积分别为1、2、5。
还有公司出题目:给定一个数m,将m拆成不同的自然数的和的形式有多少种方案,这就是典型的01背包问题,背包容量为m,物品件数为k,这里面的k是隐含条件,可以求出来,因为m最多由1+2+…+k得到,由此可以根据m求得物品件数的上限。
现在切入正题,我们先谈“01背包”将背包刚好装满的方案总数。“完全背包”和“01背包”极为相似,只有极少量代码变动。
01背包装满的问题抽象化:
设背包容量为V,一共N件物品,每件物品体积为C[i],每件物品的价值为W[i],求将背包装满的方案总数。
1) 子问题定义:F[i][j]表示前i件物品中选取若干件物品放入剩余空间为j的背包中刚好把背包装满的方案总数。
2) 根据第i件物品体积和所剩背包容量大小进行决策
 (1-1)
(1-1)
注意初始化条件为F[0][0]=1,即没有物品放入容量为0的背包刚好放满的方案数为1。
故可得伪代码如下:
- F[0][0] ← 1
- for i ← 1 to N
- do for j ← 0 to V
- if (j < C[i])
- then F[i][j] ← F[i-1][j]
- else
- F[i][j] ← F[i-1][j]+F[i-1][j-C[i]]
- return F[N][V]
上述代码的空间复杂度为O(NV),由状态方程可知,F[i][]只与F[i-1][]的状态有关,故可以用一维数组来代替二维数组,以降低空间复杂度为O(V)。
降低空间复杂度为O(V)的伪代码如下:
- F[0] ← 1
- for i ← 1 to N
- do for j ← V to C[i]
- if (j >= C[i])
- then F[j] ← F[j]+F[j-C[i]]
- return F[V]
注意对V的遍历变为逆序,至于为什么这样,请看本人博文《背包问题---01背包最优方案总数(原理剖析代码实现)》。
接下来看看“完全背包”到底有哪些变化。看过《背包九讲》或者本人博文《背包问题----完全背包(详解|代码实现|背包具体物品的求解)》的读者应该会能很快想到状态方程的变形,如下:
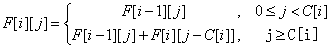 (1-2)
(1-2)
不错,状态方程是这样。F[i-1][j]表示背包中不含第i种物品时把背包装满的方案,F[i][j-C[i]]表示至少包含一件第i种物品把背包装满的方案总数。所以,当j<C[i]时F[i][j] = F[i-1][j];当j >= C[i]时, F[i][j] = F[i][j-C[i]] + F[i-1][j],为什么是两者的和,因为F[i][j-C[i]]和F[i-1][j]都是[i][j]状态时把背包装满的方案,且两者互斥。
伪代码如下:
- F[0][0] ← 1
- for i ← 1 to N
- do for j ← 0 to V
- if (j < C[i])
- then F[i][j] ← F[i-1][j]
- else
- F[i][j] ← F[i-1][j]+F[i][j-C[i]]
- return F[N][V]
同样上述伪代码的空间复杂度为O(NV),我们也可以通过用一维数组来降低空间复杂度为O(V)。
伪代码如下:
- F[0] ← 1
- for i ← 1 to N
- do for j ← C[i] to V
- if (j >= C[i])
- then F[j] ← F[j]+F[j-C[i]]
- return F[V]
注意:上面对V的遍历为正序,为什么?请参考本人博文《背包问题----完全背包(详解|代码实现|背包具体物品的求解)》。
下面提过两种这两种背包的实现代码
01背包装满的方案总数:
//时间复杂度O(NV)空间复杂度O(NV)
#include<iostream>
using namespace std;
#define Size 1111
//int dp[Size];
int MethodTable[Size][Size];
int Max(int x,int y)
{
return x>y?x:y;
}
int Package01_FullOfPackage(int Weight[], int nLen, int nCapacity)
{
MethodTable[1][0] = 1;//初始化
for(int i = 2; i <= nLen+1; i++)
{
for(int j = 0; j <= nCapacity; j++)
{
if(j < Weight[i-1])
MethodTable[i][j] = MethodTable[i-1][j];
else
MethodTable[i][j] = MethodTable[i-1][j] + MethodTable[i-1][j-Weight[i-1]];
}
}
cout << "MethodTable:" << endl;
// PrintTowDimArray(MethodTable,nLen+1,nCapacity+1);
return MethodTable[nLen+1][nCapacity];
}
int main()
{
//int Weight[] = {1,1,1,1,1,1};
int Weight[Size];
int nCapacity;//空间
int n_goods;//数量
cin>>n_goods>>nCapacity;
for(int k=1;k<=n_goods;k++)
cin>>Weight[k];
cout << "AllCount:" << Package01_FullOfPackage(Weight,n_goods,nCapacity) << endl;
// cout << "AllCount:" << Package01_FullOfPackage_Compress(Weight,sizeof(Weight)/sizeof(int),nCapacity) << endl;
return 0;
}
//时间复杂度O(NV)空间复杂度O(V)
#include<iostream>
using namespace std;
#define Size 1111
int MethodTable[Size];
int Max(int x,int y)
{
return x>y?x:y;
}
int Package01_FullOfPackage(int Weight[], int nLen, int nCapacity)
{
MethodTable[0]= 1;//初始化
for(int i = 1; i <= nLen; i++)
{
for(int j = nCapacity; j >=Weight[i];j--)
{
if(j >= Weight[i])
MethodTable[j] += MethodTable[j-Weight[i]];
}
}
cout << "MethodTable:" << endl;
// PrintTowDimArray(MethodTable,nLen+1,nCapacity+1);
return MethodTable[nCapacity];
}
int main()
{
//int Weight[] = {1,1,1,1,1,1};
int Weight[Size];
int nCapacity;//空间
int n_goods;//数量
cin>>n_goods>>nCapacity;
for(int k=1;k<=n_goods;k++)
cin>>Weight[k];
cout << "AllCount:" << Package01_FullOfPackage(Weight,n_goods,nCapacity) << endl;
// cout << "AllCount:" << Package01_FullOfPackage_Compress(Weight,sizeof(Weight)/sizeof(int),nCapacity) << endl;
return 0;
}
完全背包装满的方案总数:
//时间复杂度O(NV)空间复杂度O(NV)
- int Package02_FullOfPackage(int Weight[], int nLen, int nCapacity)
- {
- int** MethodTable = NULL;
- CreateTwoDimArray(MethodTable,nLen+1,nCapacity+1);
- MethodTable[0][0] = 1;
- for(int i = 1; i <= nLen; i++)
- {
- for(int j = 0; j <= nCapacity; j++)
- {
- if(j < Weight[i-1])
- MethodTable[i][j] = MethodTable[i-1][j];
- else
- MethodTable[i][j] = MethodTable[i-1][j]+MethodTable[i][j-Weight[i-1]];
- }
- }
- cout << "MethodTable:" << endl;
- PrintTowDimArray(MethodTable,nLen+1,nCapacity+1);
- int nRet = MethodTable[nLen][nCapacity];
- DestroyTwoDimArray(MethodTable,nLen+1);
- return nRet;
- }
//时间复杂度O(NV)空间复杂度O(V)
- int Package02_FullOfPackage_Compress(int Weight[], int nLen, int nCapacity)
- {
- int * MethodTable = new int [nCapacity+1];
- memset(MethodTable,0,(nCapacity+1)*sizeof(int));
- //initiallize all MethodTable[0] with 1
- MethodTable[0] = 1;
- for(int i = 0; i < nLen; i++)
- {
- for(int j = Weight[i]; j <= nCapacity; j++)
- {
- if(j >= Weight[i])
- MethodTable[j] += MethodTable[j-Weight[i]];
- }
- }
- int nRet = MethodTable[nCapacity];
- delete [] MethodTable;
- return nRet;
- }
//测试代码
- int main()
- {
- int Weight[] = {1,2,5};
- //int Weight[] = {2,2,2};
- int nCapacity = 20;
- cout << "AllCount:" << Package02_FullOfPackage(Weight,sizeof(Weight)/sizeof(int),nCapacity) << endl;
- cout << "AllCount:" << Package02_FullOfPackage_Compress(Weight,sizeof(Weight)/sizeof(int),nCapacity) << endl;
- return 0;
- }
版权声明:本文为博主原创文章,未经博主允许不得转载。