对于一棵树,求两个节点的最近公共祖先(LCA)。
如下图:(以下数字代表对应编号的节点)
11 和 66 的 LCA 是 88 。
1111 和 11 的 LCA 是 88 。
1111 和 1515 的 LCA 是 44 。
1414 和 1313 的 LCA 是 11 。
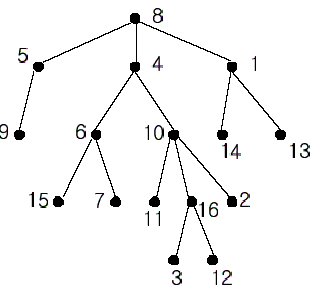
以洛谷P3379模板题为例
方法一:用倍增来在线求 LCA ,时间和空间复杂度分别是 O((n+q)logn)O((n+q)logn) 和 O(nlogn)O(nlogn) 。
对于这个算法,我们从最暴力的算法开始:
①如果 aa 和 bb 深度不同,先把深度调浅,使他变得和浅的那个一样
②现在已经保证了 aa 和 bb 的深度一样,所以我们只要把两个一起一步一步往上移动,直到他们到达同一个节点,也就是他们的最近公共祖先了。
#include<iostream> #include<cstring> #include<algorithm> #include<vector> using namespace std; const int maxn=5e5+5; int lg[maxn];//log 2n向下取整 const int maxbit=20; vector<int>G[maxn]; int depth[maxn];//记录每个节点的深度 int father[maxn][maxbit];//father[i][j]指的是i节点往上2^j的节点 void dfs(int nowp,int fa) { depth[nowp]=depth[fa]+1;//当前节点深度是父节点深度+1 father[nowp][0]=fa; for(int j=1;j<=lg[depth[nowp]];j++)//倍增求father father[nowp][j]=father[father[nowp][j-1]][j-1]; for(int i=0;i<G[nowp].size();i++) { if(G[nowp][i]!=fa) dfs(G[nowp][i],nowp); } } int LCA(int u,int v) { if(depth[u]<depth[v])//维护u的深度最大 swap(u,v); while(depth[u]!=depth[v]) u=father[u][lg[depth[u]-depth[v]]];//使两个节点在同一高度; if(u==v) return u; for(int j=lg[depth[u]];j>=0;--j) { if(father[u][j]!=father[v][j]) { u=father[u][j]; v=father[v][j]; } } //得到最近公共祖先下一位; return father[u][0]; } int main() { lg[0]=-1; for(int i=1;i<maxn;i++) lg[i]=lg[i>>1]+1; int n,m,s;int x,y; scanf("%d%d%d",&n,&m,&s); for(int i=1;i<n;i++) { scanf("%d%d",&x,&y); G[x].push_back(y); G[y].push_back(x); } dfs(s,0);//假设根结点的父节点为0; while(m--) { scanf("%d%d",&x,&y); printf("%d ",LCA(x,y)); } return 0; }
方法二:
现在来介绍一种 O(nlogn)O(nlogn) 预处理,O(1)O(1) 在线查询的算法。
RMQ 的意思大概是“区间最值查询”。顾名思义,用 RMQ 来求 LCA 是通过 RMQ 来实现的。
首先,您可以了解一下 dfs 序。链接:http://www.cnblogs.com/zhouzhendong/p/7264132.html
在 dfs 的过程中,退出一个子树之后就不会再进入了。这是个很好的性质。
所以很显然,一个子树中深度最浅的节点必定是该子树的树根。
显然,两个节点的 LCA 不仅是两个节点的最近公共祖先,而且是囊括这两个节点的最小子树的根,即囊括这两个节点的最小子树中的深度最小的节点。
我们来想一想如何得到这个节点。
现在,我们稍微修改一下 dfs 序,搞一个欧拉序。
欧拉序,就是每次从 father(x)father(x) 进入节点 xx 或者从子节点回溯到 xx 都要把 xx 这个编号扔到一个数组的最后。
这样最终会得到一个长度约为 2n2n 的数列。(考虑每一个节点贡献为 22 ,分别是从其父亲进入该节点,和从该节点回到其父亲)

例如,上图这棵树的一个欧拉序为 8,5,9,5,8,4,6,15,6,7,6,4,10,11,10,16,3,16,12,16,10,2,10,4,8,1,14,1,13,1,88,5,9,5,8,4,6,15,6,7,6,4,10,11,10,16,3,16,12,16,10,2,10,4,8,1,14,1,13,1,8 。
建议跟着我给出的欧拉序走一遍,再次理解欧拉序的含义。
再注意到,一对点的 LCA 不仅是囊括这两个节点的最小子树中的深度最小的节点,还是连接这对点的简单路径上深度最小的点。
而且从离开 aa 到进入 bb 的这段欧拉序必然包括所有这对点之间的简单路径上的所有点,所以我们考虑求得这段欧拉序中所包含的节点中的 深度最小的点即其 LCA 。
从 aa 到 bb 的这段欧拉序会包含这棵子树中的其他节点,但是不会影响这个最浅点的求得,因为“一对点的 LCA 是囊括这两个节点的最小子树中的深度最小的节点”。
显然, aa 到 bb 这段欧拉序是个连续区间。
你可以用线段树维护,但是线段树太 low 了。
现在我们考虑通过预处理来 O(1)O(1) 获得这个最浅点。
于是我们要学习一个叫做 ST表 的东西来搞定这个。(和之前倍增中处理的 fafa 数组差不多)
我再放一篇大佬博客来介绍 RMQ 与 ST表 : https://blog.csdn.net/qq_31759205/article/details/75008659
代码:
#include<iostream> #include<algorithm> #include<vector> #include<cstring> using namespace std; const int maxn=5e5+5; const int maxbit=20; vector<int>G[maxn]; int order[maxn*2];//dfs序 int depth[maxn*2];//dfs序对应点深度 int st[maxn*2][maxbit];//st[i][j]指的是dfs序包含i在内的2^j个点深度最小的点的编号 int first_place[maxn];//储存dfs序每一个结点最早出现的位置 int lg[maxn*2]; inline int read()//读入优化 { char ch=getchar(); int x=0,f=1; while((ch>'9'||ch<'0')&&ch!='-') ch=getchar(); if(ch=='-') { f=-1;ch=getchar(); } while('0'<=ch&&ch<='9') { x=x*10+ch-'0'; ch=getchar(); } return x*f; } int cnt=0;//dfs序长度 void dfs(int nowp,int dep)//nowp当前点,dep父节点深度 { ++cnt; first_place[nowp]=cnt;//每个点进一次dfs,所以有这个 order[cnt]=nowp;//dfs第几个存nowp节点 depth[cnt]=dep+1; for(int i=0;i<G[nowp].size();i++) { int to=G[nowp][i]; if(first_place[to]==0)//不是父节点 { dfs(to,dep+1); ++cnt; order[cnt]=nowp; depth[cnt]=dep+1; } } } void st_init()//求st表 0(nlog(n)) { for(int i=1;i<=cnt;i++) st[i][0]=i; int a,b; for(int j=1;j<=lg[cnt];j++) { for(int i=1;i+(1<<j)-1<=cnt;i++) { a=st[i][j-1]; b=st[i+(1<<(j-1))][j-1]; if(depth[a]<depth[b]) st[i][j]=a; else st[i][j]=b; } } } int main() { lg[0]=-1; for(int i=1;i<maxn*2;i++) lg[i]=lg[i>>1]+1; int n,m,s; n=read(); m=read(); s=read(); int x,y; for(int i=1;i<n;i++) { x=read(); y=read(); G[x].push_back(y); G[y].push_back(x); } dfs(s,0); st_init(); while(m--) { x=read(); y=read(); x=first_place[x]; y=first_place[y]; if(x>y) swap(x,y); int k=lg[y-x]; int a,b; a=st[x][k]; b=st[y-(1<<k)+1][k]; if(depth[a]<depth[b]) printf("%d ",order[a]); else printf("%d ",order[b]); } return 0; }
方法三:
LCA_Tarjan
TarjanTarjan 算法求 LCA 的时间复杂度为 O(n+q)O(n+q) ,是一种离线算法,要用到并查集。(注:这里的复杂度其实应该不是 O(n+q)O(n+q) ,还需要考虑并查集操作的复杂度 ,但是由于在多数情况下,路径压缩并查集的单次操作复杂度可以看做 O(1)O(1),所以写成了 O(n+q)O(n+q) 。)
TarjanTarjan 算法基于 dfs ,在 dfs 的过程中,对于每个节点位置的询问做出相应的回答。
dfs 的过程中,当一棵子树被搜索完成之后,就把他和他的父亲合并成同一集合;在搜索当前子树节点的询问时,如果该询问的另一个节点已经被访问过,那么该编号的询问是被标记了的,于是直接输出当前状态下,另一个节点所在的并查集的祖先;如果另一个节点还没有被访问过,那么就做下标记,继续 dfs 。
当然,暂时还没那么容易弄懂,所以建议结合下面的例子和标算来看看。

(下面的集合合并都用并查集实现)
比如:8−1−14−138−1−14−13 ,此时已经完成了对子树 11 的子树 1414 的 dfsdfs 与合并( 1414 子树的集合与 11 所代表的集合合并),如果存在询问 (13,14)(13,14) ,则其 LCA 即 getfather(14)getfather(14) ,即 11 ;如果还存在由节点 1313 与 已经完成搜索的子树中的 节点的询问,那么处理完。然后合并子树 1313 的集合与其父亲 11 当前的集合,回溯到子树 11 ,并深搜完所有 11 的其他未被搜索过的儿子,并完成子树 11 中所有节点的合并,再往上回溯,对节点 11 进行类似的操作即可。
#include<iostream> #include<vector> #include<cstring> using namespace std; const int maxn=5e5+5; struct node { int x,y,lca; }query[maxn]; int fa[maxn]; int vis[maxn]; vector<int>G[maxn]; vector<int>Q[maxn]; int find(int x) { if(fa[x]==x) return x; else return fa[x]=find(fa[x]); } void dfs(int u) { vis[u]=1; for(int i=0;i<Q[u].size();i++) { int qid=Q[u][i]; if(query[qid].x==u) { if(vis[query[qid].y]) { query[qid].lca=find(query[qid].y); } } else { if(vis[query[qid].x]) query[qid].lca=find(query[qid].x); } } for(int i=0;i<G[u].size();i++) { int v=G[u][i]; if(vis[v]) continue; else { dfs(v); fa[v]=u; } } } int main() { int n,m,s; for(int i=1;i<maxn;i++) fa[i]=i; scanf("%d%d%d",&n,&m,&s); int x,y;n--; while(n--) { scanf("%d%d",&x,&y); G[x].push_back(y); G[y].push_back(x); } for(int i=1;i<=m;i++) { scanf("%d%d",&query[i].x,&query[i].y); Q[query[i].x].push_back(i); Q[query[i].y].push_back(i); } dfs(s); for(int i=1;i<=m;i++) { printf("%d ",query[i].lca); } return 0; }