支持向量机,作为新手,给出新手的学习心得,可能能让新手更容易理解吧。
对于SVM的讲解,网上已经很多了,支持向量机通俗导论(理解SVM的三层境界) 这一篇blog写得很好,不过对于一个新手来说,我感觉行文逻辑还是有点怪,作者的写法是遇到问题解决问题,无可厚非这是一个很好的学习习惯,不过真正让学习的人看起来却没有一个提纲挈领的作用,而这次学习遇到这个算法,写下自己的学习笔记,里面也写了一点自己学习的思路,只是代表自己的一点愚见,本文主要参考上述blog以及该blog列出的参考文献。python算法实现,仍然是机器学习实战这本书。
SVM怎么用
学习这个东西就是为了用这个东西,目前网上有很多开源,免费的软件可以使用。对于基本的使用会增加对这个算法的了解。
为了能让大家先有一个感性的认识,通过 libsvm软件给出这么一个过程。
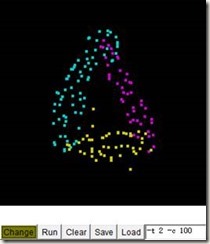
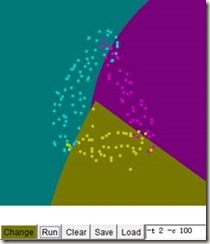
在http://www.csie.ntu.edu.tw/~cjlin/libsvm/网站上有一个Java Applet的小应用,自己加一些数据,自动分类,具体效果图如下:
如何正确使用,那就要学习其算法,了解其过程;
如何精确使用,那就要了解其原理;
SVM求解过程(算法)
很多人把SVM的引入是通过逻辑回归,是一个很好的引导,算我愚笨,我没有发现逻辑回归转化到SVM有多么自然,可能是数学理论上这样的承接比较自然,但是对于新手我来说,感觉还是有点吃力。回到主题。
算法,是一个给出输入得到输出的这么一个过程。先说一下这个问题,然后我们给出输入以及我们想得到的输出。
问题:有N个n维的样本点: x1,x2,x3,...,xN∈R。 对于给定的i,xi对应一个yi∈{−1,1},我们给出一个任意x,判定其属于哪一个y。
输出:一个分类器,就是我再给出一个x,通过该分类器,可以得出该x属于哪个分类。即y等于+1还是-1。
至于这边为什么用1与-1作为分类不用1或者0,我认为是为了方便计算,下面从给出的最优化问题就可以看出。我们先看线性分类,
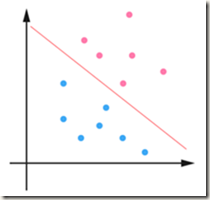
对于分类给出如下图:
这是二维的一个平面,红色的线可以作为分类线将红色的点与蓝色的点分开。
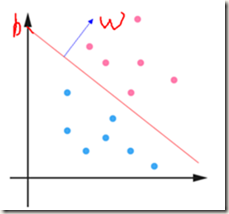
在超平面中,对于中间这条红色的分界,可以通过![]() 表示,根据几何的关系我们知道
表示,根据几何的关系我们知道![]() 是红色分界线的法向量,
是红色分界线的法向量,![]() 是截距,我们可以知道这个直线就是由w和b控制的,即我们知道了w和b就知道了这条直线(超平面想象不出来,可以从二维平面考虑,即为
是截距,我们可以知道这个直线就是由w和b控制的,即我们知道了w和b就知道了这条直线(超平面想象不出来,可以从二维平面考虑,即为![]() ),如下图。
),如下图。
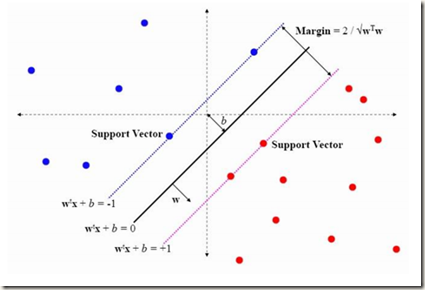
下面给出一个新的名词,最大间隔,这也就是SVM变成优化问题的目标函数,从下图我们了解一下最大间隔、支持向量
至于为什么这边是![]() 或者
或者![]() 呢,主要考虑也是计算方便。如果我们设为
呢,主要考虑也是计算方便。如果我们设为![]() 或者
或者![]() ,两边同时除以2就可以了。再重新设定一下
,两边同时除以2就可以了。再重新设定一下![]() 就可以了。
就可以了。
两条直线直接的距离,根据高中的知识,我们假设是二维的,有:
所以我们要求这个距离最大,也就是求![]() 最小值,为了方便计算转化为
最小值,为了方便计算转化为![]() 最小值。另外我们有这么一个条件,即从上面的图就可以看出
最小值。另外我们有这么一个条件,即从上面的图就可以看出
这就是为什么前面使用1和-1作为分类标准,便于化简计算。这样我们就可以把SVM转化为如下优化问题。
这是求具体条件的极值,如果条件是等式,我们采用拉格朗日乘数法(高等数学下册),但是这边的条件是不等式,我们通过KKT条件去求解,转化如下:
如何求解
这个 支持向量机通俗导论(理解SVM的三层境界)的第二层境界讲述比较全面,下面主要参考该文。
主要过程,转化求对偶问题,首先固定![]() ,要让 L 关于 w 和 b 最小化,我们分别对w,b求偏导数:
,要让 L 关于 w 和 b 最小化,我们分别对w,b求偏导数:
以上结果代回上述的 L
最后得到:
这样x,y是已知的,就只有![]() ,下面对其求解。求解算法用SMO,这个在书中会实现。
,下面对其求解。求解算法用SMO,这个在书中会实现。
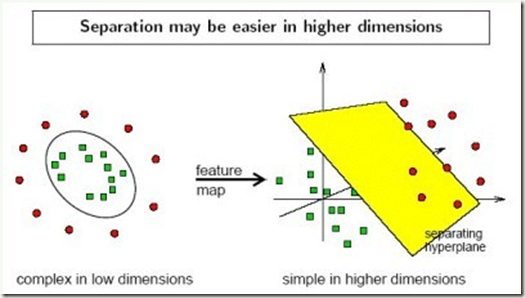
低维空间线性不可分,转高维空间
上述是线性可分,就是如上图,但是如果是线性不可分,这样我们就需要核函数。下图比较经典。
其核心思想是将低维转换到高维,利用转换后高维空间数据的稀疏性,可能可以线性可分。
具体怎么转换我们先不考虑,我们要考虑的是,我们转换到高维空间之后,主要还是求距离跟角度这些量。下面我们先给出变换
下面我们来求解高维空间中的距离与角度。
我们会发现高维空间中的距离跟角度我们都可以转化为内积进行计算。
这样如果我们的核函数就是内积的变换,那这样我们就可以在不用知道低维空间如何转换成高维空间的。
也就是我们定义核函数![]() ,这样我们上面的距离跟角度的计算直接转化为核函数,那我们的核函数到底是什么呢
,这样我们上面的距离跟角度的计算直接转化为核函数,那我们的核函数到底是什么呢
我们的内核函数一般为如下形式:
线性核
多项式核
高斯核
线性核很容易理解,就相当于没有变换。其他内核函数在使用的时候注意。
只要理解我们只要知道了内核函数,这样我们就可以把高维空间中的距离角度等值的计算又转化到低维空间上进行计算。
则:
那我们上述在高维空间中的计算也就是最后的![]() 转换成内核函数的计算就可以了。
转换成内核函数的计算就可以了。
高维空间也不完全线性可分
下面由于我们的数据是有噪声的,不可能完全线性可分,这样我们就要引入松弛变量
我们,原来的约束条件为:

现在考虑到噪声问题,约束条件变成了:

其中 称为松弛变量
称为松弛变量
如果 任意大的话,那任意的超平面都是符合条件的了,我们希望
任意大的话,那任意的超平面都是符合条件的了,我们希望 尽可能的小。我们考虑所有的
尽可能的小。我们考虑所有的 ,得到如下:
,得到如下:

我们再加上C来对我们这个容忍值 进行控制。
进行控制。
下面我们写出完整的目标函数式:

用之前的方法将限制或约束条件加入到目标函数中,得到新的拉格朗日函数,如下所示:

分析方法和前面一样,转换为另一个问题之后,我们先让 针对
针对 、
、 和
和 最小化:
最小化:

将  带回
带回  并化简,得到和原来一样的目标函数:
并化简,得到和原来一样的目标函数:

不过,由于我们得到 而又有
而又有 (作为 Lagrange multiplier 的条件),因此有
(作为 Lagrange multiplier 的条件),因此有 ,所以整个 dual 问题现在写作:
,所以整个 dual 问题现在写作:

一样,这边转化为高维空间之后也就是上式得内积转化为内核函数计算。
这样基本的SVM就可以了解了。
实战的东西比较多,放到最后在解决。

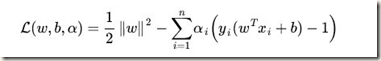
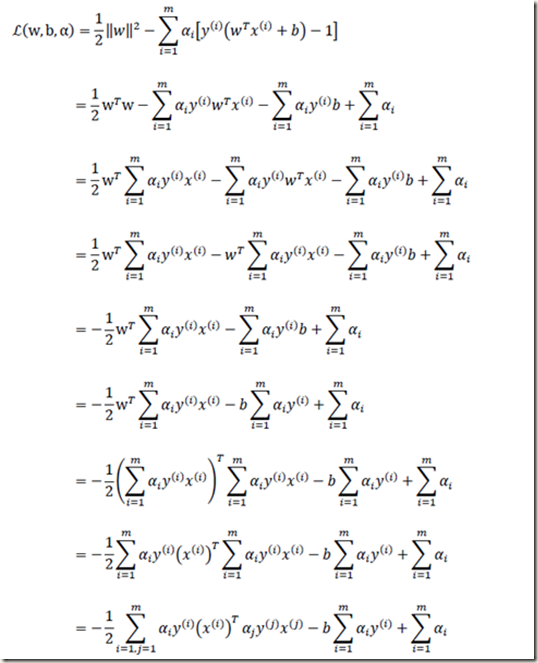
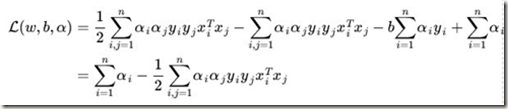
![clip_image002[26] clip_image002[26]](https://images0.cnblogs.com/blog/311205/201401/151318052671.png)
![clip_image002[28] clip_image002[28]](https://images0.cnblogs.com/blog/311205/201401/151318062987.png)
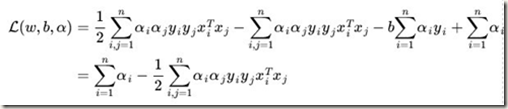
![clip_image002[33] clip_image002[33]](https://images0.cnblogs.com/blog/311205/201401/151318099087.png)