第六章 近似算法
一. 近似算法的基本概念

首先什么是NP-完全问题(这部分参考博文:http://blog.csdn.net/xueyong4712816/article/details/6509592):NP=Non-deterministic Polynomial,也就是多项式复杂程度的非确定性问题。要了解NP问题,先从P问题开始,P就是Polynomial(多项式)的意思。P类问题就是所有复杂度为多项式时间的问题的集合。多项式就是n^k+n^(k-1)+……等等其中k为任意整数(一般不会很大)。这个数看起来很大,其实人类计算机相对都能接受。就怕遇到指数方增长的问题。
接下来探讨非确定性问题。什么是非确定性问题呢?有些计算问题是确定性的,比如加减乘除之类,你只要按照公式推导,按部就班一步步来,就可以得到结果。但是,有些问题是无法按部就班直接地计算出来。比如,找大质数的问题。有没有一个公式,你一套公式,就可以一步步推算出来,下一个质数应该是多少呢?这样的公式是没有的。再比如,大的合数分解质因数的问题,有没有一个公式,把合数代进去,就直接可以算出,它的因子各自是多少?也没有这样的公式。这种问题的答案,是无法直接计算得到的,只能通过间接的“猜算”来得到结果。这也就是非确定性问题。而这些问题通常有个算法,它不能直接告诉你答案是什么,但可以告诉你,某个可能的结果是正确的答案还是错误的。这个可以告诉你“猜算”的答案正确与否的算法,假如可以在多项式时间内算出来,就叫做多项式非确定性问题。而如果这个问题的所有可能答案,都是可以在多项式时间内进行正确与否的验算的话,就叫完全多项式非确定问题。
完全多项式非确定性问题可以用穷举法得到答案,一个个检验下去,最终便能得到结果。但是这样算法的复杂程度,是指数关系,因此计算的时间随问题的复杂程度成指数的增长,很快便变得不可计算了。
了解了上述的概念之后,我们便可以理解ppt中的第二点:求解NP-完全问题很难,若输入规模小倒是可以穷举,否则用多项式算法近似,这也是本章的主题。


怎么理解那个Ratio Bound呢?第一点明白OPT是最优解,我们的近似解不可能优于它,所以对于最大化问题,A一定比OPT小而对于最小化问题A一定比OPT大,所以上面的连个max取了不同的值。注意这里的Ratio Bound指的是那个B(n),即是max{A/OPT, OPT/A}的上界。


结论:只要求出了Ratio Bound,就求出了相对误差。
二. 一些经典问题
1. 顶点覆盖问题

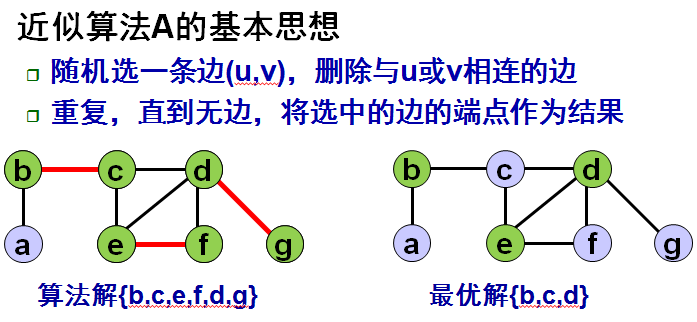
问题:给定一个N个点M条边的无向图G(点的编号从1至N),问是否存在一个不超过K个点的集合S,使得G中的每条边都至少有一个点在集合S中。简而言之就是在一无向图中找一个点集,满足:最小点集&&图中的每条边至少有一个点在这个点集中。这里一开始疑惑为什么顶点覆盖问题是NP-完全问题。。。 ,百度了下之后发现。。。。我了个擦。。。 Np问题这么难,等我把我那本算法导论NP完全性啃完再来分析下这里,现在的重点在近似算法上。
