第四章 贪心算法


这里需要注意的便是如何证明贪心算法得到的是最优解。

下面来一些例子:
1. 活动选择问题


现在感觉贪心算法真的是目前遇到过实现起来最简单的一个,但是问题在于用贪心算法得到的解是不是最优解呢?下面来证明:
第一步要证明问题具有最优子结构性质:

还是利用了这种先假设,再反证这种策略。对于最优解,如果这个解中所对应于子问题的子解不是子问题的最优解的话,那么对于在这个子问题的最优解,它和我们除掉的其余子问题的子解合并回到整个问题的解时一定会优于我们一开始假设的最优解,矛盾。故的出最优解的子解一定是子问题的最优解,即最优子结构性质。
第二步证明贪心选择性:

(1) 假定首选元素不是贪心选择所要的元素,证明将首元素替换成贪心选择所需元素,依然得到最优解;
(2) 数学归纳法证明每一步均可通过贪心选择得到最优解
这个思路很简单,如果最优解第一步不选f1,因为这个活动结束时间最早,所以它一定可以替换最优解中的第一个活动,并且S的最大相容集合并未减少,即将首元素替换成贪心选择所需元素,依然得到了最优解,故得证贪心选择性。
2. 哈弗曼编码

哈哈,考研数据结构有提到这个,就是要构造一棵带权路径长度最小的二叉树,这个很简单,就是每一步从所有节点中选择权值最小的两个节点合并成新的节点放入到原来的节点集合中,这个新的节点的权值等于原来两个节点的权值之和。之所以说是贪心算法是因为每一步都在当前节点集合中选当前权值最小的两个。

这里要注意的还是证明:


“因为z是C‘中的字符,所以它必为T” 中的叶子节点”,这句话该怎么理解呢?z是C’中的字符,按照哈夫曼树的构造规则,原先所有的节点构造后都在叶节点的位置上,所以z无论是在T’中还是T"中都作为叶节点存在(当然在T中不是,因为在T中z是一个中间节点的存在,连接x和y)。。。。。不过说实在的,关于这块最优子结构的证明我还是有些疑惑,也说不上来问题在哪。。。。 日后分析分析,现在考试为重。
3. 并查集




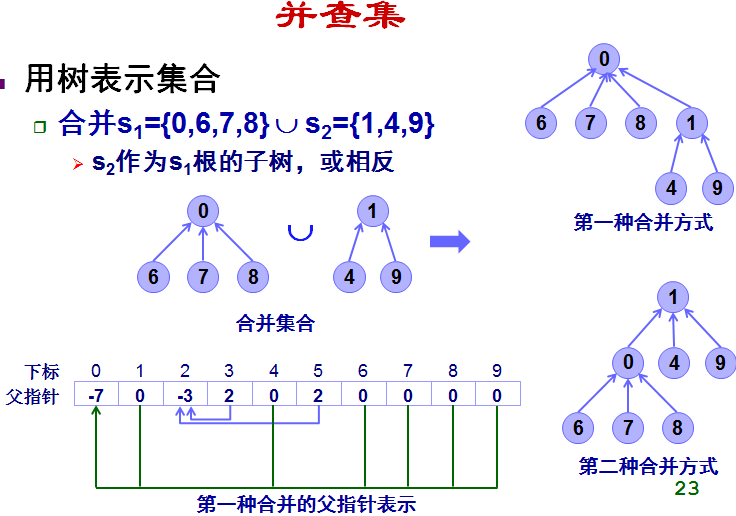

4. 最小生成树
考研数据结构里,这部分内容算是重点章节了吧。主要就是两个算法:克鲁斯卡尔(Kruskal)算法和普里姆(Prim)算法。克鲁斯卡尔(Kruskal)算法在图中每次选择权值最小的边,判断两端点是否属于不同集合,若是的话加入这条边将这两个端点连接成同一个集合。重复如此过程直至所有顶点在同一集合中。克鲁斯卡尔(Kruskal)算法经常需要判断权值最小的边的两端是否属于不同连通分量,所以可使用并查集技术加快判断速度。





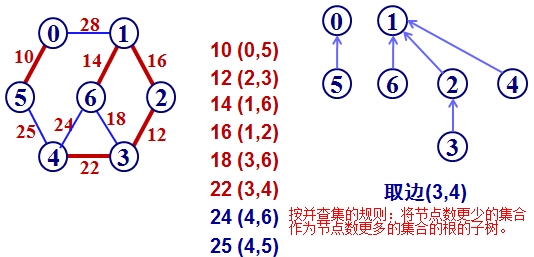


剩下的就是证明这块了:


这里的贪心选择性证明和前几题思路貌似有点不同,利用的是"假设--反证--矛盾"的策略。
5. 最短路径
又是考研数据结构中的知识,记得主要有两个算法:Dijkstra算法和Floyd算法,当初为了理解这两个算法死了多少脑细胞。。。。。 泪。。。。。




获取最短路径的方法:按照p和d数组反向读即可。比如到节点4的最短距离,看数组元素d[4]和p[4], d[4]=60, 那么得源点0到节点4的最短距离是60,p[4]=2, p[2]=3, p[3]=0, 得最短路径是0-3-2-4
国际惯例,最后的证明:


6. 个人总结
关于贪心算法,在问题的分析以及算法的实现上,个人觉得比动态和分治要简单。重要的是确定问题能用贪心算法得到最优解,即本章节中反复证明的最优子结构和贪心选择性。只有满足了这两个要素才能用贪心算法去解决问题。