首先发现那个双端队列一定长这样:
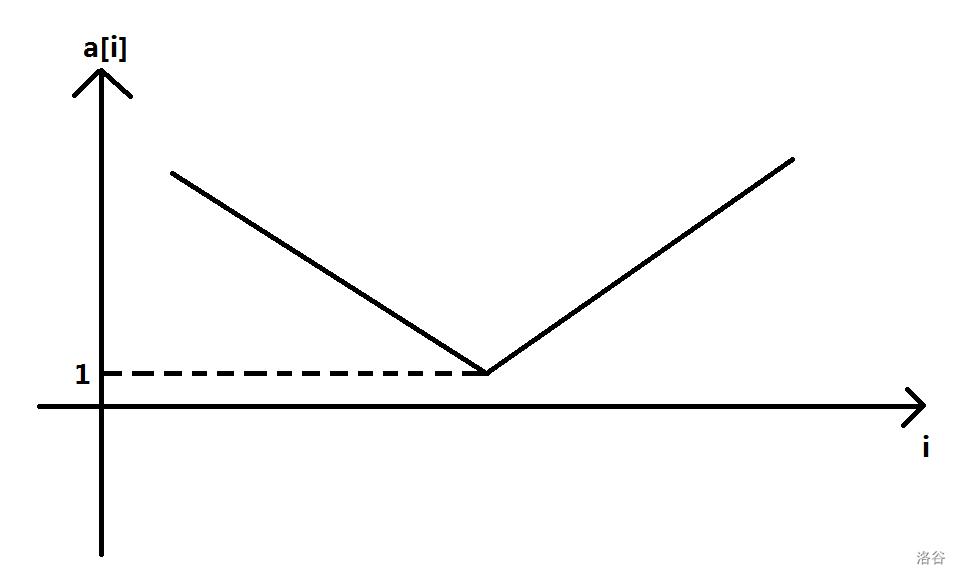
也就是说,这个队列中的数先单调递减,然后再单调递增,最小值为 1 1 1。
现在考虑从双端队列中取数,那么当我们取到 1 1 1 这个数时,我们会在原来的双端队列中取到类似这样的两个数列:(分别用红、蓝表示)
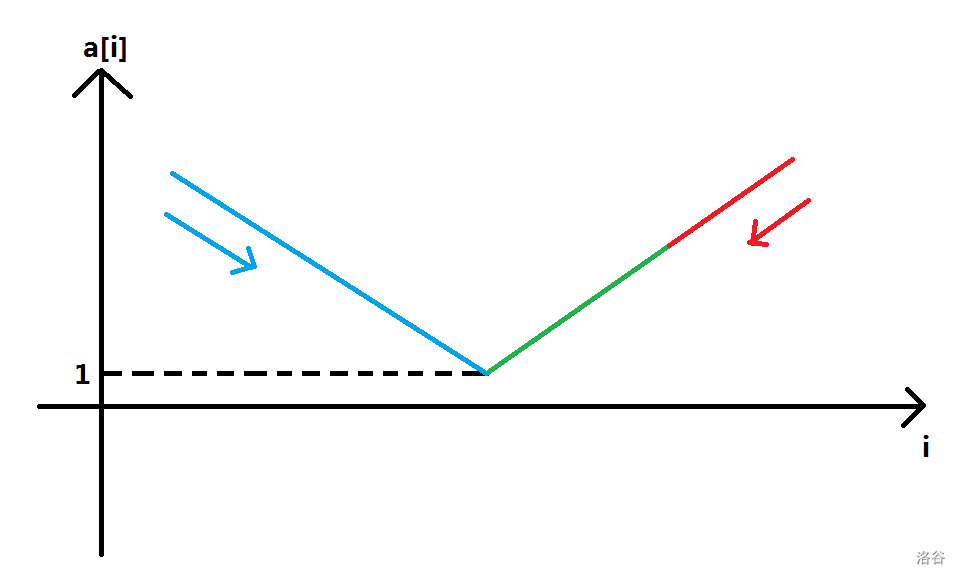
那么红、蓝两数列的总长度为 k k k,剩下的就是绿色的一段,长度为 n − k n-k n−k,我们每次可以从两端任意取,共取 n − k − 1 n-k-1 n−k−1 次,方案数为 2 n − k − 1 2^{n-k-1} 2n−k−1。
所以我们只用考虑前 k k k 个数的取法,然后乘上 2 n − k − 1 2^{n-k-1} 2n−k−1 就好了。
由图像,我们看一下弹出序列需要满足什么条件:
-
首先第 k k k 位肯定是 1 1 1。(题目要求)
-
前 k k k 个数,一定是由一个或两个单调递减的数列混合而成的(这两个数列就是图中的红、蓝两个数列),并且其中的一个单调递减的数列肯定包含 1 1 1 这个点(蓝色数列)。
-
后 n − k n-k n−k 个数,其最大值应小于某一个提到的单调数列的最小值。也就是绿色段的最大值小于红色段的最小值。
那我们不妨设 f ( i , j ) f(i,j) f(i,j) 表示已经取了前 i i i 个数,他们的最小值为 j j j 时的方案数。(满足上面的 3 3 3 个条件)
那么我们设选的这 i i i 个数分成的两个单调递减的序列分别为 A A A、 B B B,其中最小值 j j j 在 A A A 中, B B B 中的最小值为 m i n n minn minn。
设除了我们选的这 i i i 个数剩下的 n − i n-i n−i 个数组成的集合为 S S S, S S S 中最大的数为 m a x S maxS maxS。
大概可以用这张图表示:
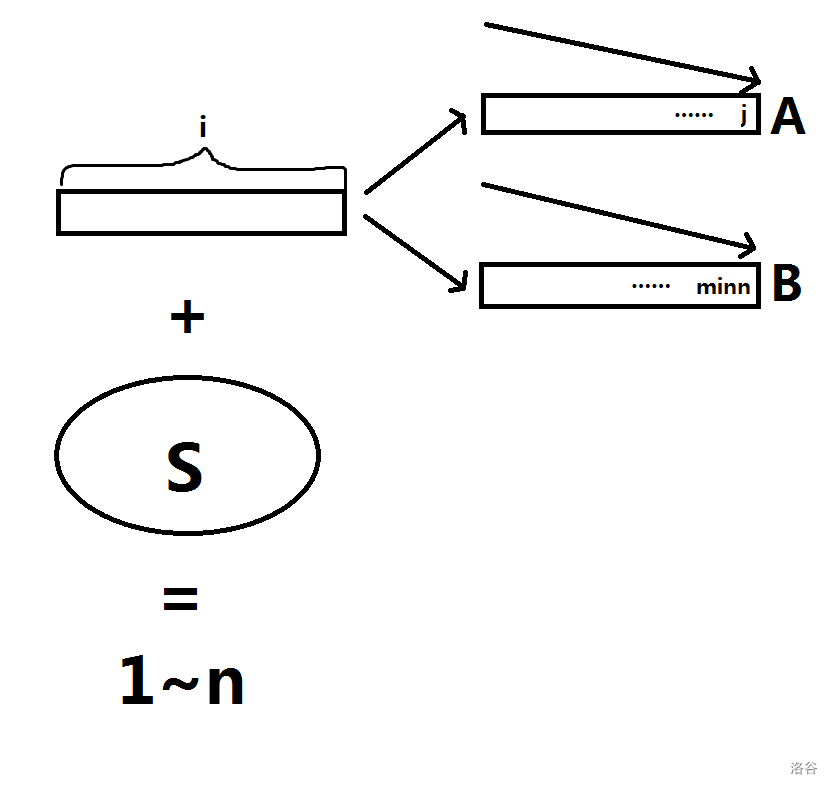
由 f ( i , j ) f(i,j) f(i,j) 的定义得, B B B 序列已经满足了第 3 3 3 个条件,即 m a x S < m i n n maxS<minn maxS<minn。
我们现在要从 S S S 中选一个数,加入 A A A 或 B B B 里面。
考虑构造:
-
假设加入的数 x x x 满足 x < j x<j x<j,那么我们就把它加到 A A A 的末尾,此时仍满足所有条件。所以 f ( i , j ) f(i,j) f(i,j) 向 f ( i + 1 , 1 ) ∼ f ( i + 1 , j − 1 ) f(i+1,1)sim f(i+1,j-1) f(i+1,1)∼f(i+1,j−1) 转移。
-
假设加入的数 x x x 满足 x ≥ j xgeq j x≥j,如果加入 A A A 中, A A A 就不满足单调递减的性质了,所以只能加入 B B B 中。
然后发现只能把 S S S 中的最大值 m a x S maxS maxS 加入到 B B B 的队尾(而且必须得满足 m a x S ≥ j maxSgeq j maxS≥j,不然会在第一种情况中算重)。
由于 m a x S maxS maxS 是 S S S 中的最大的数,所以当 m a x S maxS maxS 加入 B B B 数列成为 B B B 数列的最小值后,仍大于 S S S 中的所有数,满足条件。
所以 f ( i , j ) f(i,j) f(i,j) 向 f ( i + 1 , j ) f(i+1,j) f(i+1,j) 转移。
至于为什么 S S S 中除 m a x S maxS maxS 的某一个数 x x x 都不能加入 B B B 的队尾:因为加入后, B B B 中的最小值就变成了 x x x,而 S S S 中的最大值仍为 m a x S maxS maxS。此时 x < m a x S x<maxS x<maxS,不满足条件。
所以通过 f ( i , j ) f(i,j) f(i,j) 就可以向 f ( i + 1 , 1 ∼ j ) f(i+1,1sim j) f(i+1,1∼j) 转移了。
显然答案就是 2 n − k − 1 × ∑ i = 2 n − k + 2 f ( k − 1 , i ) 2^{n-k-1} imessumlimits_{i=2}^{n-k+2}f(k-1,i) 2n−k−1×i=2∑n−k+2f(k−1,i)。
还是有很多细节的,详见代码:
#include<bits/stdc++.h>
#define N 2010
#define ll long long
#define mod 1000000007
using namespace std;
int n,k;
ll f[N][N];
ll poww(ll a,ll b)
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=2;i<=n;i++) f[1][i]=1;
for(int i=1;i<k-1;i++)
{
f[i+1][n-i+1]=f[i][n-i+1];
for(int j=n-i;j>=2;j--)
f[i+1][j]=(f[i+1][j+1]+f[i][j])%mod;
}
ll ans=0;
for(int i=2;i<=n-k+2;i++)
ans=(ans+f[k-1][i])%mod;
if(k==1) ans=1;//特判1:k=1
if(n-k-1>=0) printf("%lld
",ans*poww(2,n-k-1)%mod);
else printf("%lld
",ans);//特判2:n=k
return 0;
}