一种非 DDP 的树剖做法。
主要是因为我不会 DDP,在考场上只想到了树剖。
首先如果没有修改,很容易想到朴素的 dp 做法:
设 v a l u val_u valu 表示 u u u 本身的权值, d p u dp_u dpu 表示以 u u u 为根的子树的答案,显然有:
d p u = min ( v a l u , ∑ v ∈ s o n ( u ) d p v ) dp_u=minleft(val_u,sum_{vin son(u)}dp_v ight) dpu=min⎝⎛valu,v∈son(u)∑dpv⎠⎞
就是要么割自己,要么割所有的子树。
为了方便表述,不妨设 s u m u = ∑ v ∈ s o n ( u ) d p v sum_u=sumlimits_{vin son(u)}dp_v sumu=v∈son(u)∑dpv。
但现在带修了怎么办呢?
DDP?不会!
首先肯定能发现如果修改了一个点 u u u 的权值加上了 t o to to( t o ≥ 0 togeq 0 to≥0),那么最多只有 u u u 到根的这条链上的点的 d p dp dp 值会改变。
考虑会做出那些改变:
首先 d p u dp_u dpu 的变化我们可以计算出来,不妨设 d p u dp_u dpu 的变化量为 x x x,那么对 s u m f a sum_{fa} sumfa 的贡献也是 x x x。( f a fa fa 为 u u u 的父亲)
那么如果 s u m f a + x ≤ v a l f a sum_{fa}+xleq val_{fa} sumfa+x≤valfa,那么 d p f a dp_{fa} dpfa 的变化量也是 x x x,那么对 f a fa fa 的父亲 g f a gfa gfa 的 s u m g f a sum_{gfa} sumgfa 的贡献也是 x x x。
定义一个函数 change ( u , x ) operatorname{change}(u,x) change(u,x) 表示当 s u m u sum_u sumu 需要增加 x x x 时,我们要进行的操作。
下面以 change ( f a , x ) operatorname{change}(fa,x) change(fa,x) 为例来详细阐述这个操作:
我们从 f a fa fa 开始往上找到第一个不满足 s u m v + x ≤ v a l v sum_v+xleq val_v sumv+x≤valv 的点 v v v,即满足 s u m v + x > v a l v sum_v+x> val_v sumv+x>valv,设 v v v 向 u u u 方向的儿子为 s o n son son, v v v 的父亲为 f f f。
图大概长这样:
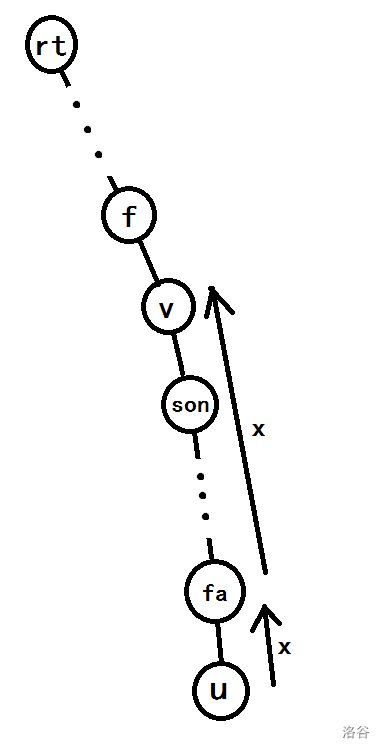
那么按照我们刚才的推论, u u u 到 s o n son son 的这一段点的 d p dp dp 值的变化量也都是 x x x。
但是当 s o n son son 向 s u m v sum_v sumv 贡献 x x x 的时候,发现 s u m v + x > v a l v sum_v+x>val_v sumv+x>valv。接下来分两种情况讨论:
-
若一开始 s u m v < v a l v sum_v<val_v sumv<valv,加上 x x x 后的新的 s u m v sum_v sumv 大于 v a l v val_v valv,那么 d p v dp_v dpv 就会变成 v a l v val_v valv,变化量就是 v a l v − s u m v val_v-sum_v valv−sumv(这里的 s u m v sum_v sumv 是没有加 x x x 之前的 s u m v sum_v sumv),对 f f f 的贡献也是 v a l v − s u m v val_v-sum_v valv−sumv。
那么到这里,我们又可以重复上述过程,进行操作 change ( f , v a l v − s u m v ) operatorname{change}(f,val_v-sum_v) change(f,valv−sumv)。
-
若一开始 s u m v ≤ v a l v sum_vleq val_v sumv≤valv,那么 s u m v sum_v sumv 加上 x x x 后对 d p v dp_v dpv 没有影响(因为 d p v dp_v dpv 还是 v a l v val_v valv),那么对 v v v 上面的祖先的 d p dp dp 值也不会产生影响。此时直接结束修改就好。
发现上述操作的实质其实就是将 r t rt rt 到 u u u 的链分为很多段,然后每一段的 d p dp dp 都是加上同一个权值。
那么现在的问题就变成每一段如何找到段顶 v v v,并且还要维护这一段修改 s u m sum sum 值。
后面那个很简单,用树剖维护就好,关键是如何找到 v v v。
找 v v v 和找 s o n son son 是等价的,观察一下 s o n son son 需要满足的要求: s o n son son 是最高的满足从 u u u 到 s o n son son 每一个的点 i i i 都满足 s u m i + x ≤ v a l i sum_i+xleq val_i sumi+x≤vali 的点。
移一下项,变成: x ≤ v a l i − s u m i xleq val_i-sum_i x≤vali−sumi。
这个时候就好办了,我们用树剖维护每一个点的 v a l − s u m val-sum val−sum,然后在线段树中维护每个区间的最小值:只有当一个区间的最小值大于等于 x x x 时,这个区间的所有值都大于等于 x x x。
那么就能按这种方法在线段树上找到 s o n son son,然后 v v v 就是 s o n son son 的父亲了。
发现我们还能同时在这棵线段树上通过修改 v a l − s u m val-sum val−sum 的值来修改 s u m sum sum 的值,很方便。
那么询问的时候答案就是 min ( v a l u , v a l u − query ( u ) ) min(val_u,val_u-operatorname{query}(u)) min(valu,valu−query(u))。(这里的 query ( u ) operatorname{query}(u) query(u) 其实就是在线段树中查询到的 v a l u − s u m u val_u-sum_u valu−sumu)
至于时间为什么能够保证:
首先一次修改的时间取决于分成的段数,因为每一段都是 O ( log n ) O(log n) O(logn) 的。
发现一次修改有可能就一段,有可能有 n n n 段,所以要从总体考虑这个事情。
考虑将分段的个数转化为每一个点 v v v 被分成段头的次数:
如果一个点 v v v 被分成段头,那么肯定是出现了 s u m v ≤ v a l v sum_vleq val_v sumv≤valv 但 s u m v + x > v a l v sum_v+x>val_v sumv+x>valv 的情况,那么加上 x x x 后的新的 s u m v sum_v sumv 会大于 v a l v val_v valv。又由于每一次修改操作都是给一个点的权值加上非负整数 x x x,所以对 s u m sum sum 的贡献也是非负整数。
所以除非修改自己的点权 v a l v val_v valv,在第一次 s u m v > v a l v sum_v>val_v sumv>valv 后, v v v 就不会被分为链头。又由于只有当 s u m v ≤ v a l v sum_vleq val_v sumv≤valv 且 s u m v + x > v a l v sum_v+x>val_v sumv+x>valv 的情况下 v v v 会被分为链头,所以每一个点最多只会被分为链头一次,所以段数不会大于 n n n 级别。
那么总时间复杂度就是 O ( ( n + m ) log 2 n ) O((n+m)log^2 n) O((n+m)log2n),可以通过。
代码如下,有很多细节:
#include<bits/stdc++.h>
#define N 200010
#define INF 0x7fffffffffffffff
#define ll long long
using namespace std;
int n,m;
int cnt,head[N],nxt[N<<1],to[N<<1];
int idx,fa[N],size[N],son[N],id[N],rk[N],top[N];
ll val[N],sumson[N],dp[N];
ll minn[N<<2],lazy[N<<2],mostl[N<<2];
void adde(int u,int v)
{
to[++cnt]=v;
nxt[cnt]=head[u];
head[u]=cnt;
}
void dfs(int u)
{
size[u]=1;
bool leaf=true;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(v==fa[u]) continue;
leaf=false;
fa[v]=u;
dfs(v);
sumson[u]+=dp[v];
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
if(leaf) sumson[u]=INF/100,dp[u]=val[u];
else dp[u]=min(val[u],sumson[u]);
}
void dfs1(int u,int tp)
{
top[u]=tp;
id[u]=++idx;
rk[idx]=u;
if(son[u]) dfs1(son[u],tp);
for(int i=head[u];i;i=nxt[i])
if(to[i]!=fa[u]&&to[i]!=son[u])
dfs1(to[i],to[i]);
}
void up(int k)
{
minn[k]=min(minn[k<<1],minn[k<<1|1]);
}
void downn(int k,ll v)
{
minn[k]-=v;
lazy[k]+=v;
}
void down(int k)
{
if(lazy[k])
{
downn(k<<1,lazy[k]);
downn(k<<1|1,lazy[k]);
lazy[k]=0;
}
}
void build(int k,int l,int r)
{
if(l==r)
{
minn[k]=val[rk[l]]-sumson[rk[l]];
mostl[k]=rk[l];
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
mostl[k]=mostl[k<<1];
up(k);
}
ll query(int k,int l,int r,int x)
{
if(l==r) return minn[k];
down(k);
int mid=(l+r)>>1;
if(x<=mid) return query(k<<1,l,mid,x);
return query(k<<1|1,mid+1,r,x);
}
void update(int k,int l,int r,int ql,int qr,ll v)
{
if(ql<=l&&r<=qr)
{
downn(k,v);
return;
}
down(k);
int mid=(l+r)>>1;
if(ql<=mid) update(k<<1,l,mid,ql,qr,v);
if(qr>mid) update(k<<1|1,mid+1,r,ql,qr,v);
up(k);
}
int find(int k,int l,int r,int ql,int qr,ll v)//找到son
{
if(ql<=l&&r<=qr&&minn[k]>=v) return mostl[k];
if(l==r) return -1;
down(k);
int mid=(l+r)>>1;
if(qr>mid)
{
int ans2=find(k<<1|1,mid+1,r,ql,qr,v);
if(ans2==mostl[k<<1|1]&&ql<=mid)
{
int ans1=find(k<<1,l,mid,ql,qr,v);
if(ans1==-1) return ans2;
return ans1;
}
return ans2;
}
return find(k<<1,l,mid,ql,qr,v);
}
void work(int u,ll v)
{
ll t=query(1,1,n,id[u]);
val[u]+=v,update(1,1,n,id[u],id[u],-v);
if(t>=0) return;
if(t+v>0) v=-t;
u=fa[u];
while(u)
{
int tmp=find(1,1,n,id[top[u]],id[u],v);//这里的tmp就是son
while(tmp==top[u])
{
update(1,1,n,id[tmp],id[u],v);
u=fa[tmp];
if(!u) return;
tmp=find(1,1,n,id[top[u]],id[u],v);
}
if(tmp==-1)
{
ll t=query(1,1,n,id[u]);
update(1,1,n,id[u],id[u],v);
if((v=t)<=0) return;
u=fa[u];
continue;
}
ll t=query(1,1,n,id[fa[tmp]]);
update(1,1,n,id[fa[tmp]],id[u],v);
if((v=t)<=0) return;
u=fa[fa[tmp]];
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&val[i]);
for(int i=1;i<n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
adde(u,v),adde(v,u);
}
dfs(1),dfs1(1,1);
build(1,1,n);
scanf("%d",&m);
int Q=0;
while(m--)
{
char opt[2];
scanf("%s",opt);
if(opt[0]=='Q')
{
Q++;
int u;
scanf("%d",&u);
printf("%lld
",min(val[u],val[u]-query(1,1,n,id[u])));
}
else
{
int u;ll v;
scanf("%d%lld",&u,&v);
work(u,v);
}
}
return 0;
}