最大流
部分资料来自:
目录
1.定义
2.基础表述
3.EK
4.Dinic
5.ISAP
6.HLPP
定义
从源点开始,经过所有路径最终到达汇点的所有流量和
流网络G=(V,E)是一个有向图,其中每条边(u,v)∈E均有一个非负容量c(u,v)>=0。如果(u,v)不属于E,则假定c(u,v)=0。流网络中有两个特别的顶点:源点s和汇点t。
下图展示了一个流网络的实例
其中每条边上的数对表示:实际有向边上的流量/最大容量
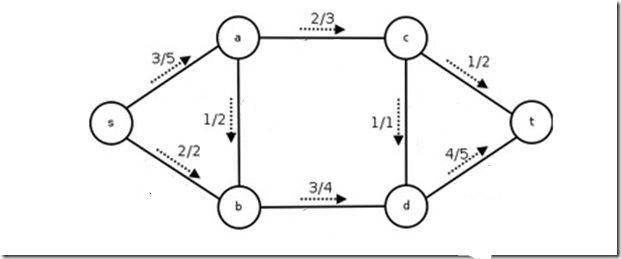
基础表述
请注意:1-12点表述均是建立在有向图上,即未构造反向弧的原图
1.容量网络:设G(V,E),是一个有向网络,在V中指定了一个顶点,称为源点(记为Vs),以及另一个顶点,称为汇点(记为Vt);对于每一条弧<u,v>属于E,对应有一个权值c(u,v)>0,称为弧的容量.通常吧这样的有向网络G称为容量网络.
2.弧的流量:通过容量网络G中每条弧<u,v>,上的实际流量(简称流量),记为f(u,v);
3.网络流:所有弧上流量的集合f={f(u,v)},称为该容量网络的一个网络流.
4.可行流:在容量网络G中满足以下条件的网络流f,称为可行流.
a)弧流量限制条件: 0<=f(u,v)<=c(u,v);
b)斜对称性:f(u,v) = -f(v,u)
c)平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外).
5.零流:若网络流上每条弧上的流量都为0,则该网络流称为零流.
6.伪流: 如果一个网络流只满足弧流量限制条件(即规则<4a>),不满足平衡条件(即规则<4c>),则这种网络流为伪流,或称为容量可行流.(预流推进算法有用)
7.最大流: 在容量网络中,满足弧流量限制条件,且满足平衡条件并且具有最大流量的可行流,称为网络最大流,简称最大流.
8.最小割定理
在一个连通图中,如果删掉若干条边,使图不联通,则称这些边为此图的一个割集。
在这些割集中流量和最小的一个称为最小割。
最大流最小割定理:一个图的最大流等于最小割(证明略)
9.弧的类型:
a.饱和弧:即f(u,v)=c(u,v);
b.非饱和弧:即f(u,v)<c(u,v);
c.零流弧:即f(u,v)=0;
d.非零流弧:即f(u,v)>0.
10.链:在容量网络中,称顶点序列(u1,u2,u3,u4,…,un,v)为一条链,保证其满足相邻的两个顶点之间有一条弧(包括前向弧和后向弧)
设P是G中一条从Vs到Vt的链,约定从Vs指向Vt的方向为正方向.在链中并不要求所有的弧的方向都与链的方向相同,一条链中可能全是后向弧
a.前向弧:(方向与链的正方向一致的弧),其集合记为P+,
b.后向弧:(方向与链的正方向相反的弧),其集合记为P-.
注意:后向弧与反向弧不是一回事
11.增广路:设f是一个容量网络G中的一个可行流,P是从Vs到Vt的一条链,若P满足以下条件:
a.P中所有前向弧都是非饱和弧.(即各弧当前流量小于容量)
b.P中所有后向弧都是非零弧.(稍后解释)
则称P为关于可行流f的一条增广路.
沿这增广路改进可行流的操作称为增广.
增广:
a.前向弧流量加上链的可行流量
b.后向弧流量减去链的可行流量
(可行流量,最大的,并且链上所有前向弧流量加上可行流量小于等于容量,后向弧减去可行流量大于等于0)
注意此处的增广路与下文所述增光路径有差别
12.残留容量:残留容量的定义为:cf(u,v)=c(u,v)-f(u,v)。而由所有属于G的边的残留容量所构成的带权有向图就是G的残留网络。
我们不妨先思考一下增广路的意义何在,请观察下图,源点为a,汇点为d:
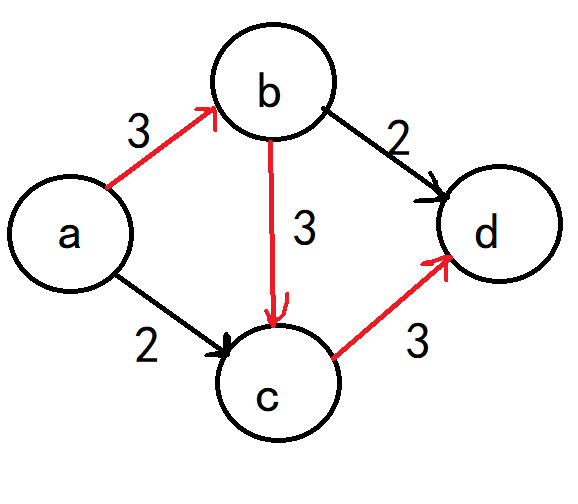
在我们使用贪心思想地去尝试找到最大流的时候,找到一条如图为红色的有向路径,a->b->c->d,它的流量是3,看似这是正确答案
但实际上,最大流是5(a->b为3,a->c为2,b->c为1,c->d为3,b->d为2)
问题何在?我们分析一下,a->c->d最优策略是a->c为2,b->c为1,这样c->d才能物尽其用。但是我们在b处贪心的时候,并没有顾及c的感受,塞了3给它,并且b自己b->d无法又满足
我们在进行贪心的时候我们无法进行真正的最优抉择,或者说,进行了贪心后我们无法悔改
所以后向弧的存在意义就在这里,它通过逆行给予了悔改的机会
同样是刚刚的贪心过程,我们找到了这条红色的路径,显然根据定义,它是一条增广路,他有三条前向弧
而这个时候在链a->c->b->d中
(1)a->c和b->d均是前向弧并且流量小于容量
(2)b->c是后向弧并且f(b,c)=3
所以,a->c->b->d也是一条增广路,可进行增广操作
进行这次增广,我们发现f(b,c)=1,
这也就是说,我们通过逆行悔改使得之前b->c流量成了1,让之前贪心的选择更加理想了
更清晰的处理
实际算法中,我们的搜索是沿有向边方向进行的(无论是dfs还是bfs),后向弧处理起来比较麻烦
所以,我们为了更加清晰的表示,我们需要显化后向弧,故引入反向弧和增广路径概念
以下13、14均表述在建立了反向弧的图上
13.反向弧
在原有的有向弧<u,v>直接添加一条与之反向的弧<v,u>,<v,u>初态为,容量为0,流量为0
这样一来原图就成了双向图

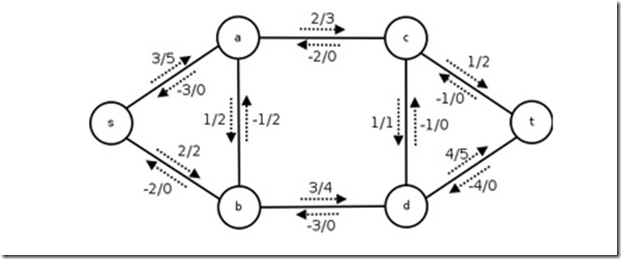
(图中有一处错误b->a应为:-1/0)
14.增广路径以及增广操作
思想基本与上面相同,即每次从源点出发找到一条到达汇点的可行路径,那么从源点到汇点的网络流至少可以增加w(w为这条路径上所有边中的最小残存容量)。
注意这里路径上每条弧均是前向弧(因为后向弧已经被显化成了有向弧)
此时,将最大流增加w,这条路径称为增广路径。
而增广路径上所有弧的流量都加上w,并将每条弧对应的反向弧流量减去w。这个操作就为增广操作。
不断的进行增广操作,直到无法从源到达汇而止。那么,我们就获得了最大流的流量。同时,也可以确定每条边上的流量分布情况
核心思想Ford-Fulkerson
Fold-Fulkerson方法核心就是上述的增广路径思想,只不过效率感人。
为了追求优化,这里介绍四种算法,分别是EK,Dinic,ISAP,HLPP
前三种是基于FF思想,寻找增广路径,而后者则不是,它是基于点的高度进行流量的推送
在增广操作中我们要对互为反向的弧进行流量的修改,便于对他们的访问,四种算法采用的建图方式均为链式前向星
初始化要注意的点:源点的流量为INF
EK(Edmonds-Karp,SAP)
复杂度:O(N * M^2)
思路
为了减少反悔逆行的次数,每次在寻找增广路时,Ek算法利用广搜寻找弧数最少的增广路径,使得进行反悔的次数尽可能的少
代码(hdu1532)
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 205
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
//链式前向星存图
struct Edge
{
int u;
int v;
int cap;
int flow;
Edge(int a,int b,int c,int d){u=a;v=b;cap=c;flow=d;}
};
vector<Edge>edge;
vector<int>G[maxn];
int asc[maxn];//记录改进量
int path[maxn];//记录到这点是来自哪条弧
void init()
{
edge.clear();
for(int i=0;i<maxn;i++)G[i].clear();
}
int cout_flow(int s,int t)
{
int flow=0;
while(1)
{
int curflow=0;
queue<int>node;
memset(asc,0,sizeof(asc));
asc[1]=INF;//注意初始化
node.push(s);
while(!node.empty())//BFS
{
int curpos=node.front();node.pop();
for(int i=0;i<G[curpos].size();i++)
{
int next=edge[G[curpos][i]].v;
int e=G[curpos][i];
if(!asc[next]&&edge[e].cap>edge[e].flow)
{
asc[next]=min(edge[e].cap-edge[e].flow,asc[curpos]);
path[next]=e;
node.push(next);
}
}
}
curflow=asc[t];
if(!curflow)break;//零流跳出循环
flow+=curflow;
for(int i=t;i!=s;i=edge[path[i]].u)//进行增广操作,更新流量
{
edge[path[i]].flow+=curflow;
edge[path[i]^1].flow-=curflow;
}
}
return flow;
}
int main()
{
int m,n,x,y,z;
while(cin>>m>>n)
{
init();
for(int i=0;i<m;i++)
{
cin>>x>>y>>z;
edge.push_back(Edge(x,y,z,0));
edge.push_back(Edge(y,x,0,0));
G[x].push_back(edge.size()-2);
G[y].push_back(edge.size()-1);
}
cout<<cout_flow(1,n)<<'
';
}
return 0;
}
Dinic(多路增广)
复杂度上界O( N^2 * M)
思路
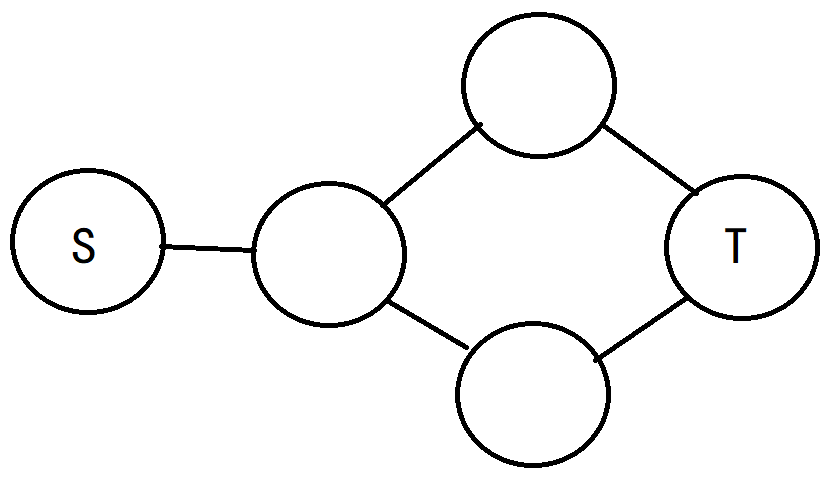
像上图这样EK要进行两次彻头彻尾的BFS
而Dinic以EK算法为基础,它进行了优化--多路广增,
先通过从源点进行BFS打上深度标记,接下来通过DFS寻找多条可行的增广路径
注意:Dinic要求多次BFS,直到无路径可到汇点为止
代码 洛谷P3376
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 200005
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
struct Edge//链式前向星
{
int u;
int v;
int cap;
int flow;
Edge(int a,int b,int c,int d){u=a;v=b;cap=c;flow=d;}
};
vector<Edge>edge;
vector<int>G[maxn];
int dis[maxn];//分层标记
int path[maxn];
void init()
{
edge.clear();
for(int i=0;i<maxn;i++)G[i].clear();
}
bool bfs(int s,int t)//BFS 进行分层操作
{
queue<int>node;
memset(dis,-1,sizeof(dis));
dis[s]=0;
node.push(s);
while(!node.empty())
{
int curpos=node.front();node.pop();
for(int i=0;i<G[curpos].size();i++)
{
int e=G[curpos][i];
int next=edge[e].v;
if(dis[next]==-1&&edge[e].cap>edge[e].flow)
{
dis[next]=dis[curpos]+1;
node.push(next);
}
}
if(dis[t]!=-1)break;
}
if(dis[t]!=-1)return 1;
return 0;
}
int dfs(int s,int t,int flow)//多路增广,flow表示s点处剩余可分配的流量
{
if(s==t||!flow)return flow;
int sum=0;//s点处已经支配出去的流量有多少
for(int i=0;i<G[s].size();i++)
{
int e=G[s][i];
int next=edge[e].v;
if(dis[s]+1==dis[next]&&edge[e].flow<edge[e].cap)
{
int w=dfs(next,t,min(flow,edge[e].cap-edge[e].flow));
//计算若选择这条边e,那么他支配出去的流量有多少
edge[e].flow+=w;
edge[e^1].flow-=w;
flow-=w,sum+=w;//更新s点处剩余流量和已支出的流量
}
if(flow<=0)break;
}
return sum;
}
int Dinic(int s,int t)
{
int ans=0;
while(bfs(s,t))
{
ans+=dfs(s,t,INF);//注意源点可支配的流量是无限的
}
return ans;
}
int main()
{
int m,n,x,y,z,s,t;
cin>>n>>m>>s>>t;
init();
for(int i=0;i<m;i++)
{
cin>>x>>y>>z;
edge.push_back(Edge(x,y,z,0));
edge.push_back(Edge(y,x,0,0));
G[x].push_back(edge.size()-2);
G[y].push_back(edge.size()-1);
}
cout<<Dinic(s,t)<<'
';
return 0;
}
优化(这里我也没懂,当作是玄学优化吧~)
经过优化后复杂度为O(N * M * logC),其中C指的是最大的容量(证明?不会)
核心:伸缩操作
具体做法:
1)将所有边按照其容量二进制下的位数从大到小排序,位数相同的合并成一段。
2)自大到小枚举每一段,在残量网络中加入这一段所有的边,跑一次(普通的)Dinic,将新增广的流量加入答案
ISAP(Improved Shortest Augmenting Path)
复杂度上界O( N^2 * M)
相比Dinic,ISAP算法不需要多次BFS进行分层,而是在DFS回溯的过程中就进行了节点的重标号(即重新分层的操作)。
也就是说ISAP,只需要进行一次BFS
步骤
1.定义dist[v]为点v到达汇点的距离(即经过几个点到达汇点)
2.反向BFS,注意与Dinic的差别
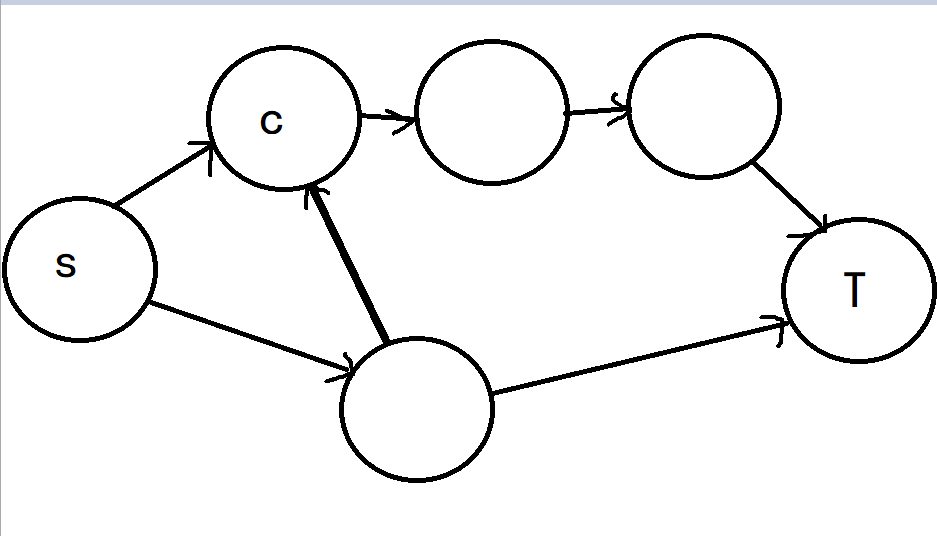
从汇点到源点进行反向BFS,标记下每个节点到达汇点的最短距离,即和Dinic算法相反的分层操作。
一定要取原弧进行操作
像下图,dist[c]应该是3,在反向BFS中很容易误处理成2
3.记录当前点为u。u从源点出发
4.DFS
(1)若点u为汇点,则找到了一条增广路径,进行增广操作,并将u重新放在源点s
(2)若点u可以向前走到v,且u–>v为一条可行边(dist[u] == dist[v]+1,且边u–>v流量不为0),则u走到v
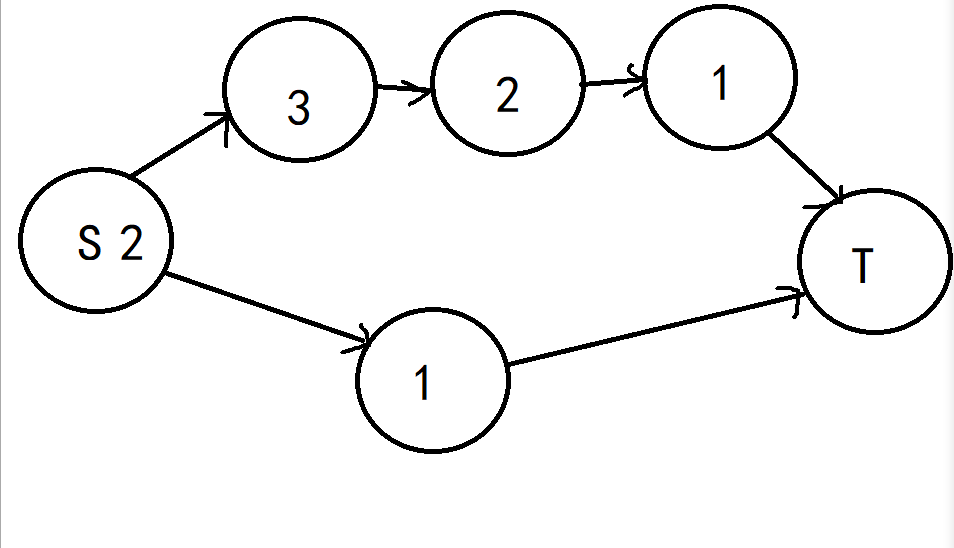
(3)若u无法向前推进到任何点,则对u进行重标号,然后回溯u到原来的增广路径中上一个点pre[u](若为源点不动).
重标号的意义在于下图,S原标号为2,重编号为4
ISAP的优化
GAP优化
Gap[d]在当前残余网络中到达汇点(经过路径上流量不能为0)距离为d的点的个数。
若从u无法找到一条可行边,则表明可以经过dist[u]条边到达汇点的点数目少了一个,即Gap[dist[u]]--。
若此时Gap[dist[u]]==0,则说明当前残余网络中,没有任何一个点可以经过dist[u]条边到达汇点
1)源点到汇点的距离大于等于dist[u],若存在增广路径,那么增广路径上肯定有一点距离为dist[u],矛盾
2)源点到汇点的距离小于等于dist[u],这类情况不存在,由于分层的优先关系,dist越小肯定越先进行搜索,在重编号后,其情况又成为了情况1
综上所述,只要Gap[dist[u]]==0,则可以结束搜索返回值了
当前弧优化
cur[i]用于记录当前点i遍历起始访问弧,它减少了dfs中无意义的访问
注意在给某点重标号的时候,要将该点的cur[i]归零
代码 洛谷P3376
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 200005
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
struct Edge //链式前向星
{
int u;
int v;
int cap;
int flow;
Edge(int a,int b,int c,int d){u=a;v=b;cap=c;flow=d;}
};
vector<Edge>edge;
vector<int>G[maxn];
int dist[maxn];//反向bfs建立距离标号
int pre[maxn];//记录增广路径,当前点是由哪条弧来的
int Gap[maxn];//记录距离为i的点的数量为多少
int cur[maxn];//记录当前各点起始访问弧(从哪个弧开始遍历)
int m,n;
void init()
{
edge.clear();
for(int i=0;i<maxn;i++)G[i].clear();
}
void bfs(int s,int t)//从汇点开始BFS进行距离标记
{
memset(dist,-1,sizeof(dist));
memset(Gap,0,sizeof(Gap));
queue<int>Q;
Q.push(t);
dist[t]=0;
Gap[0]++;
while(!Q.empty())
{
int x=Q.front();Q.pop();
for(int i=0;i<G[x].size();i++)
{
int e=G[x][i]^1;//注意这里一定要取原弧
int next=edge[e].u;//对应弧起点
if(dist[next]==-1&&edge[e].flow<edge[e].cap)//后面这个限制条件也是为了取原弧
{
dist[next]=dist[x]+1;
Gap[dist[next]]++;
Q.push(next);
}
}
}
}
int renew(int s,int t)//当搜索到了增广路径,进行流量更新
{
int curflow=INF;
for(int i=t;i!=s;i=edge[pre[i]].u)//找可行量
{
int e=pre[i];
curflow=min(curflow,edge[e].cap-edge[e].flow);
}
for(int i=t;i!=s;i=edge[pre[i]].u)//增广操作
{
int e=pre[i];
edge[e].flow+=curflow;
edge[e^1].flow-=curflow;
}
return curflow;
}
int isap(int s,int t)
{
bfs(s,t);
int ans=0,u=s;//u表示当前点
memset(cur,0,sizeof(cur));
while(dist[s]<n)
{
if(u==t)
{
ans+=renew(s,t);
u=s;
}
bool ok=0;
for(int i=cur[u];i<G[u].size();i++)//cur[u]是优化,记录遍历
{
int e=G[u][i];
int next=edge[e].v;
if(dist[u]==dist[next]+1&&edge[e].cap>edge[e].flow)
{
ok=1;
pre[next]=G[u][i];
cur[u]=i;//记录节点u访问到哪一条弧了,下次接着访问
u=next;//前进到下一个点
break;
}
}
if(!ok)//节点u找不到可行弧,回退
{
int d=n-1;
for(int i=0;i<G[u].size();i++)
{
int e=G[u][i];
if(edge[e].cap>edge[e].flow)
{
d=min(d,dist[edge[e].v]);
}
}
if(--Gap[dist[u]]==0)break;
dist[u]=d+1;
Gap[dist[u]]++;
cur[u]=0;
if(u!=s)u=edge[pre[u]].u;
}
}
return ans;
}
int main()
{
int x,y,z,s,t;
init();
cin>>n>>m>>s>>t;
for(int i=0;i<m;i++)
{
cin>>x>>y>>z;
edge.push_back(Edge(x,y,z,0));
edge.push_back(Edge(y,x,0,0));
G[x].push_back(edge.size()-2);
G[y].push_back(edge.size()-1);
}
cout<<isap(s,t)<<'
';
return 0;
}
HLPP(预流推进,推送-重贴标签)
复杂度上限O(N^2 * M^(1/2) )
开篇废话
网上代码写的五花八门,而且是各种玄学优化过的版本(而且各种缩写看的让人不知所措...),存图也是各类都有...
黑书上说这个算法算是最大流最快的算法,
原话:到目前为止,许多渐近效率很高的最大流算法都是推送-重贴标签算法
在稠密图中预流推进效率明显更高,明显强于其他增广路算法
思路
存图:链式前向星(可以优化,后面再谈)
在所有的增广路算法中,我们引入反向边的意义在于对交叉路径的选择提供了一种反悔的可能
而增广操作,是一种保守的增流方式

而实际上像上图中,我们为a->b,a->c,b->d,c->d都构造了反向边,却没有实际用处,如果我们能让他们也能被利用起来,让他们也有能反悔的机会,那么增流效率能大大提高
预流推进的思路正基于此,它是一种激进的增流方式。
形象点说,我先不管你能不能吃得下,我先塞到你嘴里,你发现咽了一部分,发现还有一部分下不去,就吐回来给我
而增广的思路是吃多少喂多少,合理取食
在稠密图中,增广路算法需要花费大量时间在两件事上,一是找增广路,二是走一遍增广路更新,如果在稠密图中,路径太多,交叉频率太大,反悔的次数大大增多,找一遍,跑一遍,性能大打折扣
而预流推进算法不同,它强调的推流对象是各个节点,性能大大的好
核心
1)与ISAP一样,进行反向BFS,预处理每个点的高度dist
2)伪流&超额流(余流)
伪流上面术语部分介绍过了,通俗理解就是每条弧都是充满流量地传递,不顾受者情况
而超额流指的就是当前节点所含的流量,要将每个点(非源点、非汇点)的超额流全部推送出去,才能真正形成可行流
3)推送
高度的作用就是为了给推送一个方向,而每次推送选择的弧均满足:
a)两点高度降一
b)边的剩余可推流量非零
c)当前节点超额流非0
4)推送次序
使用以高度为键值的大根堆(优先队列),只要该节点(非源点汇点)它还有超额流,就要进行流量的推送
5)重贴标签
当前节点没有可行弧进行推送,并且它有额外流,则它需要改变当前高度,使得自己能有可行点去推送,并且这个高度越小越好,这一过程即为“重贴标签”
注意重贴标签的过程中可能把某个点的高度抬高,也有可能把某个点的高度降低
优化点
1)邻接表存图
常规邻接表有邻点,边权(流量)
这里额外存储一个vis
它表示反向弧在以v为起点的邻接表中标号为多少
这样,就便于直接访问反向弧了,而不需要前向星去存边了
2)Gap优化
数组Gap与ISAP中用于优化的Gap一样,都是记录某个高度有多少节点,但是终止条件改变了
注意Gap值仅仅表示某个高度的点的数量有多少,与余流无直接关联
我们是在重标签过程中去改Gap值的(因为重标签改变了高度,间接改变了Gap值)
所以当前改变了Gap值的点应该是有余流且高度最大的(基于优先队列的选择)
一旦某个高度对应的Gap值为0,接下来对于当前点而言,它有两种选择:
(1)因为自己现在是高度最大的且有余流,所以在重标签的过程中它降低高度,将流尽可能的往低处推
(2)比他高度大的点均无余流(优先队列的原则),所以它发现一旦无法将自身余流往低处推送,那么他只能抬高往源点回传
所以为了加快第二步,一旦出现断层,我们就将比当前断层高度高的所以点全抬到n+1,使得他能尽可能快地将流往高度为n的源点推送
3)重贴标签优化
在进行推流的时候我们遍历了一次某个点的邻接表
如果它还有额外流,那么它为了找可行推流的高度,又要遍历一次
所以不妨推流的时候顺带记录一下,减少无意义的遍历
4)using namespace std的优化
真的很迷
很多时候STL跑起来慢,但是把using namespace std删了,改成std::这样的东西,再把O2点上,快好多
注意点
1)注意像下图,点4这种,它到汇点无路径
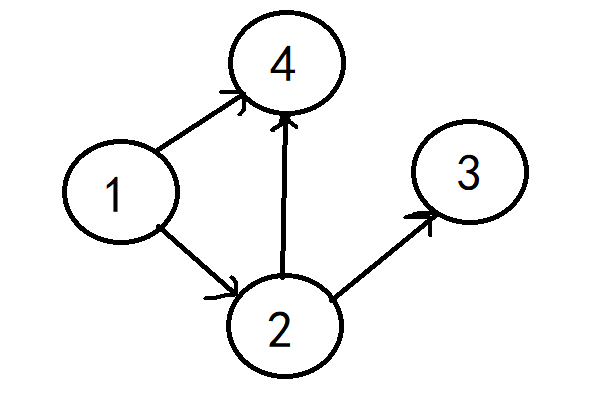
增广路算法中可以回避这个问题,而预流推进中必须防止将流向点4这样dist==INF的点去推(尤其要注意从1开始推的时候)
2)很多题目写明最大流答案不超过2^32,但是你仍然需要开long long
增广路径算法不考虑这个问题,但预流推进中超额你不知道它可能会超多少,推进过程中超额流可能会产生数据溢出,就会直接TLE
3)Gap要开的足够大,因为Gap是记录某一高度的数量,高度很容易在重贴标签的过程中被莫名抬高,没开够很容易在大数据下RE
洛谷P4722 最高标号预流推进模版 优化版
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
#define INF 0x5f5f5f5f
#define maxn 1305
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
inline int read()
{
int ans=0;
char last=' ',ch=getchar();
while(ch<'0'|ch>'9')last=ch,ch=getchar();
while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
if(last=='-')ans=-ans;
return ans;
}
int dist[maxn];//记录高度
ll e[maxn];//注意要用long long 来记录超额流
int Gap[maxn<<2];//这里Gap一定要多开一点
bool exi[maxn];//记录当前优先队列是否存在某个元素,一定记得源点汇点不入队
int m,n,s,t;
//这里摈弃了链式前向星,使用邻接表记录,注意vis的含义
struct ed
{
int v;//弧的终点
ll flow;
int vis;//指反向弧在以v为起点的邻接表中标号为多少,记录这便于直接访问反向弧
ed(int a,ll b,int c):v(a),flow(b),vis(c){}
};
std::vector<ed>G[maxn];
void init()//初始化,注意memset对非0的初始化一定要写成0x...
{
for(int i=0;i<maxn;i++)G[i].clear();
memset(Gap,0,sizeof(Gap));
memset(exi,0,sizeof(exi));
memset(dist,INF,sizeof(dist));
for(int i=0;i<=n;i++)e[i]=0;
}
struct cmp//重载cmp,定义以dist为键值的大根堆
{
bool operator () (int a,int b)
{
return dist[a]<dist[b];
}
};
std::priority_queue<int,std::vector<int>,cmp>heap;
void add_edge(int u,int v,int w)//注意如何添加弧以及记录vis的值
{
G[u].push_back(ed(v,w,G[v].size()));
G[v].push_back(ed(u,0,G[u].size()-1));
}
ll min(ll a,ll b)
{
return a<b?a:b;
}
bool bfs()//反向bfs标记,与ISAP相同,但注意如果某点不能到汇点,它的高度应该是INF
{
std::queue<int>Q;
Q.push(t);
dist[t]=0;
int a;
while(!Q.empty())
{
int x=Q.front();Q.pop();
for(int i=0;i<G[x].size();i++)
{
int v=G[x][i].v;
if(dist[v]==INF&&!G[x][i].flow)
{
dist[v]=dist[x]+1;
Q.push(v);
}
}
}
if(dist[s]==INF)return 0;
return 1;
}
void push(int u)//推流操作,只能往高度矮1的节点推流,以及这里进行了优化,将重标签的过程并入
{
int height=INF,cur=0;
for(int i=0;i<G[u].size();i++)
{
cur=i;
int vis=G[u][i].vis;
int v=G[u][i].v;
if(dist[v]==INF)continue;
if(G[u][i].flow&&dist[u]==dist[v]+1&&e[u])
{
int curflow=min((ll)G[u][i].flow,e[u]);
e[v]+=curflow,e[u]-=curflow;
G[u][i].flow-=curflow;
G[v][vis].flow+=curflow;
if(v!=s&&v!=t&&!exi[v])
{
heap.push(v);
exi[v]=1;
}
}
else
{
if(G[u][i].flow)height=std::min(height,dist[G[u][i].v]+1);
}
if(!e[u]&&height!=INF)break;
}
if(e[u])
{
Gap[dist[u]]--;
if(!Gap[dist[u]])//出现了Gap断层的优化
{
for(int i=1;i<=n;i++)
if(dist[i]>dist[u]&&dist[i]<n+1&&i!=s&&i!=t)
dist[i]=n+1;
}
for(int i=cur;i<G[u].size();i++)
if(G[u][i].flow)height=std::min(height,dist[G[u][i].v]+1);
if(height!=INF)
{
dist[u]=height;
Gap[height]++;
}
}
}
ll hlpp()
{
if(!bfs())return 0;
dist[s]=n;
for(int i=1;i<=n;i++)//计算Gap数组
if(dist[i]!=INF)Gap[dist[i]]++;
for(int i=0;i<G[s].size();i++)//暴力将源点的推出去,再将源点抬高到n
{
int vis=G[s][i].vis;
int v=G[s][i].v;
int curflow=G[s][i].flow;
if(dist[v]==INF)continue;
e[v]+=curflow,e[s]-=curflow;
G[s][i].flow-=curflow;
G[v][vis].flow+=curflow;
if(v!=s&&v!=t&&!exi[v])
{
heap.push(v);
exi[v]=1;
}
}
while(!heap.empty())
{
int x=heap.top();
heap.pop();exi[x]=0;
push(x);
if(e[x])
{
heap.push(x);exi[x]=1;
}
}
return e[t];
}
int main()
{
int x,y,z;
init();
n=read(),m=read(),s=read(),t=read();
for(int i=0;i<m;i++)
{
x=read(),y=read(),z=read();
if(x==y)continue;
add_edge(x,y,z);
}
e[s]=INF<<1;
std::cout<<hlpp()<<'
';
return 0;
}