相似矩阵
定义
特征值的一个重要应用是,他能将A进行对角化,得到:( Lambda =S^{-1}A S )(假如存在S逆的话)。如果我们将S替换为一般的矩阵M(存在逆矩阵),得到:( B=M^{-1}AM ),我们说B与A相似(当然A与B也相似,相似是相互的)。当然,A与Λ是相似的。
相似矩阵的特征值相同
为什么要讨论相似矩阵?因为我们要带出一个重要结论:相似矩阵的特征值相同(但特征向量不同,见下)。
证明很简单:
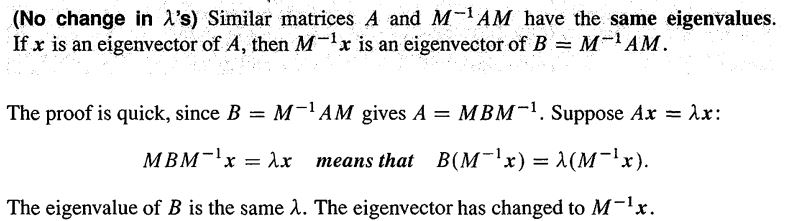
- 对角矩阵应该是相似矩阵中的明星,因为它的特征值就在对角线上,特征向量是(1,0),(0,1)(拿二维打个比方)
- 上三角矩阵也是重要一员,它的特征值也在对角线上,不过它的特征向量没这么容易看出来。
当A的特征值相同时
美好的愿望:我们似乎能将相似矩阵归为一个大family,family中的矩阵两两之间相互相似(拥有相同特征值),可以通过Λ将他们连接起来。我们可以证明相似的传递性:
假设( B=M^{-1}Lambda M ),( C=N^{-1}Lambda N ),
那么( C=N^{-1}MLambda M^{-1}N=(M^{-1}N)^{-1}Lambda (M^{-1}N) ),证毕。
残酷的现实:遗憾的是,当集合中特征值相同时,具有相同特征值的矩阵集合这个大family分为两个小family:
- 其一只包含对角矩阵:λI
- 其二是其余所有矩阵,一个代表是上三角矩阵,对角线元素是λ,上三角随便填什么数都行
这两个family有以下特点:
- 第一个矩阵永远无法与第二族矩阵相似,第一个矩阵只能与他自己相似,因为对任何M,都有M-1λIM=λI
- 第二个family中的矩阵无法对角化(假如能对角化,它们就需要与第一个矩阵相似,这是不可能的)
Jordan form与Jordan matrix

当矩阵所有特征值相同时,将上三角紧贴对角线的元素以1填充,得到的矩阵叫做Jordan form,由这些Jordan form在对角线上构成的矩阵叫做Jordan Matrix(见图)。
- Jordan Matrix的特征向量个数=块的个数(因为每个块内特征值相同,带出的特征向量也相同)
- 可以证明任何方阵A都与某个Jordan Matrix相似(这个证明,以及给出A求Jordan Matrix的过程都不容易,此处略过)
- 如果矩阵没有重复的特征值,那么Jordan Matrix退化为对角矩阵Λ,这也是我们所期望的结果。