一、数列与数列极限
刘徽——割圆术
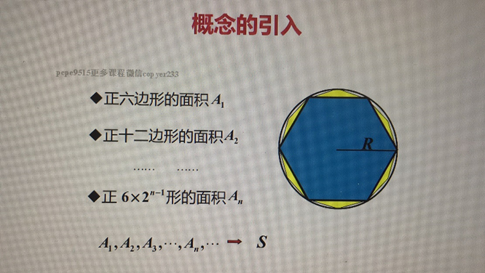

还可以表示为 xn= 1- 1/(2^n)
因为棒长是固定1 减去最后一天剩下的 也是截取的总长
1-1/(2^n)无限趋近于1
数列的定义
·按自然数1,2,3,…编号依次排列的一列数 x1 x2 … xn … 称为无穷数列 简称数列
·其中每个数称为数列的项,xn称为通项(一般项) 此数列可记为{xn}
例如 2 4 8 …2^n… {2^n}
问题
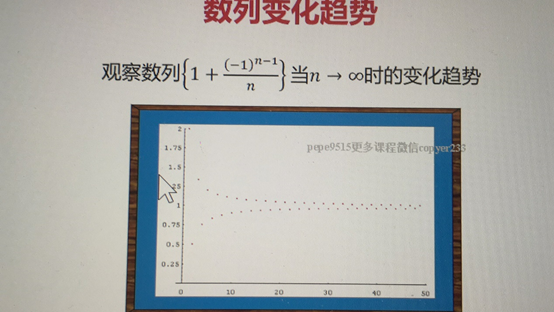
·当n无限增大时 xn是否无限接近某一确定的数指
上面实验 当n无限增大时 数列{1+ ( (-1)^(n-1) )/n
问题
·无限接近意味着什么 如何用数学语言刻画它

数列的极限
·如果对于任意给定的正数e(不论它多么小)
·总存在正整数N,
·使得对于n>N时的一切xn
·不等式|xn-a|<e都成立,
那么就称常数a是数列xn的极限 或者称数列xn收敛于a
记为lim n->∞ xn = a (或xn ->a(n->∞))
注意
·注1:如果数列没有极限,就说数列是发散的(不收敛的
·注2:不等式|xn-a|<e 刻画了xn与a无限接近
·注3:定义中正整数N与任意给定的正数e有关
数列极限的几何解释
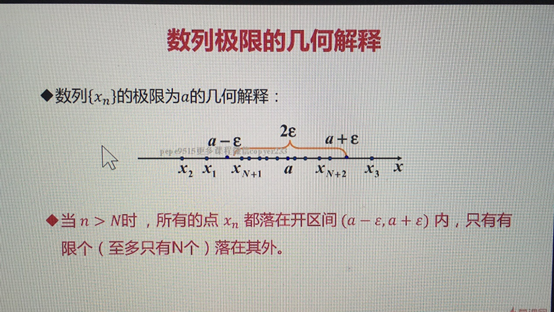
将a表示出来 然后做a的邻域
当n>N的时候,所有的点都会落入到橘黄色的开区间内 只有有限个(至多有N个 不大于大N的)落在其外
e-N语言
任意符号(把A倒置过来
存在符号(把E反转过来
·数列极限定义并未给出求极限的方法
例题1:

例题2:

例题3:

数列的极限
·如果对于任意给定的正数 (不论它多么小)
·总存在正整数N,
·使得对于n>N时的一切xn
·不等式|xn-a|<都成立,
那么就称常数a是数列xn的极限 或者称数列xn收敛于a
记为lim n->∞ xn = a (或xn ->a(n->∞))
二、收敛数列的性质
收敛:有极限
发散:无极限
收敛数列的性质:
1.有界性
·对数列xn 若存在正数M
·使得一切自然数n 恒有|xn|<M成立
则称数列xn有界,否则,称为无界
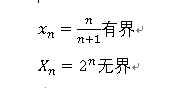
有界
无界
定理一 收敛的数列必定有界
证明: 
由定义,取
则 使得当n>N时 恒有|xn-a|<1 即有a-1<xn<a+1
记M= max{|x1|,…,|xn|,|a-1|,|a+1|}
则对一切自然数n,皆有|xn|<M,故{xn}有界
注:有界性是数列收敛的必要条件
2.唯一性
定理2 每个收敛的数列只有一个极限
3.保号性
如果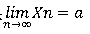
且a>0(或a<0) 那么存在正整数N>0 当n>N时
都有xn>0(或xn<0)
4.收敛数列与其子数列间的关系
如果数列收敛于a,则它的任一子数列也收敛 且极限也是a
4.收敛数列与其子数列间的关系
如果数列收敛于a,则它的任一子数列也收敛 且极限也是a